藍寶石諧振體內的回音壁模電磁場分布*

范思晨 楊帆 阮軍

1) (中國科學院國家授時中心,西安 710600)

2) (中國科學院大學,北京 100049)

3) (中國科學院時間頻率基準重點實驗室,西安 710600)

藍寶石諧振體內的電磁場為回音壁模式時具有極低的介質損耗.本文采用徑向-軸向模式匹配法,理論分析了藍寶石諧振體內的場模式分布,分析了諧振頻率與諧振體幾何尺寸的關系;其次,基于有限元分析仿真了藍寶石圓柱體內場分布情況;研制了三維轉動位移臺,采用磁環/探針耦合的方式激發藍寶石諧振體內的回音壁電磁場,測量了諧振體表面的S 參數,由此確定了諧振體內的回音壁模式參數,得到諧振器的無載Q 值為94000.利用該諧振體可制成低相位噪聲的微波振蕩器.

1 引言

藍寶石諧振體內的電磁場為回音壁模式時具有極低的介質損耗[1],由此制成的振蕩器具有超低相位噪聲和較高中短期頻率穩定度等特性[2,3],在原子頻率標準[4?7]、暗物質探測[8,9]、量子計算[10,11]、甚長基線干涉儀[12,13]和深空探測[14,15]等領域有重要應用.藍寶石諧振體內的電磁場模式與振蕩器品質因子Q存在確定的函數關系[16,17],直接影響著振蕩器的相位噪聲,因此確定藍寶石諧振體內的電磁場分布是實現高性能振蕩器的先決條件.由于回音壁模式的電磁場絕大部分分布在藍寶石內部,并不能直接利用探針測量其分布,一般多采用模式匹配法[18?21],計算特定模式的諧振頻率和藍寶石內部的電磁場分布,或者應用軟件仿真方法來確定電磁場分布,很少進行實驗驗證.

本文設計并研制了裝配雙端磁環/探針的精密轉動位移臺,激勵產生了藍寶石諧振體內的回音壁模式電磁場,同時獲得了藍寶石諧振體外的電磁場分布,通過與模式匹配法理論計算和微波軟件仿真結果進行比較,從而確定了藍寶石諧振體內的回音壁模式電磁場參數.

2 藍寶石諧振體的電磁場模式結構

藍寶石是各向異性的單晶體材料,對于圓柱形藍寶石,它的晶軸(C軸)與z軸平行,平行于晶軸方向的相對介電常數為ε//,垂直于晶軸方向的相對介電常數為εr和εθ.實驗中藍寶石尺寸為直徑54.21 mm,高30.00 mm,藍寶石柱體的一端有一個直徑10.00 mm,高22.00 mm 的小圓柱體用于將藍寶石固定在腔內.在292 K 時,藍寶石的相對介電常數ε⊥=9.39,ε//=11.576.

2.1 理論研究

介質諧振體理論分析方法有介質波導法[22]、徑向模式匹配法[23]、軸向模式匹配法[24],本文采用Tabor 和Mann[19]提出的徑向與軸向結合的模式匹配方法.

徑向匹配得到以下超越方程[25]:

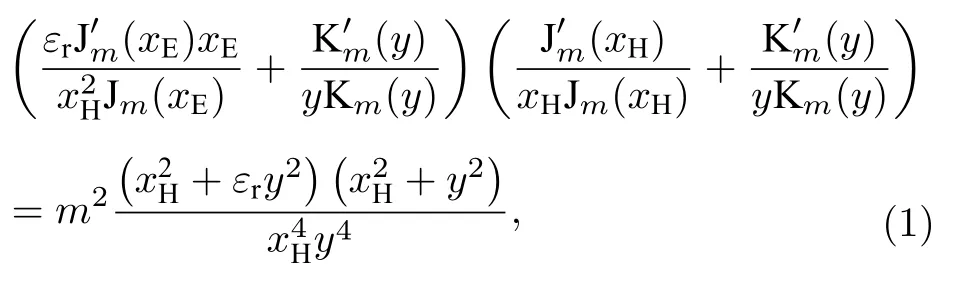
在這里,

其中,Jm為m階第一類貝塞爾函數,Km為m階第二類修正貝塞爾函數,kE是平行于c軸的介質傳播常數,kH是垂直于c軸的介質傳播常數,β是軸向傳播常數,kout是外徑向傳播常數,k0是自由空間波數.

軸向匹配可以得到:

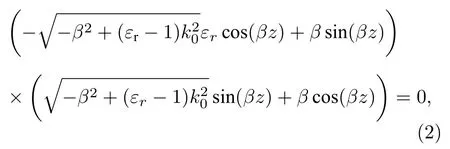
利用上述兩個方程即可求得藍寶石諧振體工作在回音壁模式的諧振頻率.

2.2 藍寶諧振體內的電磁場仿真分析

有限元方法可以仿真藍寶石諧振體內的電磁場分布情況[26?28].利用三維電磁場仿真軟件CST Studio Suite 建立仿真模型,使用本征模求解器仿真藍寶石晶體工作在回音壁模式下的場分布,仿真模型如圖1(a)所示.分別對藍寶石諧振體和空氣區域進行不同的網格剖分,求解數值精度為10–9,迭代次數為6.當藍寶石介質工作在WGH15,0,0模式時,電磁場的能量密度分布如圖1(b)和圖1(c)所示.圖1(b)中,圓柱體為藍寶石柱,外部為空氣,電磁能量被限制在藍寶石晶體邊界靠近空氣的地方,在方位角上呈現花瓣形狀,具有周期性.

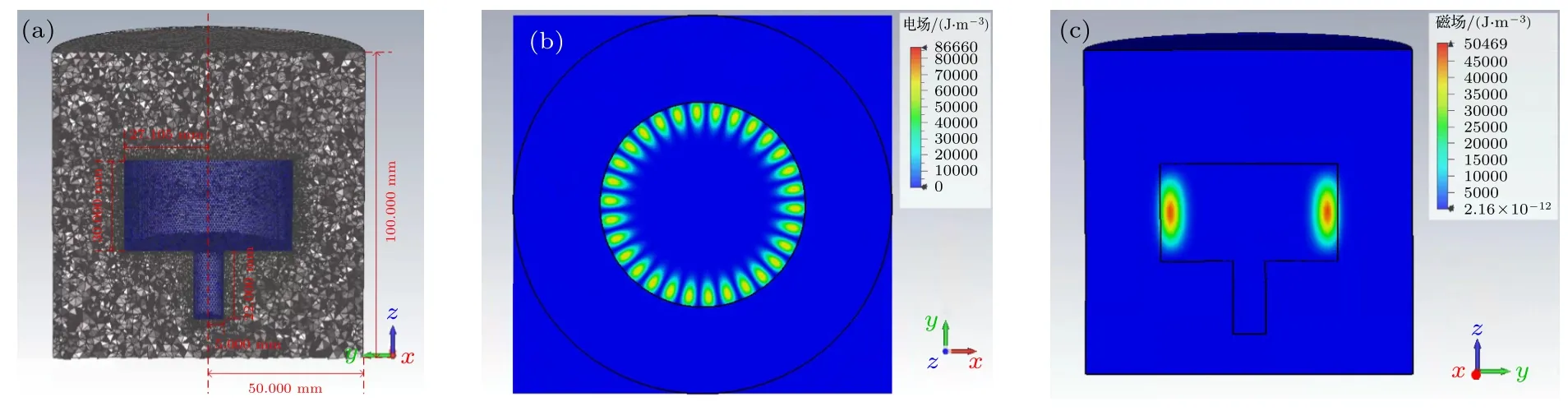
圖1 WGH15,0,0 模式仿真 (a) 有限元模型網格填充剖面圖;(b)電場方位角向分布;(c) 磁場徑向分布Fig.1.WGH15,0,0: (a) Mesh filling section of finite element model;(b) azimuth distribution of electric field;(c) radial distribution of the magnetic field.

2.3 藍寶石諧振體的電磁場分布實驗測量

通過近場探測的方法確定藍寶石柱腔內的微波模式場分布,測試裝置如圖2 所示.

圖2 測量WGH 模式共振頻率裝置示意圖Fig.2.Schematic diagram of measuring WGH mode resonance frequency device.

矢量網絡分析儀作為微波產生和探測的裝置,使用主動型氫鐘作為其時鐘參考.矢量網絡分析儀端口1 發射的微波通過固定的磁環耦合進樣品,在內部和表面形成回音壁模式的諧振器電磁場.用磁環或探針對樣品表面電磁場進行探測,磁環和探針天線通過精密位移臺(分辨率0.01 mm)和轉動臺(分辨率0.01°)固定,接收端可沿軸向(z)、徑向(ρ)和方位角(θ)方向調節.可移動的磁環或天線連接到矢量網絡分析儀端口2 作為微波接收端,測量S參數隨空間的變化情況.調節臂2 的軸向高度,可以確定WGH 模式軸向數;將臂3 探針沿徑向移動,可以確定徑向數;將臂2 繞藍寶石樣品旋轉,觀測S21變化的周期性變化,可以確定方位角數.

3 結果分析和討論

3.1 藍寶石諧振體回音壁模式分析

利用上述測量裝置對WGH15,0,0模近場進行測量,并與有限元仿真電磁場強度絕對值進行對比,如圖3 所示,其中黑線表示有限元仿真法電磁場強度絕對值,紅線表示實驗測量S21值.圖3(a)表示磁場強度方位角向分布,磁環繞方位角方向S21測量值和有限元法的磁場強度絕對值變化趨勢基本符合,在方位角上電磁場強度具有周期性,每12°為一個周期,故m=15 .圖3(b)表示磁場強度軸向分布,磁環位置在軸向上高度變化激勵的S21值與有限元法的磁場強度絕對值較一致,在軸向上p=0.圖3(c)表示電場強度徑向分布,探針位置在徑向上變化激勵的S21值與有限元法的電場強度絕對值趨勢一致,在徑向上電場強度具有對稱性,n=0.

圖3 WGH15,0,0 模式電磁場強度 (a) 磁場強度方位角向分布;(b) 磁場強度軸向分布;(c)電場強度徑向分布Fig.3.Electromagnetic field intensity of WGH15,0,0: (a) Cross-section distribution of magnetic field intensity;(b) axial cross-section distribution of magnetic field intensity;(c) cross-section distribution of electric field intensity diameter.

3.2 藍寶石諧振體諧振頻率分析

實驗中,采用磁耦合方式激發和探測.圖4 中,紅線為通過模式匹配法計算出的WGHm,0,0模式諧振頻率,藍線為有限元分析法得到的WGHm,0,0模式諧振頻率,綠線為實驗測得的WGHm,0,0模式諧振頻率.理論計算、有限元法仿真和實際測量得到的頻率值基本符合.

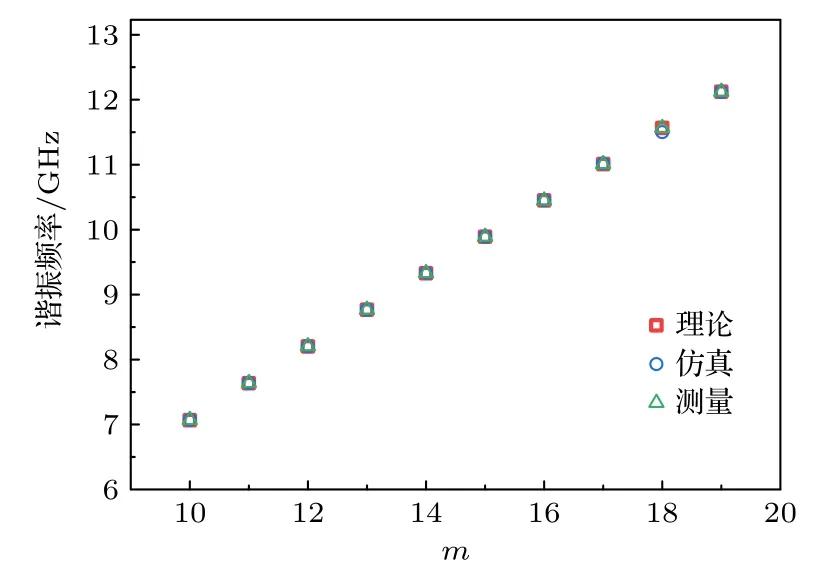
圖4 WGHm,0,0 模式理論頻率和測量頻率的比較Fig.4.Comparison of theoretical and measured frequencies of WGHm,0,0 models.

WGHm,0,0模式測量的諧振頻率與方位角模式數呈線性關系,與理論計算值和有限元分析結果一致.表1 給出理論計算、有限元仿真和實驗測量得到的諧振頻率,并且計算得到精度.分析可得,有限元仿真得到的精度 Δf/f＜0.06%,實驗測量結果得到的精度 Δf/f＜0.02 %.

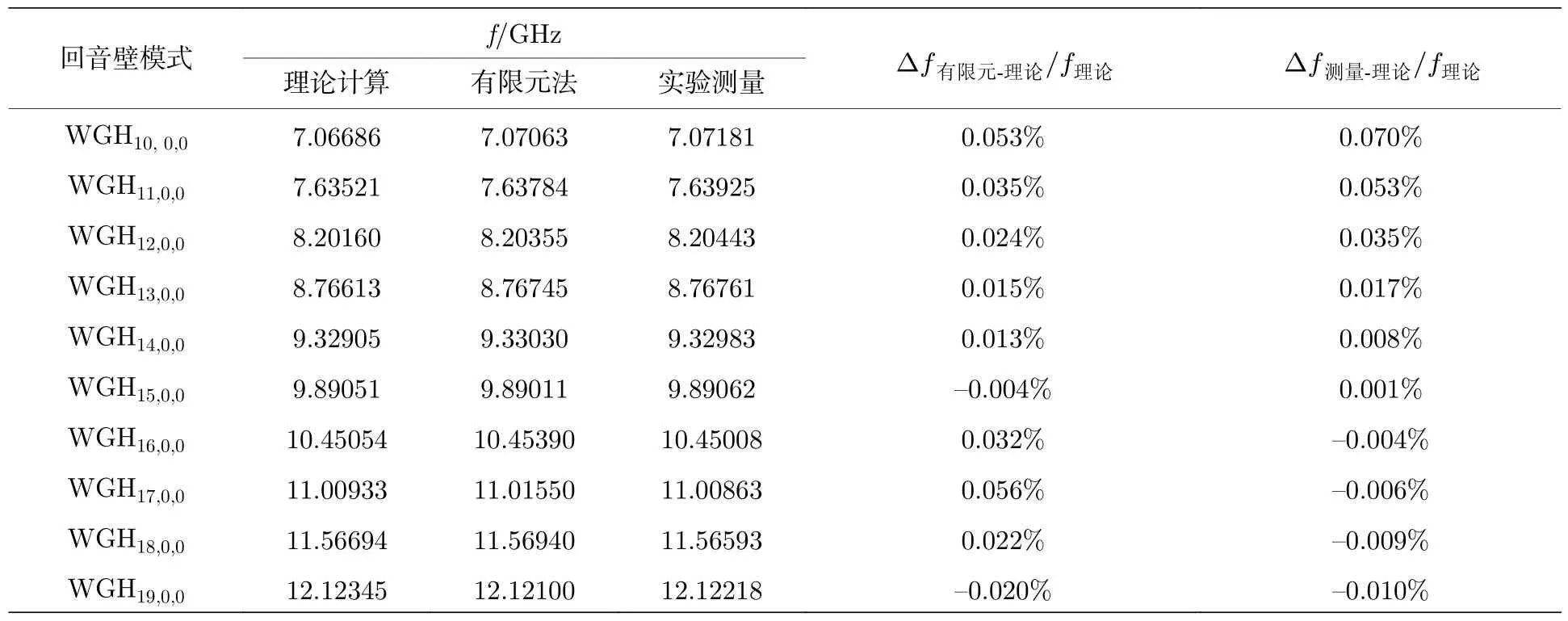
表1 m=10—19 的諧振頻率Table 1.Resonant frequency of m=10–19.

圖5 中,測量帶寬為300 MHz,激發探頭和探測磁環之間的夾角為180°.WGH15,0,0附近存在多個雜散模,在形成振蕩環路時,容易跳頻.圖3中,WGH15,0,0在方位角方向上存在周期性,當激發磁環和探測磁環之間的夾角為180°時,所有模態都被激發.改變可移動磁環在方位角方向上的位置,將其固定在WGH15,0,0最大場位置,此時磁環沿諧振體軸旋轉=12°,激發磁環和探測磁環之間的夾角為168°,WGH15,0,0模式不受影響,且雜散模式被有效抑制,測試結果如圖5 中綠線所示.

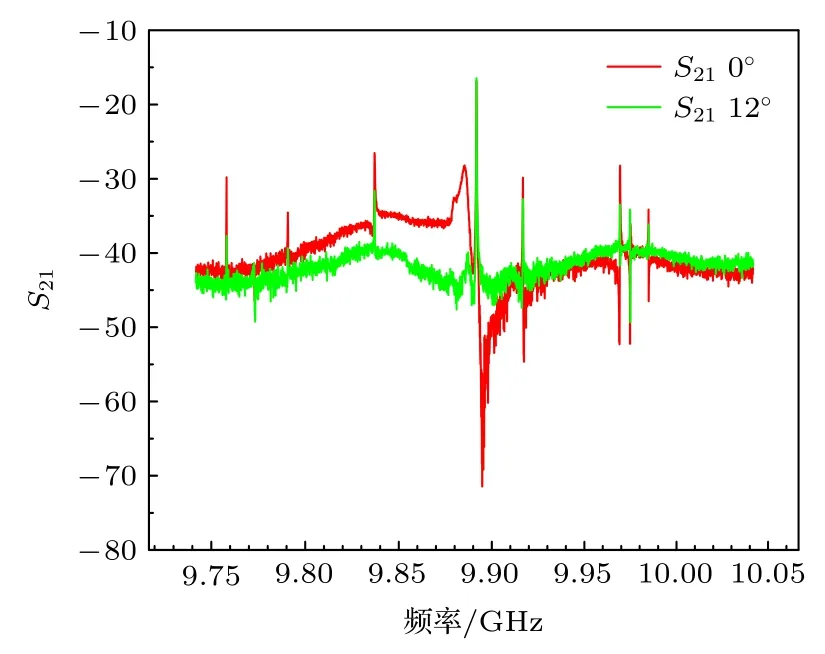
圖5 室溫下WGH15,0,0 模式磁環不同位置的S21 參數Fig.5.S21 at different positions of WGH15,0,0 mode magnetic rings in samples at room temperature.

當激發磁環和探測磁環之間的夾角為168°時,利用矢量網絡分析儀ZVB14 對藍寶石諧振體的S參數進行測量,結果如圖6 所示,測量帶寬為2 MHz.紅線為S12,綠線為S21,其中f0=9891754142 Hz,Δf=124041 Hz,根據QL=可得,QL≈8×104,故Q0=≈9.4×104.

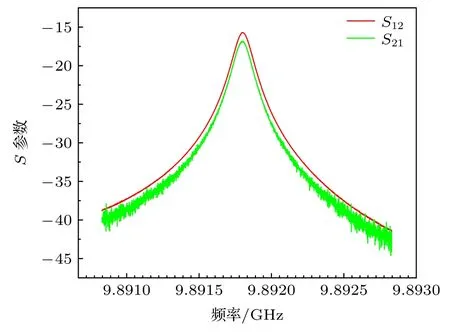
圖6 室溫下樣品的WGH15,0,0 模式S 參數Fig.6.WGH15,0,0 mode S parameters of samples at room temperature.

3.3 諧振腔頻率-溫度敏感度分析

溫度是影響藍寶石諧振體的諧振頻率的主要因素.其頻率-溫度敏感度(TCF)[29]如下:

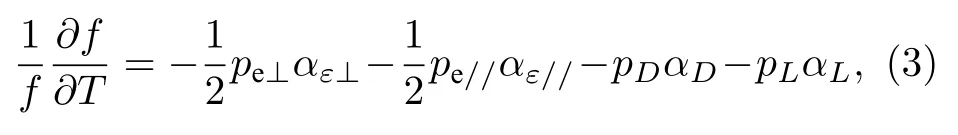
式中,

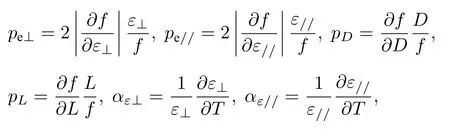
pe⊥和pe//分別為垂直于晶軸方向和平行于晶軸方向的電場填充因子,pD和pL分別為回音壁模式諧振頻率對藍寶石柱直徑和高度變化的敏感度,αε⊥和αε//分別為垂直于晶軸方向和平行于晶軸方向的介電常數溫度系數,αD和αL分別為垂直于晶軸方向和平行于晶軸方向的熱膨脹系數.

分別加入微擾 ΔD和 ΔL,通過模式匹配法和有限元分析法分別求得此時的 Δf.圖7 給出藍寶石諧振體直徑(D)和高度(L)變化對回音壁模式WGH15,0,0諧振頻率的影響.改變藍寶石柱直徑D(mm)得到諧振頻率隨直徑的變化關系,根據pD=可得,pD≈0.973 .保持藍寶石柱直徑不變,改變高度H(mm)得到諧振頻率隨高度的變化關系,根據pL=可得,pL≈0.027.可以看出諧振頻率隨直徑變化的敏感度大于隨高度變化的敏感度.

圖7 WGH15,0,0 諧振頻率與樣品尺寸關系 (a) 諧振頻率與直徑變化的關系;(b) 諧振頻率與高度變化的關系Fig.7.Relationship between resonant frequency and sample size: (a) Relation between resonant frequency and diameter change;(b) relation between resonant frequency and height variation.

分別加入微擾 Δε⊥和 Δε//,通過模式匹配法和有限元分析法分別求得此時的 Δf.圖8 給出了藍寶石回音壁模式WGH15,0,0諧振頻率與相對介電常數的關系.改變藍寶石垂直于晶軸的相對介電常數得到諧振頻率隨ε⊥的變化關系,根據pe⊥=可得,pe⊥≈0.032.保持藍寶石垂直于晶軸的相對介電常數不變,改變平行于晶軸的相對介電常數,得到諧振頻率隨ε//的變化關系,根據pe//=可得,pe//≈0.96 .諧振頻率隨平行于晶軸的相對介電常數變化的敏感度大于隨垂直于晶軸的相對介電常數變化的敏感度.

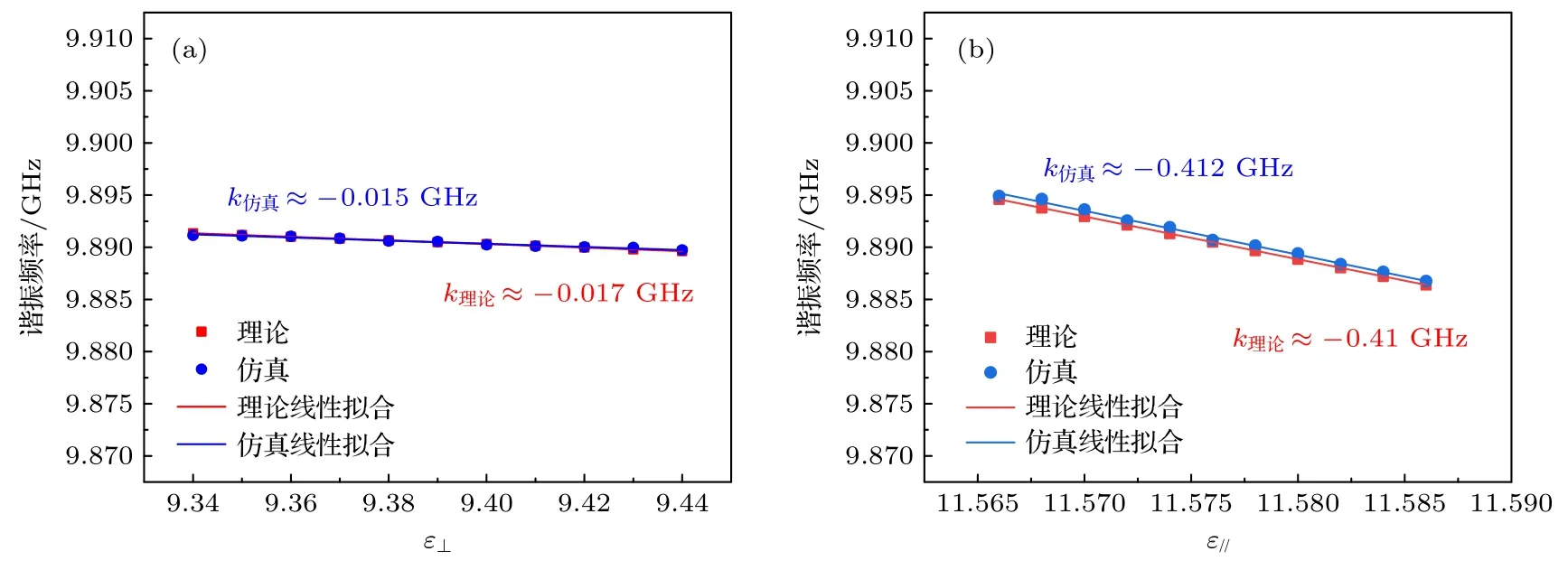
圖8 WGH15,0,0 諧振頻率與相對介電常數的關系 (a) 諧振頻率與 ε⊥ 的關系;(b) 諧振頻率與 ε// 的關系Fig.8.Relation between resonant frequency and relative permittivity: (a) Relation between resonant frequency and ε⊥ ;(b) relation between resonant frequency and ε//.

對于WGH15,0,0模,TCF 近似為結果表明,藍寶石諧振體工作在WGH15,0,0回音壁模式的頻率-溫度敏感度主要與平行于晶軸方向的介電常數溫度系數和垂直于晶軸方向的熱膨脹系數有關.

圖9 給出垂直于晶軸的介電常數和平行于晶軸的介電常數與溫度的關系[30].在低溫下,介電常數對溫度的敏感度小,隨溫度的變化趨勢較緩慢;當溫度升高到一定值時,介電常數對溫度的敏感度逐漸增大,隨溫度的變化趨勢較快.圖9 中藍線表示當溫度為292 K 時加入微擾 ΔT,分別求得此時的 Δε⊥與 Δε//.改變溫度得到介電常數隨溫度的變化關系.根據αε⊥=可得,αε⊥≈91.07×10-6K-1.根據αε//=可得,αε//≈133.03×10-6K-1.

圖9 溫度對相對介電常數的影響 (a) ε⊥ 與溫度的關系;(b) ε// 與溫度的關系Fig.9.Influence of temperature and relative permittivity: (a) Relationship between ε⊥ and temperature;(b) relationship between ε//and temperature.

圖10 給出垂直于晶軸的熱膨脹系數和平行于晶軸的熱膨脹系數與溫度的關系[31].圖中藍線表示在溫度為20—350 K 時,垂直于晶軸的熱膨脹系數和平行于晶軸的熱膨脹系數與溫度關系的擬合曲線:

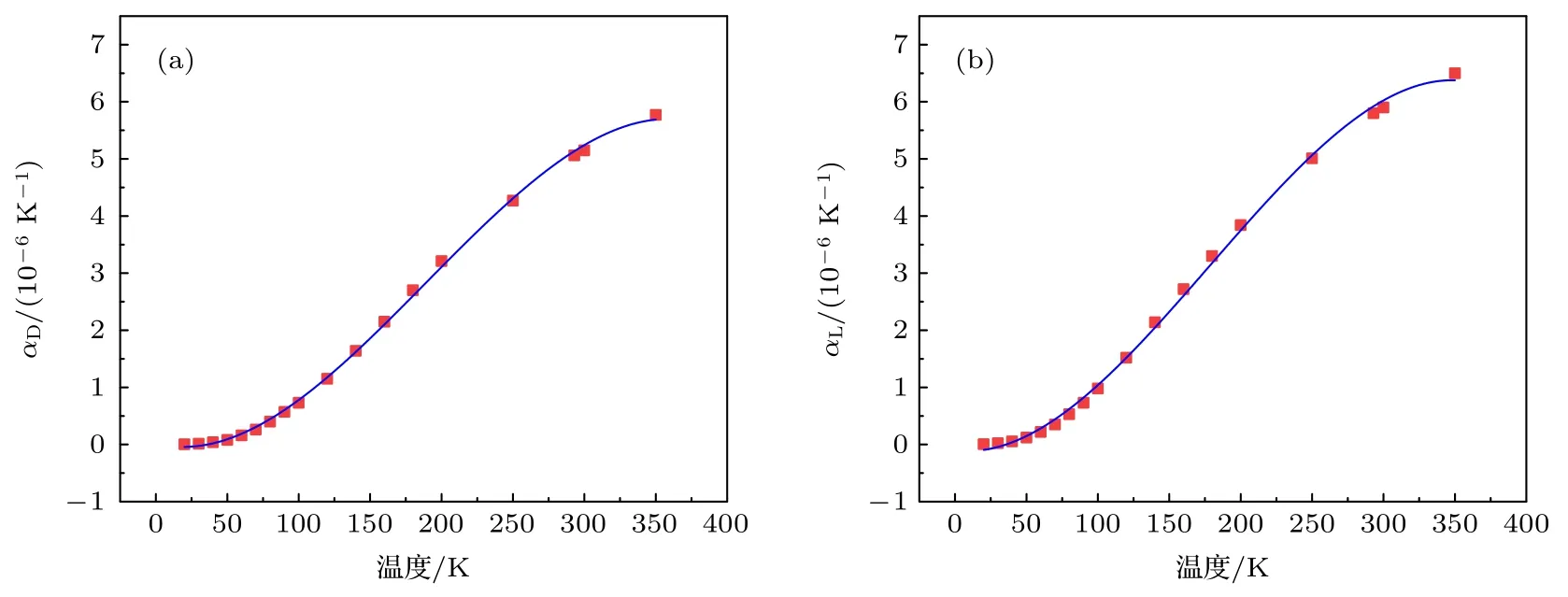
圖10 溫度對熱膨脹系數的影響 (a) αD 與溫度的關系;(b) αL 與溫度的關系Fig.10.Influence of temperature and thermal coefficient of expansion: (a) Relationship between αD and temperature;(b) relationship between αL and temperature.

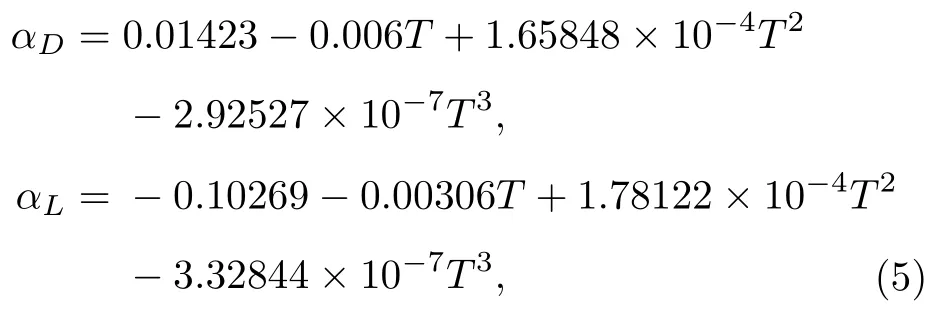
當溫度是292 K 時,根據(5)式可得,αD=5.12×10-6,αL=5.90×10-6.比較可知,介電常數溫度系數對溫度的敏感度比熱膨脹系數約大10 倍,因此,藍寶石諧振體工作在WGH 回音壁模式時,頻率-溫度敏感度主要與平行于晶軸方向的介電常數溫度系數有關.根據(4)式可得,當溫度為292 K時,藍寶石諧振體工作在WGH 回音壁模式的頻率-溫度敏感度約為 71.64×10-6.因此,為了使藍寶石諧振體有較高的中短期頻率穩定度,需要采用精密的溫控技術或者對頻率-溫度敏感度進行補償.

4 結論

本文以藍寶石諧振體為基礎,通過理論分析和模擬仿真,對藍寶石諧振體工作在WGH15,0,0模式下的尺寸、結構進行了優化設計.理論計算了藍寶石諧振體高度和直徑以及相對介電常數對諧振頻率的影響.通過對藍寶石諧振體進行耦合測試與調節,最終實現了藍寶石諧振體的諧振頻率為9.891 GHz,無載Q值為94000,由此可制成具有低相位噪聲特性的微波振蕩器.