對數(shù)均值不等式及其應用
2022-12-10 03:28:44黃瀚元
數(shù)理化解題研究 2022年31期
關(guān)鍵詞:解題
黃瀚元
(廣西壯族自治區(qū)柳州高級中學 545006)

在近些年的高考與模擬考試卷中,以上述不等式為背景的試題屢見不鮮,如果我們能掌握并熟練運用上述不等式,那么我們的解題思路就可以清晰自然,解題過程就可以簡潔通暢,為此,我們有必要對此不等式做深入研究.
1 對數(shù)均值不等式的證明

下面我們來證明這個不等式.
不失一般性,不妨設(shè)a>b.



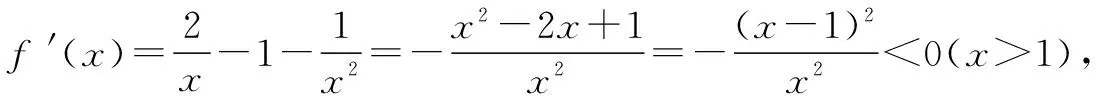
所以函數(shù)f(x)在區(qū)間(1,+∞)單調(diào)遞減.
故f(x) 所以函數(shù)g(x)在區(qū)間(1,+∞)單調(diào)遞增. 故g(x)>g(1)=0. 證畢. 結(jié)合上述證明過程,我們可以得到兩個重要的不等式鏈: 用圖象表示如圖1、圖2所示: 圖1 圖2 如果我們把對數(shù)均值不等式中的a,b分別用ea,eb替換,則可得到: 我們把它叫做指數(shù)均值不等式. 證明由對數(shù)基本不等式可知 把上式中的a,b分別用x+1,x替換,得 證明由對數(shù)基本不等式可知 把上式中的a,b分別用n+1,n替換,得 證明由對數(shù)基本不等式可知 例4 方程lnx=ax有兩個不相等的實數(shù)解x1,x2,證明:x1+x2>2e. 由對數(shù)均值不等式可得 所以lnx1+lnx2>2?x1x2>e2. 例5 已知函數(shù)f(x)=x-aex有兩個不同的零點x1,x2,求證:x1+x2>2. 又因為x1,x2是f(x)的兩個極值點, 所以x1>0,x2>0,且x1+x2=a,x1x2=1. 又由對數(shù)均值不等式可知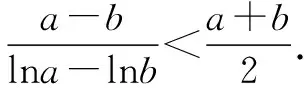


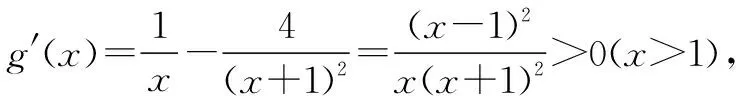

2 對數(shù)均值不等式的推論



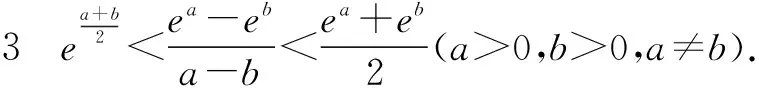
3 對數(shù)均值不等式的應用


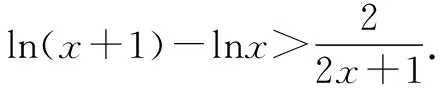







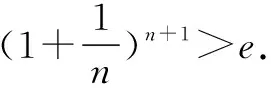



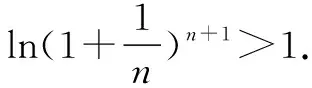
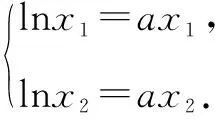

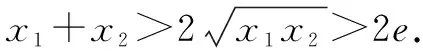
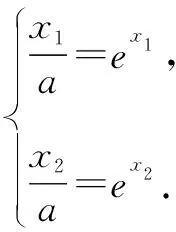
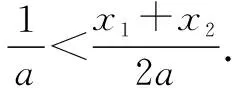
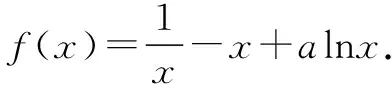




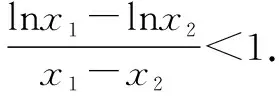


猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數(shù)理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中學數(shù)學雜志(2019年1期)2019-04-03 00:35:46
中學生數(shù)理化·中考版(2018年11期)2019-01-31 06:18:02
數(shù)學小靈通·3-4年級(2017年12期)2018-01-23 03:37:54
數(shù)理化解題研究(2017年4期)2017-05-04 04:07:56
讀寫算(下)(2016年11期)2016-05-04 03:44:22
中學生數(shù)理化·八年級數(shù)學人教版(2016年3期)2016-04-13 09:17:06
中學生數(shù)理化(高中版.高二數(shù)學)(2016年10期)2016-03-01 03:46:37

