不可忽視的定義域

李文東

(廣東省中山市中山紀念中學 528454)

函數的定義域是函數三大要素之一，而數列是特殊的函數，因此在解決與函數或數列問題時我們需要時刻關注定義域，如果忽略它，常常會使解題出現各種不必要的錯誤，出現“失之毫厘謬以千里”情況．本文針對幾種常見忽略定義域的典型問題進行歸納和總結.

1 求解函數的單調性、奇偶性和周期性問題忽略定義域

判斷函數的奇偶性不考慮函數的定義域是否關于原點對稱而導致錯誤.

例1 判斷函數的奇偶性.

正解實際上，此函數的定義域為[-1,1)，正確答案為：非奇非偶函數.

(2)錯解顯然f(x)滿足f(-x)=f(x)，故函數f(x)為偶函數.

正解函數f(x)的定義域為{-1,1}，且f(1)=f(-1)=0，故函數f(x)既是奇函數又是偶函數.

例2 求函數f(x)=x2-2lnx的單調區間.

正解由于f(x)的定義域為(0,+∞)，故f(x)的遞增區間為(1,+∞)，單調遞減區間為(0,1).

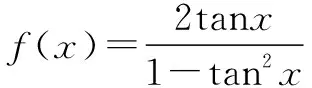
2 求解函數值域或最值問題忽略定義域

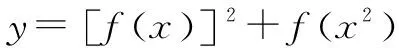
A.33 B.22 C.13 D.6

錯解y=(2+log3x)2+2+log3x2=(log3x)2+6log3x+6=(log3x+3)2-3．

因為1≤x≤9，所以0≤log3x≤2.

所以當x=9，即log3x=2時，ymax=22．

正解因為f(x)的定義域為[1,9]，

因為y=(2+log3x)2+2+log3x2=(log3x)2+6log3x+6=(log3x+3)2-3，

所以當x=3，即log3x=1時，ymax=13．

3 函數作圖時忽略定義域

解析方程f(x)=0解的個數

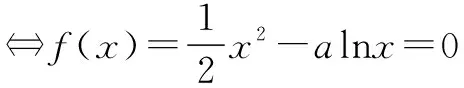
作出f(x)的圖象如圖1所示，由此可知：當a∈[0,e)時，方程無解；當a<0或a=e時，方程有唯一解； 當a>e時方程有兩解.

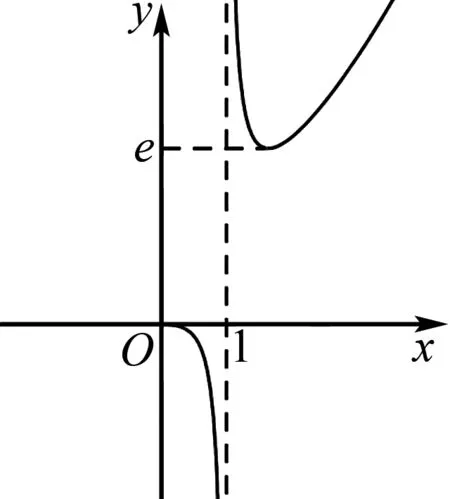
圖1

4 求解數列的單調性問題忽略定義域

數列是定義域為N*或{1,2,…,n}的函數，因此我們可以利用函數的思想來研究數列{an}問題，比如單調性，但是要注意到數列的定義域！

例6 已知數列{an}中，an=n2+λn，且{an}是遞增數列，求實數λ的取值范圍.

5 求解數列的通項問題忽略定義域

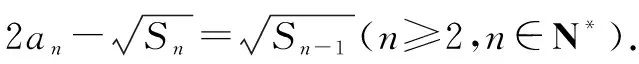
(1)求數列{an}的通項公式;

當n=1時,a1=1,

①

②

即bn=2(2n+1).

當n=1時，T1=b1=9，

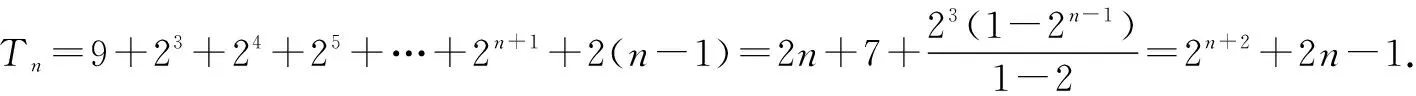
當n=1時，T1=9也滿足上式，

綜上，Tn=2n+2+2n-1.

③

④

當n=1時，T1=b1=9,

當n=2時，T2=b1+b2=14,

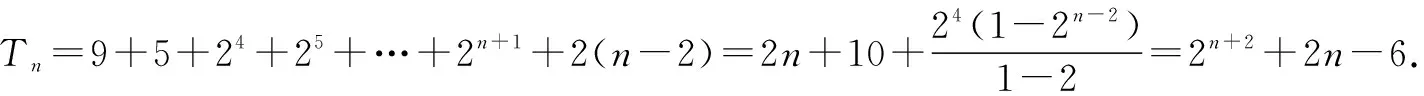
當n=2時，T2=14也滿足上式，