一類高考試題隱藏的一個秘密

傅建民

(陜西省咸陽市渭城中學 712000)

首先介紹射影幾何當中的幾個結論：

定理1設點P關于常態二次曲線Φ的極線為l，過點P的直線l′與常態二次曲線Φ交于M，N兩點，若直線l′與極線l交于點Q(如圖1)，則點列M,N,P,Q為調和點列.

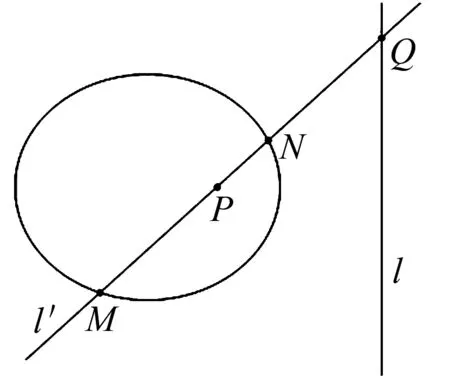
圖1

定理2如果線束S的四直線a,b,c,d被一條直線s所截，交點順次為A,B,C,D(如圖2)，則它們的交比相等，即(AB,CD)=(ab,cd).

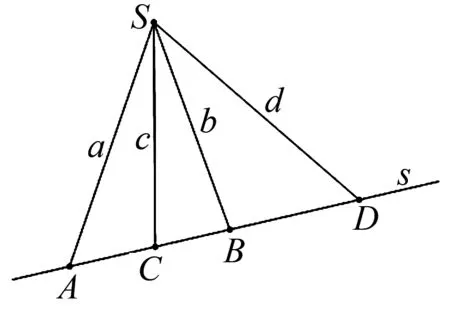
圖2

因此調和點列對應的線束為調和線束.

定理3如果調和線束S的四直線a,b,c,d被一條平行于直線d的直線s所截，交點順次為A,B,C(如圖3)，則C為線段AB的中點.

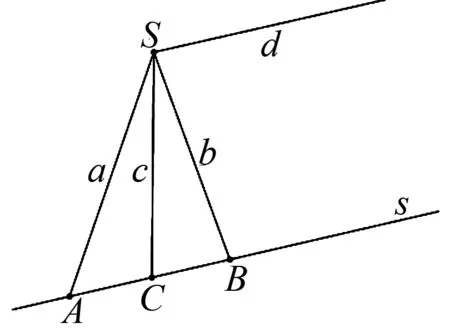
圖3

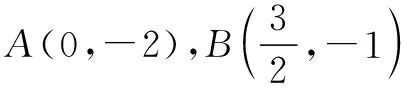
(1)求E的方程；

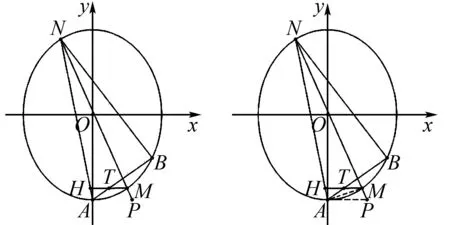
圖4 圖5

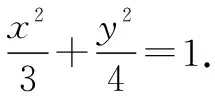
連接AP,AM，如圖5，由定理1，2可知，線束AM,AN,AB,AP為調和線束.

又因為MH∥AP，由定理3可知，T為HM的中點，即直線HN過定點A.

下面我們從解析幾何的角度來分析.

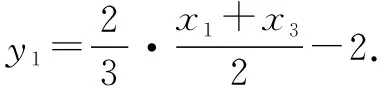
所以3y1=x1+x3-6.

所以x3=3y1-x1+6.

如果直線MN∥y軸，

因為點T在直線AB上，

可以驗證N,H,A三點共線.

如果直線MN的斜率存在，設直線MN方程為y+2=k(x-1),所以y=kx-(k+2).

整理,得

(4+3k2)x2-6k(k+2)x+3k(k+4)=0.

其中Δ=[6k(k+2)]2-4(4+3k2)[3k(k+4)]>0,

解得k>2或k<0.

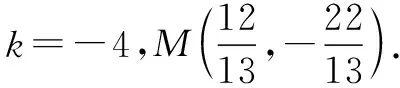
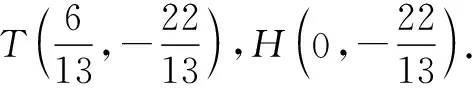
此時，N,H,A三點共線于y軸.

如果x2≠0，那么x3≠0.

下面驗證直線HN過定點A:

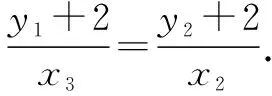
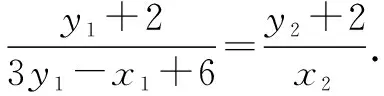
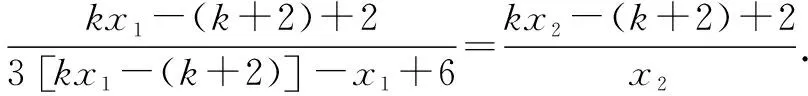
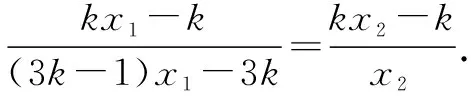
即(3k-1)kx1x2-k(3k-1)x1-3k2x2+3k2=kx1x2-kx2.

即(3k-2)kx1x2-k(3k-1)(x1+x2)+3k2=0.

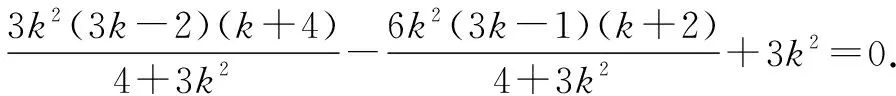
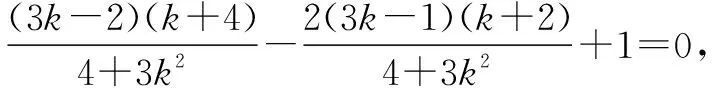
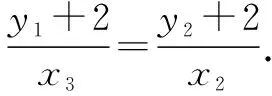
即直線HN過定點A.

(1)求橢圓E的方程；

(2)如圖6，過點P(-2, 1)作斜率為k的直線與橢圓E交于不同的兩點B,C，直線AB,AC分別與x軸交于點M,N，當|MN|=2時，求k的值.

圖6 圖7

(2)記橢圓E的左頂點為D，如圖7，連接AP,AD，點P與直線AD恰好是一對極點極線，因此線束AC,AB,AD,AP為調和線束.

又因為AP平行x軸，所以點D為線段MN的中點.下面我們用解析法來求解該問題(2)

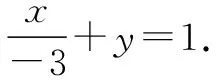
即x=3y-3.

即13y2-18y+5=0.

即(13y-5)(y-1)=0.

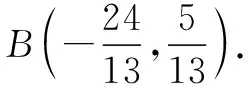
所以直線PB的斜率

即x=y-1.

代入橢圓方程,得

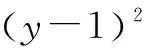
即5y2-2y-3=0.

即(5y+3)(y-1)=0.

所以直線PC的斜率

所以P,B，C三點共線.

故所求的直線的斜率k=-4.

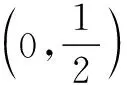
圖8 圖9

(1)求拋物線C的方程，并求其焦點坐標和準線方程；

(2)求證：A為線段BM的中點.

解析(1)因為拋物線y2=2px經過點P(1, 1)，所以1=2p.

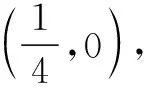
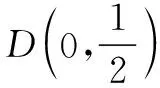
設OP與l的交點為G，則M,N,G,D為調和點列，所以OM,ON,OG,OD為調和線束.即OM,OB,OA,OD為調和線束，而直線MA∥OD，所以A為線段BM的中點.

通過上面例題的解析，我們洞悉了出題人的構題思路.對于解題者來說，通過射影幾何發現了問題當中的玄機，從而將探索性問題變成了驗證性問題，大大減少了計算量.