解析幾何中的最值問題

廖永福

(福建省廈門第二中學 361009)

解析幾何中的最值問題涉及的知識面較廣，綜合性較強，因而常以中檔題或壓軸題的形式出現.解決這類問題的常用方法有代數法、幾何法和三角法等.

1 代數法

代數法就是將題目中某些變化的幾何量(如斜率、坐標等)設為自變量，并用它表示目標變量(如弦長、距離、周長、面積等)，即建立目標函數，然后應用函數或不等式等知識解決問題的一種方法.應用代數法重在運算，要做到運算準確，還要注意函數的定義域，否則容易出錯.

例1(2021年北京卷9)已知圓C:x2+y2=4，直線l:y=kx+m，若當k的值發生變化時，直線被圓C所截的弦長的最小值為2，則m的取值為( ).

分析先求得圓心到直線的距離，即可表示出弦長，再根據弦長的最小值求出m.

解析由已知得圓心為(0,0)，半徑為2.

當k=0時，弦長取最小值2，即

故選C.

點評本題主要考查直線與圓的位置關系，點到直線的距離公式和簡單函數的性質等，體現了直觀想象、邏輯推理和數學運算等核心素養，解題關鍵是利用勾股定理將弦長表示成斜率的函數，再利用函數的性質求解，屬于基礎題.

例2(2017年全國Ⅰ卷理10)已知F為拋物線C：y2=4x的焦點，過點F作兩條互相垂直的直線l1，l2，直線l1與C交于A，B兩點，直線l2與C交于D，E兩點，則|AB|+|DE|的最小值為( ).

A．16 B．14 C．12 D．10

分析先寫出|AB|,|DE|的表達式，再利用基本不等式求出|AB|+|DE|的最小值.

故直線l1,l2的方程分別為

k2x2-(2k2+4)x+k2=0.

同理可得|DE|=4k2+4.

點評本題主要考查直線與拋物線的位置關系，弦長公式和基本不等式等，體現了直觀想象、邏輯推理和數學運算等核心素養，解題關鍵是將|AB|+|DE|表示成直線l1的斜率的函數，再用基本不等式求解，屬于中檔題.

2 幾何法

幾何法就是充分挖掘題目中隱含的幾何意義與幾何特征，應用圓錐曲線的定義或平面幾何的知識解決問題的一種方法.應用幾何法重在推理，要做到思維嚴謹，步步有據.

分析根據雙曲線的定義等價轉化|PF|，分析何時△APF的周長最小，然后用間接法計算S△APF.

故F(3,0),F′(-3,0).

當點P在雙曲線左支上運動時，由雙曲線定義知|PF|-|PF′|=2.

所以|PF|=|PF′|+2.

從而△APF的周長=|PA|+|PF|+|AF|=|PA|+|PF′|+2+|AF|.

圖1

點評本題主要考查雙曲線的標準方程及其幾何性質，考查三角形的周長和面積等，體現了直觀想象、邏輯推理和數學運算等核心素養，解題關鍵是根據雙曲線的定義等價轉化|PF|，找到△APF的周長取最小值時點P的位置，屬于中檔題.

化簡,得2x2-mx+4=0.

點評本題主要考查直線與曲線的位置關系，點到直線的距離和平行線間的距離等，體現了直觀想象、邏輯推理和數學運算等核心素養，解題關鍵是將動點到定直線的距離問題轉化為兩條平行直線間的距離，屬于中檔題.

變式練習2(2020年全國Ⅰ卷理11)已知⊙M：x2+y2-2x-2y-2=0，直線l：2x+y+2=0，P為l上的動點，過點P作⊙M的切線PA,PB，切點為A,B，當|PM|·|AB|最小時，直線AB的方程為( ).

A．2x-y-1=0 B．2x+y-1=0

C．2x-y+1=0 D．2x+y+1=0

3 三角法

例5(2018年北京卷理7)在平面直角坐標系中，記d為點P(cosθ,sinθ)到直線x-my-2=0的距離，當θ，m變化時，d的最大值為( ).

A．1 B．2 C．3 D．4

分析根據點到直線的距離公式，將d表示成θ和m的函數，再分別把θ和m看作自變量，利用函數的性質求解.

解析由點到直線的距離公式，得

點評本題主要考查點到直線的距離公式，二次函數和三角函數的性質等，體現了邏輯推理和數學運算等核心素養，解題關鍵是將d表示成θ和m的函數，再利用函數的性質求解，屬于中檔題.

例6 (2021年全國乙卷理21)已知拋物線C:x2=2py(p>0)的焦點為F，且F與圓M:x2+(y+4)2=1上點的距離的最小值為4．

(1)求p；

(2)若點P在M上，PA,PB是C的兩條切線，A,B是切點，求△PAB面積的最大值．

解得p=2.

(2)拋物線C的方程為x2=4y.

因為點P在M上，可設P(cosθ,-4+sinθ)，θ∈[0，2π).

由已知，過點P的拋物線C的切線l斜率存在，記作k，則l的方程為

y=k(x-cosθ)-4+sinθ.

x2-4kx+4kcosθ-4sinθ+16=0.

因為l與C相切，所以

△=16k2-4(4kcosθ-4sinθ+16)=0.

即k2-kcosθ+sinθ-4=0,

(*)

且切點為(2k,k2).

設切線PA,PB的斜率分別為k1,k2，則

直線AB的斜率

直線AB的方程為

因為k1,k2是方程(*)的兩個根，

所以k1+k2=cosθ,k1k2=-4+sinθ.

所以P(k1+k2,k1k2).

因為點P到直線AB的距離

所以△PAB面積

點評本題主要考查圓與拋物線的標準方程和幾何性質，直線與拋物線的位置關系以及三角形的面積公式等，體現了直觀想象、邏輯推理和數學運算等核心素養，解題關鍵是引進參數θ，將△PAB的面積表示成θ的函數，屬于難題.

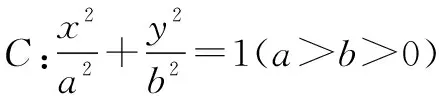
(1)求C的方程；

(2)點N為橢圓上任意一點，求△AMN的面積的最大值.

變式練習答案：