強化“幾何”特征 重視“結合”意識
——例談解析幾何中強化“幾何”特征和綜合解題意識培養

巨小鵬

(陜西省漢中市龍崗學校 723102)

解析幾何問題首先要搞明白試題要解決的是什么樣的幾何問題，其次要弄清楚解決這個幾何問題是否需要轉化至代數問題解決，如果需要，是否需要建立坐標系，如果可以借助幾何特征解題，那么借助哪些幾何特征或幾何工具，或者看是否需要數形結合，代數和幾何相互借力，將復雜問題等價轉化至較為簡單的問題(有時候這個轉化過程不是很直觀，需要把幾何問題轉化為另一個等價的幾何問題后再進行代數化)，利用已知的題設條件，分析這些條件之間的聯系，研究并解決轉化之后的問題，從而解決解析幾何問題.

1 利用“幾何”特征，培養直觀想象能力

例1(2019年全國Ⅰ卷·10)如圖1，已知橢圓C的焦點為F1(-1,0)，F2(1,0)，過點F2的直線與C交于A，B兩點.若|AF2|=2|F2B|，|AB|=|BF1|，則C的方程為( ).

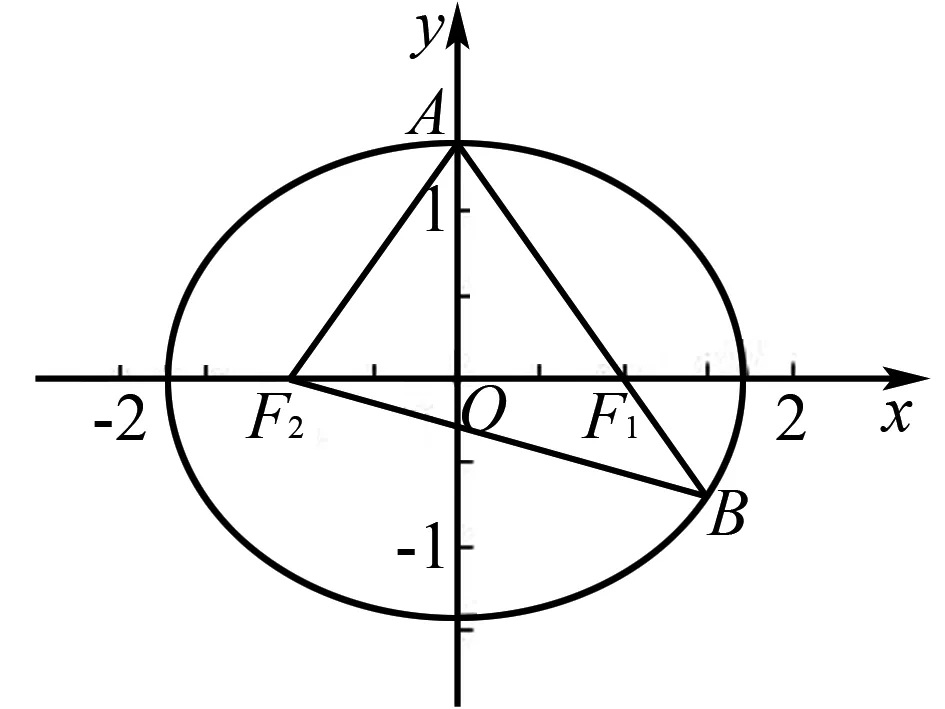
圖1

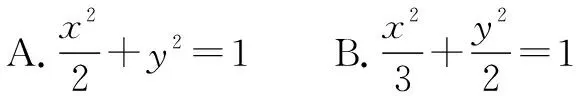
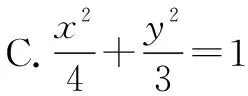
解法1(同角視角法) 由已知設|F2B|=m，則|AF2|=2m,|BF1|=|AB|=3m.

根據橢圓的定義知|BF1|+|BF2|=4m.

則|AF1|=2a-|AF2|=2m.

在△AF1B中，由余弦定理得

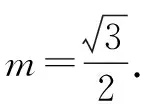
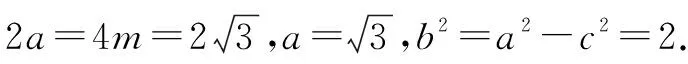
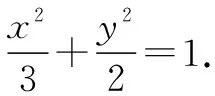
解法2(鄰補角法)由解法1可知

|BF1|=|AB|=3m，|AF1|=2m.

則在△AF1F2和△BF1F2中，由余弦定理,得

又由圖可知∠AF2F1+∠BF2F1=π.

則cos∠AF2F1+cos∠BF2F1=0.

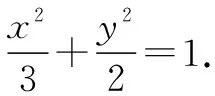
代入橢圓方程得a2=3,b2=a2-c2=2.

故選B.

評注本題考查橢圓定義及其簡單性質，考查數形結合思想、轉化與化歸的能力，特別是利用幾何特征解題，形象直觀，解法1把一個角放在不同的三角形中研究，利用余弦定理建立方程解決問題，解法2利用鄰補角的余弦值互為相反數解決問題，解法3借助輔助線利用已知線段比建立相似比解決問題，很好地考查了直觀想象能力和邏輯推理能力.

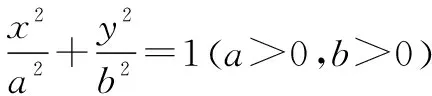
根據橢圓定義可知

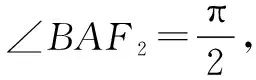
即(3m)2+(2a-2m)2=(2a-m)2，

解得a=3m.

在△AF1F2中，直線AB的斜率為

因為a=3m，在Rt△AF1F2中，

評注利用平面幾何解題更加直觀，本題利用圖形的“幾何”特征，在幾何圖形中尋找等量關系，結合橢圓定義和解三角形計算，從而求出直線的斜率和橢圓的離心率，考查推理分析、運算和圖形分析能力.

2 代數幾何相結合，彼此借力內化思維品質

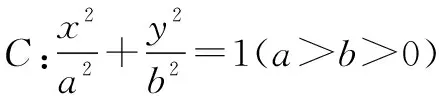
圖2

(1)求橢圓C的標準方程；

(2)求點E的坐標.

解析(1)可知F1(-1，0)，F2(1，0)，所以F1F2=2，c=1.

因此2a=DF1+DF2=4.

從而a=2.解得b2=3.

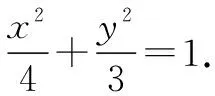
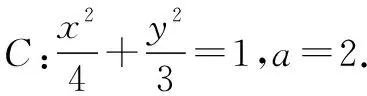
因為AF2⊥x軸，將x=1代入圓F2的方程(x-1)2+y2=16，得y=±4.

因為點A在x軸上方，所以A(1，4).

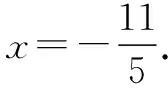
又因為E是線段BF2與橢圓的交點，

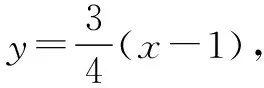
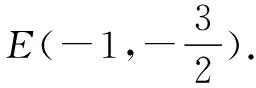
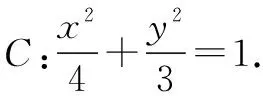
圖3

從而∠BF1E=∠B.

因為F2A=F2B，所以∠A=∠B.

所以∠A=∠BF1E.

從而EF1∥F2A.

因為AF2⊥x軸，所以EF1⊥x軸.

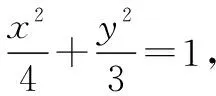
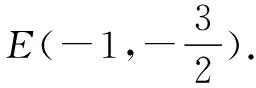
評注解法1明顯比解法2計算復雜，利用平面幾何知識，從“幾何”特征入手研究題目中的幾何關系是必要的，在這個過程中，要經歷文字信息、圖像特點和符號語言之間的多重轉換.

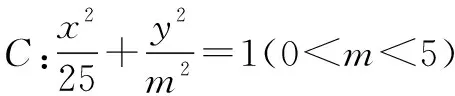
(1)求C的方程；

(2)若點P在C上，點Q在直線x=6上，且|BP|=|BQ|，BP⊥BQ，求△APQ的面積.

(2)解法1 (通性通法)設P,Q在x軸上方，過點P作x軸垂線，垂足為點M，設直線x=6與x軸交點為N，根據題意畫出圖形，如圖4.

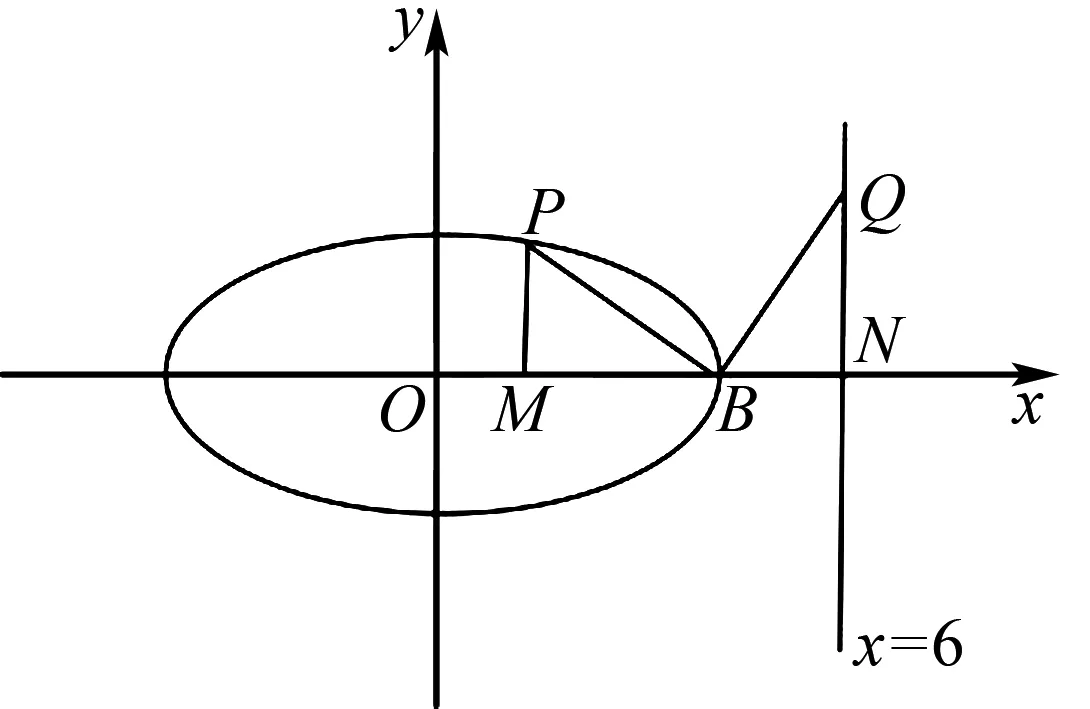
圖4

因為|BP|=|BQ|，BP⊥BQ， ∠PMB=∠QNB=90°，∠PBM+∠QBN=90°， ∠BQN+∠QBN=90°，所以∠PBM=∠BQN.

根據三角形全等可得△PMB≌△BNQ.

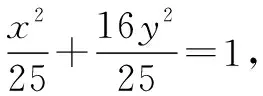
所以|PM|=|BN|=6-5=1.

設點P為(xP,yP)，可得點P縱坐標為yP=1.

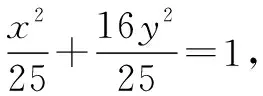
解得xP=3或xP=-3.

所以點P為(3,1)或(-3,1).

①當點P為(3,1)時，|MB|=5-3=2.

因為△PMB≌△BNQ，

所以|MB|=|NQ|=2.

可得點Q為(6,2).

如圖5,因為A(-5,0),Q(6,2)，可求得直線AQ的直線方程為2x-11y+10=0.

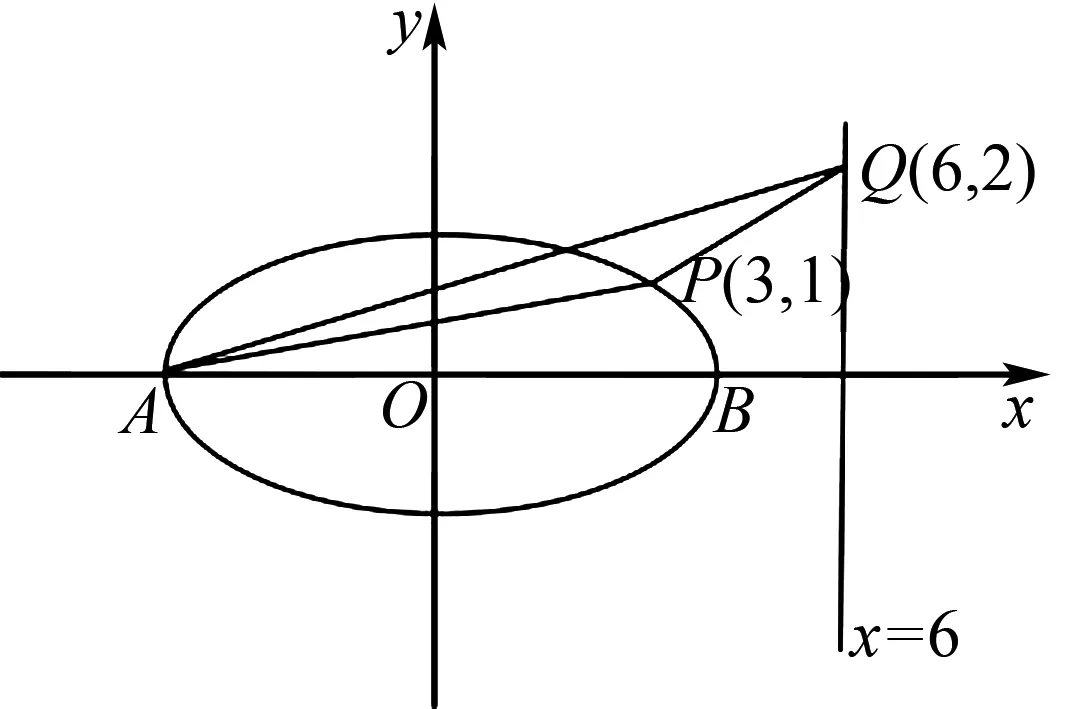
圖5

可得P到直線AQ的距離為

②當點P為(-3,1)時，|MB|=5+3=8.

因為△PMB≌△BNQ，所以|MB|=|NQ|=8.

所以點Q為(6,8)

如圖6，,因為A(-5,0),Q(6,8)，直線AQ的方程為8x-11y+40=0，可得點P到直線AQ的距離為

圖6

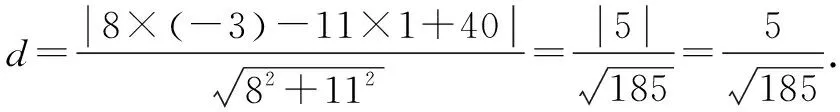
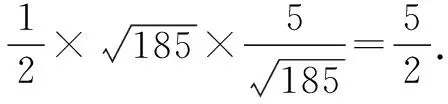
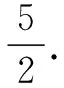
解法2(分割面積法)由對稱性，不妨設點P，Q在x軸上方，過點P作PE⊥x軸，垂足為點E.設D(6,0)，由題知，△PEB≌△BDQ.

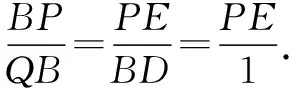
所以PE=1.所以xp=±3.

圖7

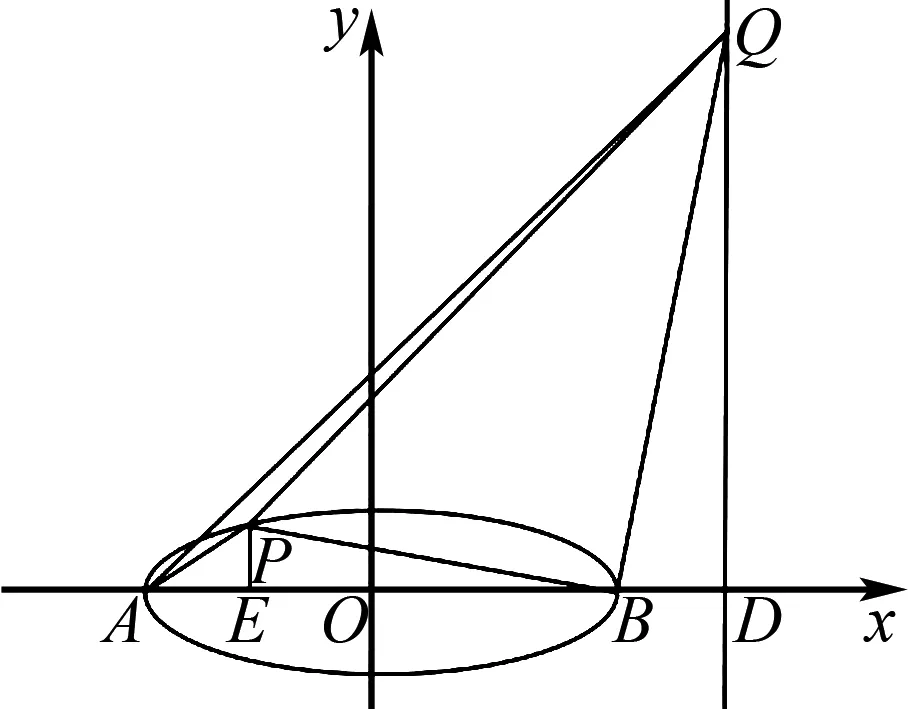
圖8

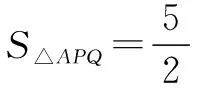
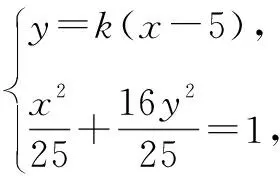
(1+16k2)x2-160k2x+16×25k2-25=0.

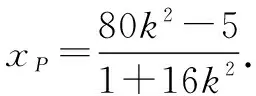
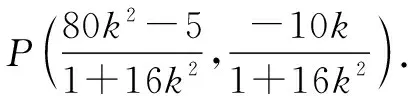
因為BP⊥BQ，則直線BQ的方程為

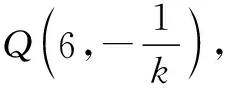
因為|BP|=|BQ|，

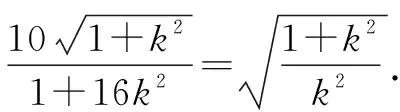
即256k4-68k2+1=0.

即(64k2-1)(4k2-1)=0.

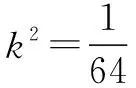
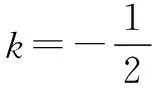
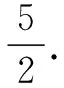
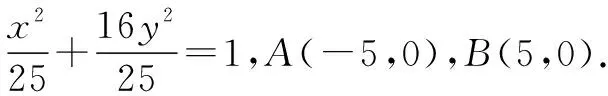
不妨設P(x0,y0)在x軸上方.

設直線AP:y=k(x+5)(k>0),

因為|BP|=|BQ|,BP⊥BQ，

所以y0=|BN|=1,yQ=|BM|=5-x0.

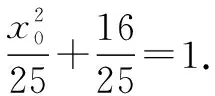
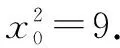
由點P在直線AP上得1=k(x0+5).

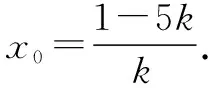
化簡得16k2=10k-1.

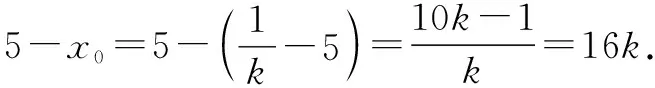
即Q(6,16k).

所以點Q到直線AP的距離

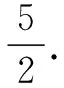
解法5(面積坐標法) 由對稱性，不妨設點P，Q在x軸上方，過點P作PC⊥x軸，垂足為點C，設D(6,0)，由題知△PCB≌△BDQ.

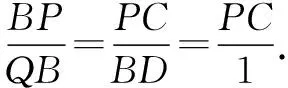
所以PC=1.

所以xp=±3.

當P(3,1),A(-5,0),Q(6,2),則

當P(-3,1),A(-5,0),Q(6,8),同理，

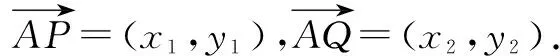
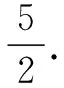
評注對于第(2)問解決視角很多，解法1根據平面幾何知識，利用“幾何”特征可求得點P的坐標，從而得到點Q的坐標以及直線AQ的方程，再根據距離公式即可求出三角形的面積，也是大多數人能想到的方法，是為通性通法；解法2同解法1，最后利用圖形面積分割法求△APQ的面積，優化處理后計算有所簡化；解法2利用代數法通過設直線BP的方程y=k(x-5)與橢圓的方程聯立，求出點P的坐標，再利用等量關系求出k的值，從而得出點Q的坐標以及直線AQ的方程，最后根據距離公式即可求出三角形的面積，方法容易想到但計算量比較大；解法4與解法3類似，設直線AP的方程y=k(x+5)(k>0)，通過平面知識求出點P的坐標，表示出點Q，再根據距離公式即可求出三角形的面積，計算量也不小；解法5同解法1最后利用了三角形面積坐標法，需要很強的邏輯推理能力利用向量法推出公式，當然北師大版必修五第二章第一節正弦定理例3介紹過公式的推導過程，所以注重課本例題和習題顯得尤為重要.

解析幾何問題中幾何是思考的起點和終點，也是問題的緣起和歸宿，代數化和“幾何”特征是解決幾何問題的工具.加深幾何特征和曲線與方程有關概念的理解，以提升“猜想證明、化歸轉化、直觀想象、數學運算、嚴謹邏輯推理和探索實踐應用”等關鍵能力為目標，內化數學核心素養.