加權迭代六邊形網絡的譜分析

李 美，吳 波

（南京財經大學 應用數學學院，南京 210023）

0 引言

復雜網絡作為一門新興交叉學科，其研究涉及自然界和社會生活的很多方面，例如物理、化學、生物、社會、經濟、工程等領域.在復雜網絡的研究中，一個核心問題是掌握網絡結構，進一步了解網絡拓撲結構對網絡功能與動態性質的影響.例如，操芳等［1］通過研究網絡受到攻擊后的平均捕獲時間，對比網絡受到攻擊前后的擴散效率等.近年來，通過大量學者的研究表明網絡的拉普拉斯譜也具有重要作用.例如，Klein等［2］根據電網絡理論定義了新的函數——電阻距離，稱網絡中所有節點對之間的電阻距離之和為Kirchhoff指標，它是一個重要的拓撲指標，可以用來分析網絡中通訊的可靠性和網絡整體的魯棒性；文獻［3］將Kirchhoff指標和拉普拉斯譜聯系起來；文獻［4］進一步引出了乘法度-Kirchhoff指標，并將其和標準拉普拉斯譜聯系起來；此外，Banerjee等［5-6］總結了不同網絡的標準拉普拉斯譜的圖像，對經典網絡進行初步分類.

近年來，許多學者致力于研究網絡的譜，包括迭代三角形網絡和其他分形網絡［7-10］.一般情形下，考慮一個具有相應結構的網絡只注意節點之間是否存在連邊，忽略了節點之間連接的緊密程度，即邊的權值.因此，將一般網絡推廣到加權網絡更具有實際意義.但目前，譜的研究尚有諸多困難，除一些特殊結構的網絡模型外，譜難以解析研究.本文構造了一類加權迭代六邊形網絡，在網絡的拓撲結構的基礎上建立相鄰兩代網絡的特征值和特征向量之間的迭代關系，從而得到網絡的標準拉普拉斯譜.

1 加權迭代六邊形網絡的構成

首先我們介紹加權迭代六邊形網絡的構造，以r(0＜r＜1)為參數進行以下的迭代，得到一個加權迭代六邊形網絡，r稱為權重因子.

（i）設G為任意一個簡單連通圖，每條邊的權重為ω=1，稱G為初代圖；

（ii）用長度為1和5的兩條平行路徑代替G的每一條邊，長度為5的路徑即為新生成的路徑，5條新邊的權重為rω=r.此時，得到一個第一代的加權迭代六邊形網絡，記作W(G)；

（iii）加權迭代六邊形網絡，用Wn(G)(n≥1)表示，它是由Wn-1(G)迭代產生的.若Wn-1(G)的每一條邊ij的權重為ω，則產生4個新節點i′、j′、k′、l′和5條新邊ii′、i′j′、j′k′、k′l′、l′j，新邊的權重為rω.

圖1初始圖為三角形的加權迭代六邊形網絡，展示了該網絡前三代的迭代過程，考慮到初始圖可以是任意連通圖，所以，圖1是一個特例.將第n代加權六邊形網絡Wn(G)的總節點數記作|Nn.|設Wn是網絡Wn(G)的廣義鄰接矩陣，也稱為權重矩陣，它是一個階矩陣，每項元素wn(i,j)定義如下，如果節點i和j有連邊，則wn(i,j)是邊的權重ωn(i,j)，否則是0.設Sn為對角強度矩陣，定義為Sn=其中sn(i)表示節點i的強度，它是節點i的所有鄰邊的權重之和.于是，拉普拉斯矩陣-L n表示為-L n=Sn-Wn，而轉移概率矩陣Tn表示為Tn=Sn-1Wn.

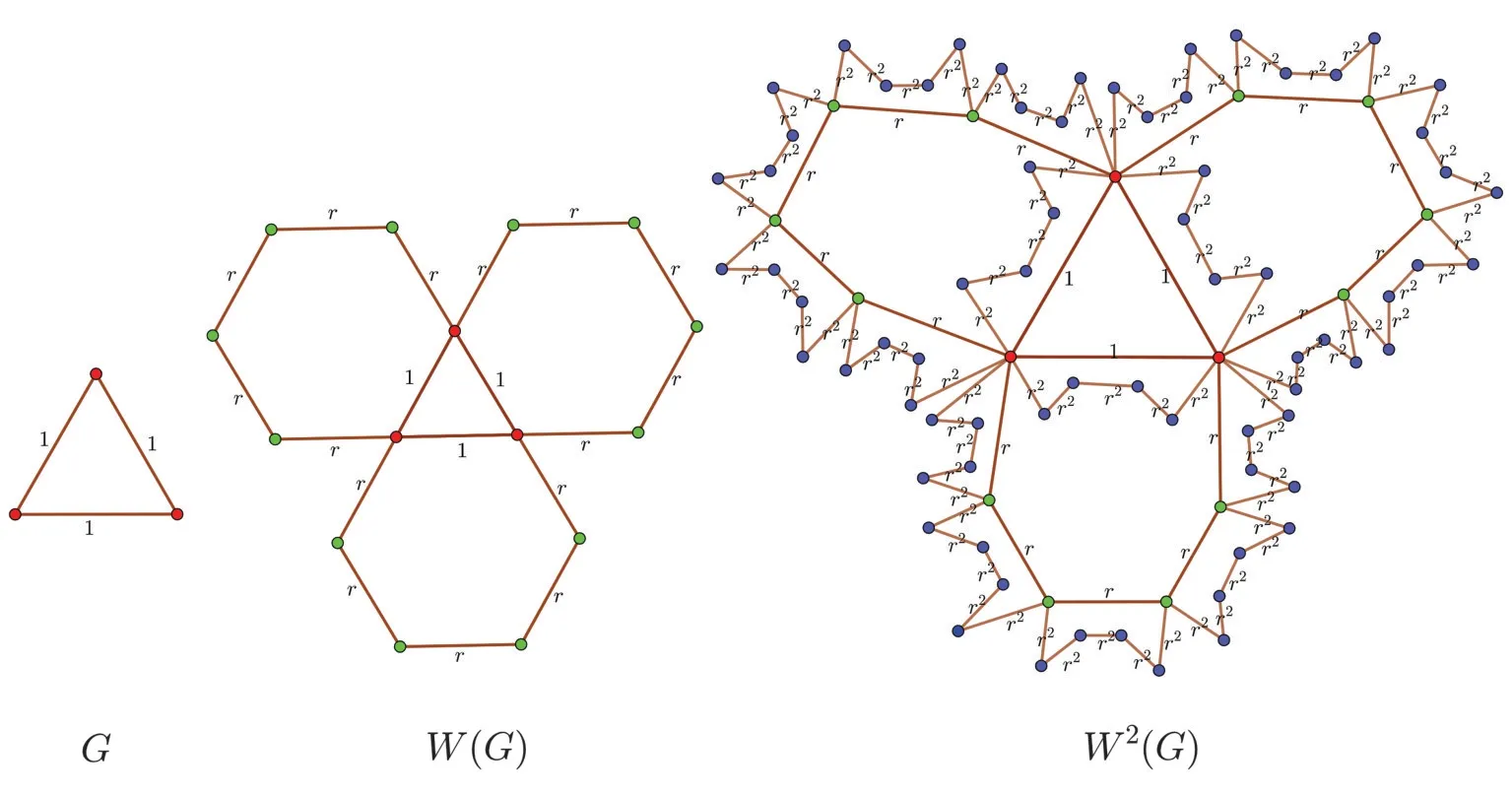
圖1 加權迭代六邊形網絡的前三代

一般情況下，轉移概率矩陣Tn是不對稱的，但是可以通過標準化將其轉化為對稱矩陣，稱為標準鄰接矩陣，記作Pn，定義為

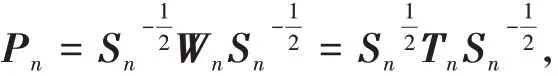
2 加權迭代六邊形網絡的譜分析

從第n(n≥1)代加權迭代六邊形網絡Wn(G)開始，根據網絡的自相似結構，得到前一代網絡Wn-1(G)的標準鄰接矩陣的特征值，利用網絡的標準鄰接矩陣和標準拉普拉斯矩陣之間的聯系，得到前一代網絡的標準拉普拉斯矩陣的特征值，即得到如下定理.

定理2.1 設λ為網絡的標準拉普拉斯矩陣Ln(n＞1)的任意一個特征值，λ≠1，r(0＜r＜1)為權重因子，滿足

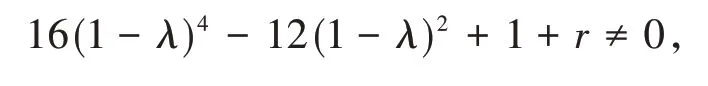
則

是Ln-1的一個特征值，且它的重數與λ的重數相等.

證明 令Vn是第n代網絡Wn(G)的所有節點集，Vn=Voldn∪Vnewn，Vnewn是第n次迭代新加入的節點集，Voldn是所有老節點集（即前一代網絡Wn-1(G)的所有節點集）.

設Vrk（k=0,1,…,n-1）是父邊權重為rk的節點集，

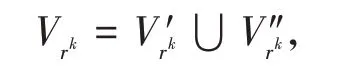
其中：Vr′k=Vrk∩Vnold；Vr″k=Vrk∩Vnnew.

易知，V0∈Vold，Vrn-1∈Vnew.于是

Vn=V0∪V1∪Vr∪…∪Vrn-1=( V0∪V1′∪Vr′∪…∪Vr′n-2)∪( V1″∪Vr″∪…∪Vr″n-2∪Vrn-1).

設v=(v1,v2,…,v|Nn|)是Ln屬于λ的特征向量，其中|Nn|為網絡Wn(G)的總節點數.

因為Ln=In-Pn，所以1-λ是標準鄰接矩陣Pn的特征值，且

于是，對任意的節點i∈Vn，有

同時，根據網絡的自相似結構，節點i的強度為

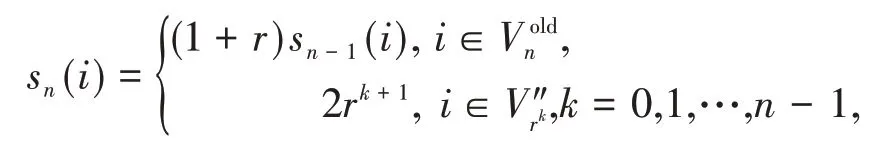
其中V″rn-1=Vrn-1.

為了得到前一代網絡的特征值，先考慮每一個老節點i∈V′rm,m=-1,0,1,…,n-2，其中當m=-1時，V′r-1=V0.相應地，有j′r-1=j0，vj′r-1=vj0.

基于網絡的自相似結構，節點i和j之間的權重為

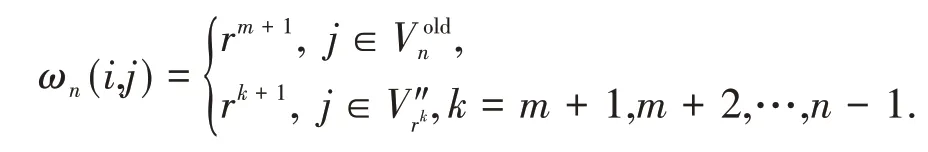
根據式（2）可得

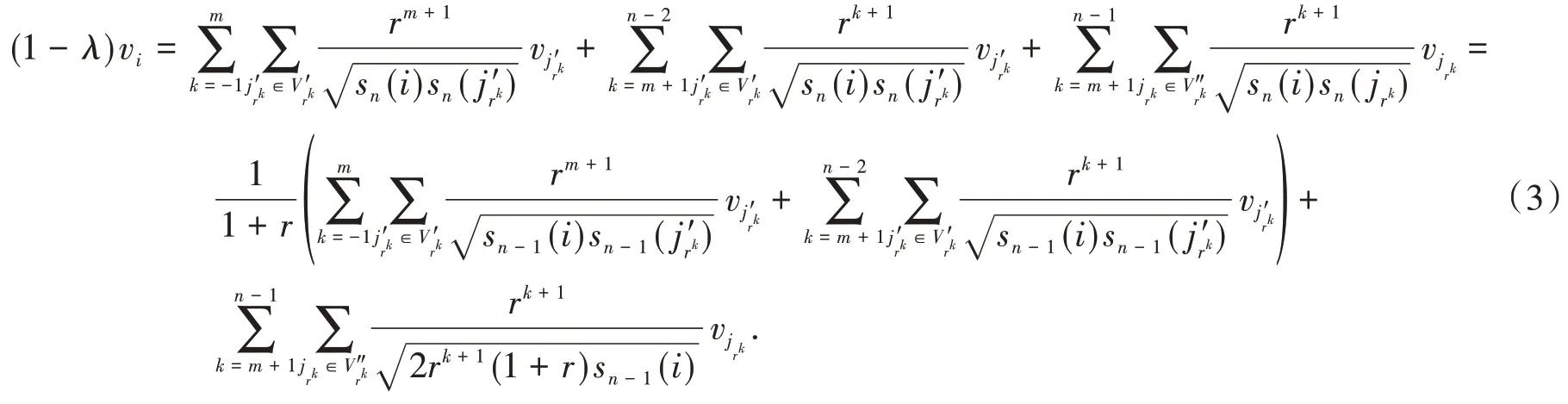
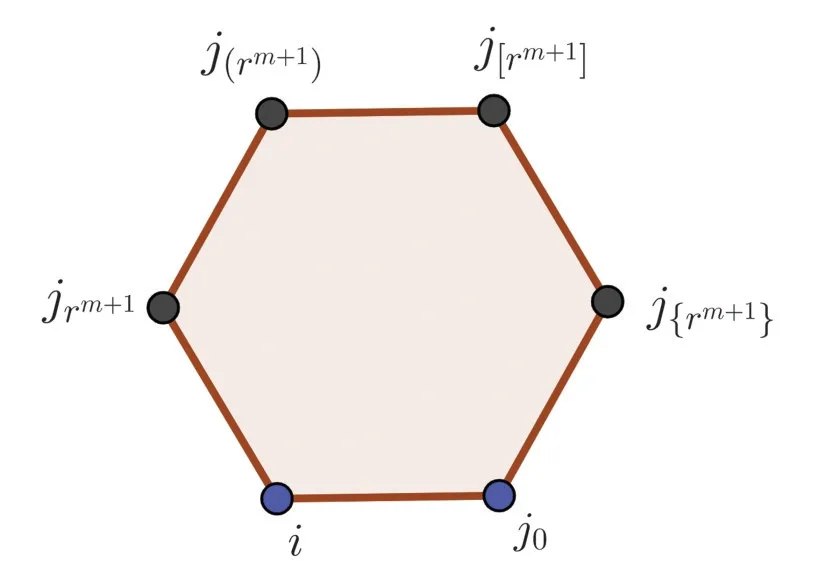
圖2 Wn(G)的部分圖

當連邊ij0是jrm+1的父邊時，有

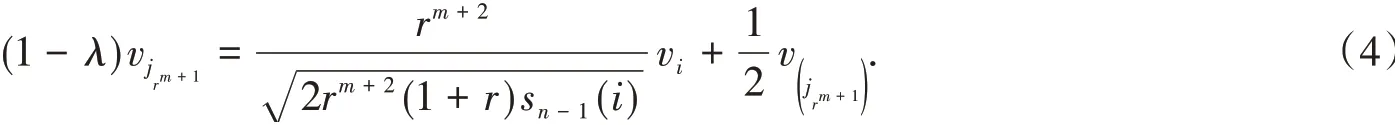
同樣地，有

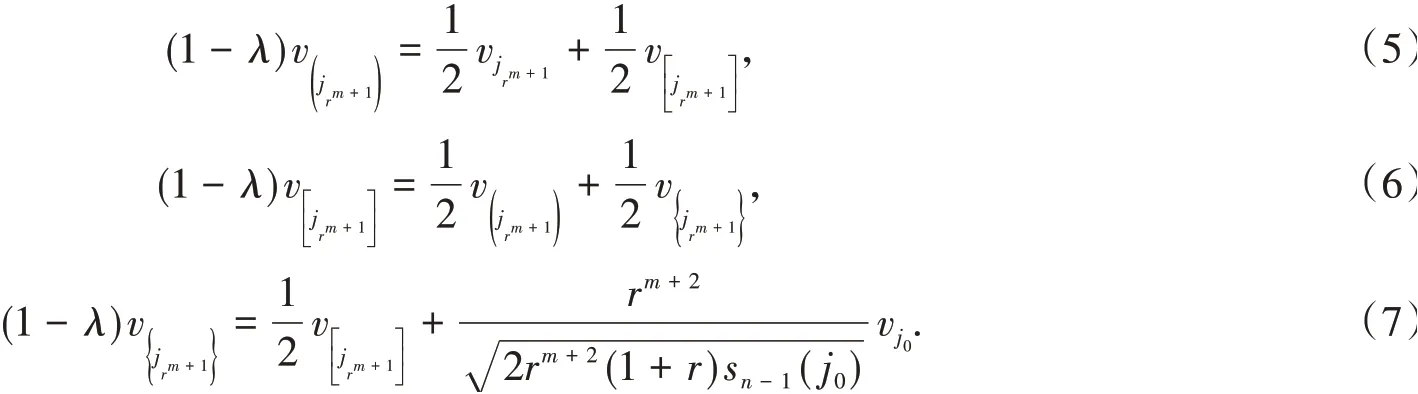
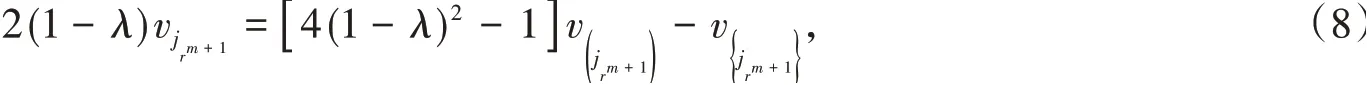
其中λ≠1.

聯立式（5）和式（7），消去v得

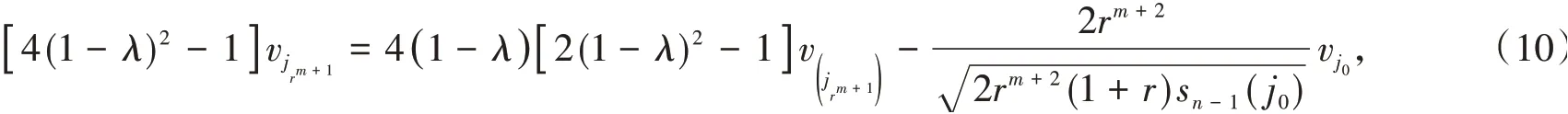
其中λ≠1.

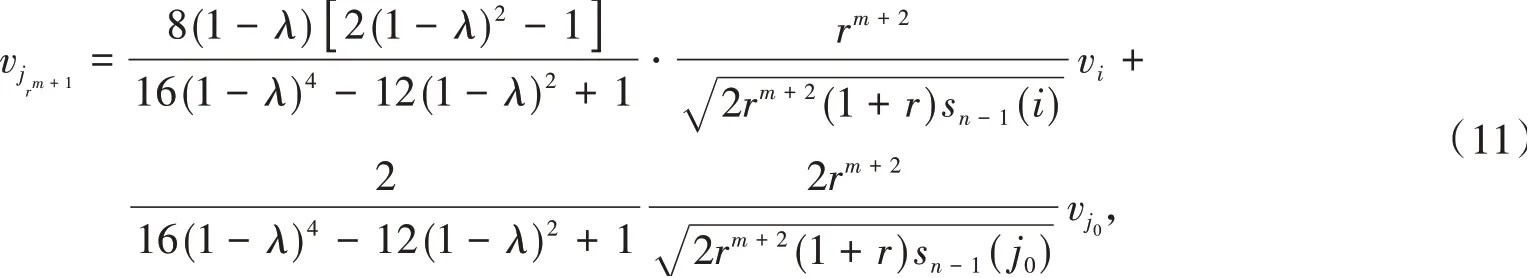
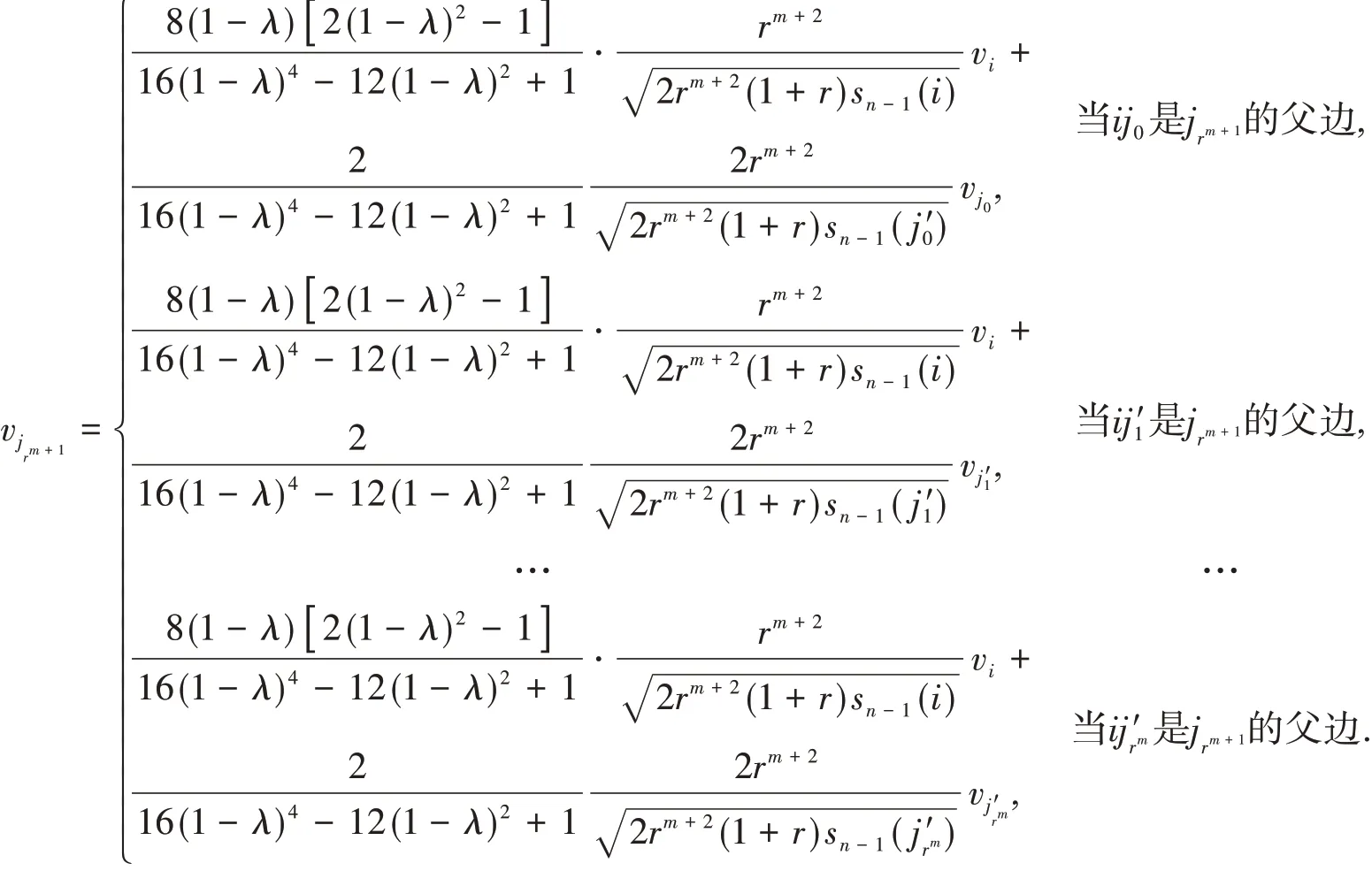
當ij′rk-1是jrk的父邊時，k=m+2,m+3,…,n-1，

將式（12）代入式（3），得

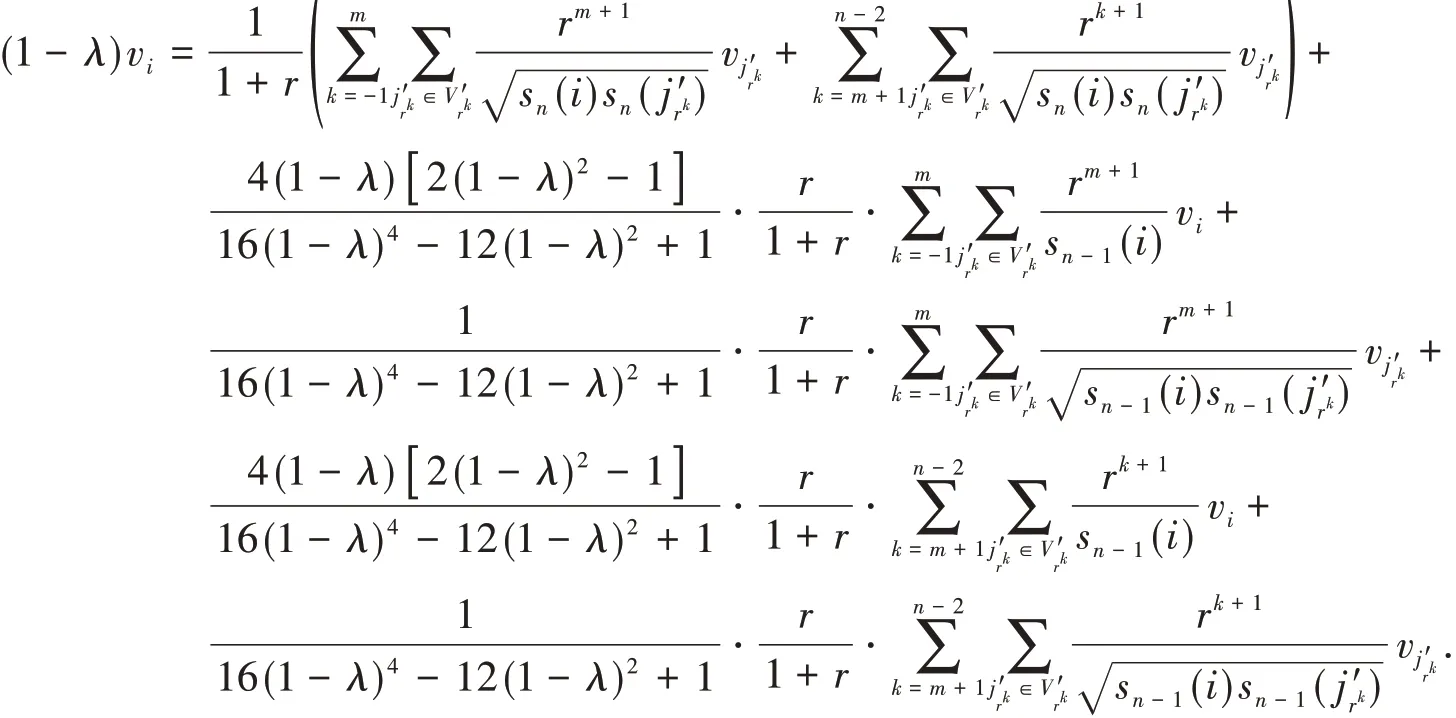
又因為

所以

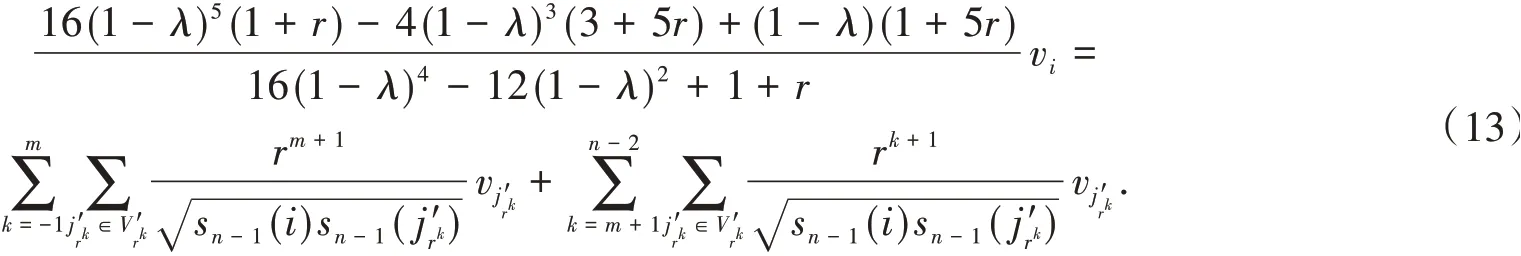
由式（13）可得前一代網絡的標準鄰接矩陣的特征值，即

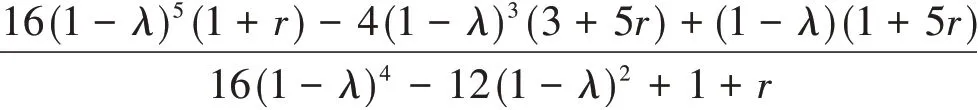
是Pn-1的特征值，記作，則

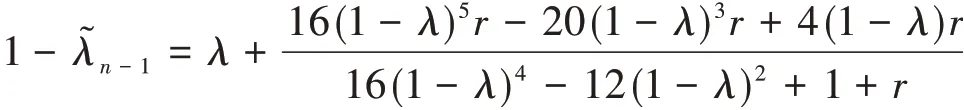
是Ln-1的特征值，記作λn-1.

最后考慮特征值的重數：易知mLn-1(λn-1)≥mLn(λ).假設mLn-1(λn-1)＞mLn(λ)，則存在Ln-1的屬于λn-1的特征向量，使其與Ln的屬于λ的特征向量無關，但是根據式（12）不存在這樣的特征向量，所以mLn-1(λn-1)=mLn(λ).證畢.

如果從第n-1代入手，依據定理2.1，反解方程，得到第n代的特征值，即定理2.2.

定理2.2 設λ為Ln-1的任意一個特征值，λ≠1，r(0＜r＜1)為權重因子.若fi(λ),i=1,2,…,5是方程

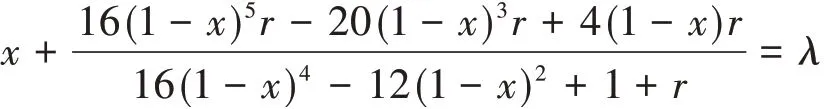
的解，則fi(λ)是Ln的特征值，且mLn(fi(λ))=mLn-1(λ),i=1,2,…,5.

證明 由定理2.1直接得到.

根據韋達定理，有

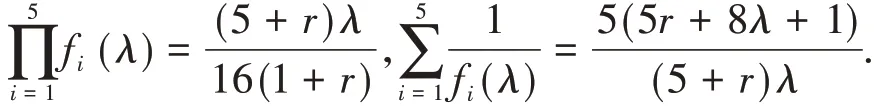
網絡的譜是所有的特征值的集合，因此，第n代網絡的譜可以通過前一代找到，得到定理2.3.

定理2.3 設網絡Wn(G)(n≥1)的標準化拉普拉斯譜是σn.

（1）當Wn(G)是二分圖時，

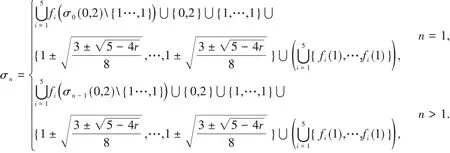
（2）當Wn(G)不是二分圖時，

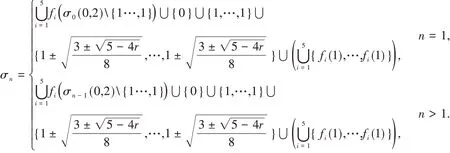
證明 首先，網絡Wn(G)(n≥1)是連通的，所以0是網絡的標準拉普拉斯矩陣Ln的一個特征值.

其次，因為網絡是二分圖當且僅當網絡中不存在奇數環，已知網絡Wn(G)(n≥1)是由許多個六邊形和初代圖G構成，六邊形是偶數環，所以僅通過初代圖能判斷該網絡是否為二分圖，分為兩種情況.當Wn(G)是二分圖時，2是Ln的一個特征值.

進一步，解16(1-x)4-12(1-x)2+1+r≠0，得到于是根據定理2.2，Ln的大部分特征值，除了1和都可以由Ln-1的譜獲得.因此，存在Ln的特征值不能由Ln-1的特征值獲得，它一定是1和此外，Ln-1的每個特征值都會生成Ln的5個特征值，即fi(σn-1),i=1,2,…,5.

最后，整理即證.

3 結論

復雜網絡的特征譜逐漸引起人們關注．網絡的譜是所有特征值的集合，特征值的計算問題是譜研究的重要問題之一.網絡構成越復雜或網絡規模越大，所需計算的難度越高.本文構造了一類自相似網絡——加權迭代六邊形網絡，通過分析和計算得到精確的拉普拉斯譜的結構式.網絡的譜不僅可以用來分析網絡結構，還可以進一步揭示網絡的功能特性，甚至在網絡的動態過程中起到重要作用.