光纖彎曲損耗特性的理論研究

辛春雨

（白城師范學院 機械與控制工程學院，吉林 白城 137000）

0 引言

隨著激光光纖傳輸技術的不斷發展，人們對高功率光纖激光傳輸的光纖損耗的要求逐漸提高.近年來，高功率光纖耦合傳光的輸出功率不斷增加，單根光纖單模輸出的最高功率已達到10 kW.因此，降低高功率光纖耦合傳光的損耗成為人們追求的目標.

對于高功率光纖激光器以及光纖傳輸高功率激光來說，特別是功率達到千瓦量級以上的時候，光纖損耗已經成為限制功率提升的主要因素，光纖的吸收損耗、散射損耗，特別是彎曲損耗受到了人們越來越多的關注.研究光纖的彎曲損耗問題具有很強的現實意義，對制備優良的光纖具有指導作用［1］.近年來，對雙包層光纖激光器中光纖彎曲問題的研究很多，如在20世紀90年代初期，德國研究人員推導了單模光纖的彎曲損耗與彎曲半徑和波長的關系，并對彎曲損耗隨彎曲半徑和工作波長的振蕩變化現象給予了解釋［2］.周情等［3］采用Marcuse理論研究了彎曲損耗隨彎曲半徑、波長和纖芯半徑變化的關系，通過計算機仿真和實驗得出彎曲損耗隨彎曲半徑的減小而增大，隨波長的增大而增大，隨纖芯半徑的增大而增大，高階模式的損耗大于低階模式.本文研究了高功率下，不同光波下彎曲損耗與彎曲半徑的關系.

1 光纖單根彎曲損耗的計算

按照D.Marcuse理論，當彎曲半徑為R時，彎曲損耗系數αb為

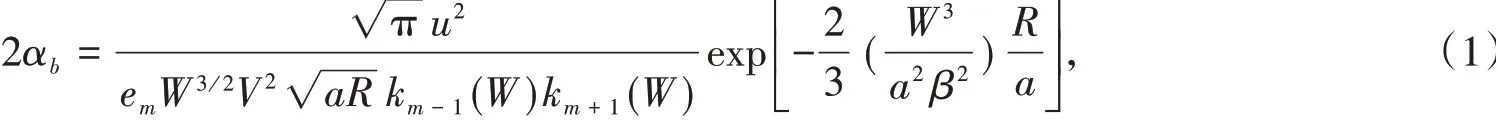
其中：u、W分別為徑向歸一化相位常數和徑向歸一化衰減常數；β為軸向傳播常數；a為纖芯半徑；V為歸一化頻率；km是m階修正貝塞爾函數［4］；em=2（m=0），em=1（m≠0）.

式（1）對每種LPmn模都成立，單模光纖中只傳播LP01模，即

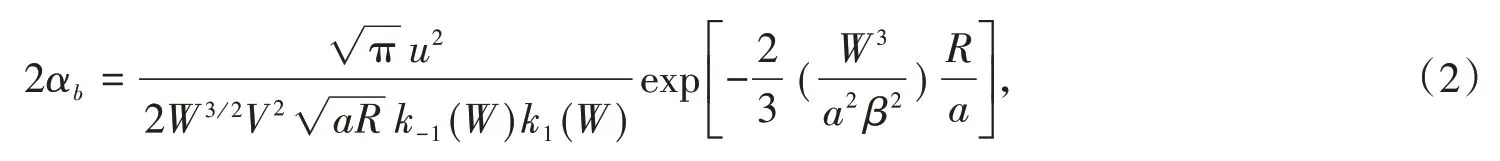
相關參數設置為：纖芯半徑α=14.3μm、n1=1.501、n2=1.5、λ=1.55μm.則當彎曲半徑為20 mm時，單模單根光纖的彎曲損耗為7 dB/km；當彎曲半徑為40 mm時，單模單根光纖的彎曲損耗為0.5 dB/km.

2 光纖束中的彎曲損耗

2.1 平面光波下光纖束中的輸出功率

當彎曲半徑為20 mm和40 mm時，輸出功率計算公式為

其中：Pout為輸出功率；Pin為輸入功率，取值為10 kW；K為光纖束填充率；αb為彎曲損耗系數，取值分別為7 dB/km和0.5 dB/km.輸出功率計算結果如表1和表2所示.

表1 平面光波下彎曲半徑為20 mm時光纖束中的輸出功率

對比表（1）和表（2）的計算數據可知，對于平面光波，在相同條件下，彎曲半徑為40 mm時的輸出功率高于彎曲半徑為20 mm時的輸出功率，即彎曲半徑越大損耗越小.

2.2 高斯光束下光纖束中的輸出功率

當彎曲半徑為20 mm和40 mm時，輸出功率計算公式為

其中：Pout為輸出功率為第一層的輸入功率；P′in為其他層的輸入功率之和.當總輸入功率取值為10 kW，彎曲損耗分別為7 dB/km和0.5 dB/km.輸出功率計算結果如表3和表4所示.

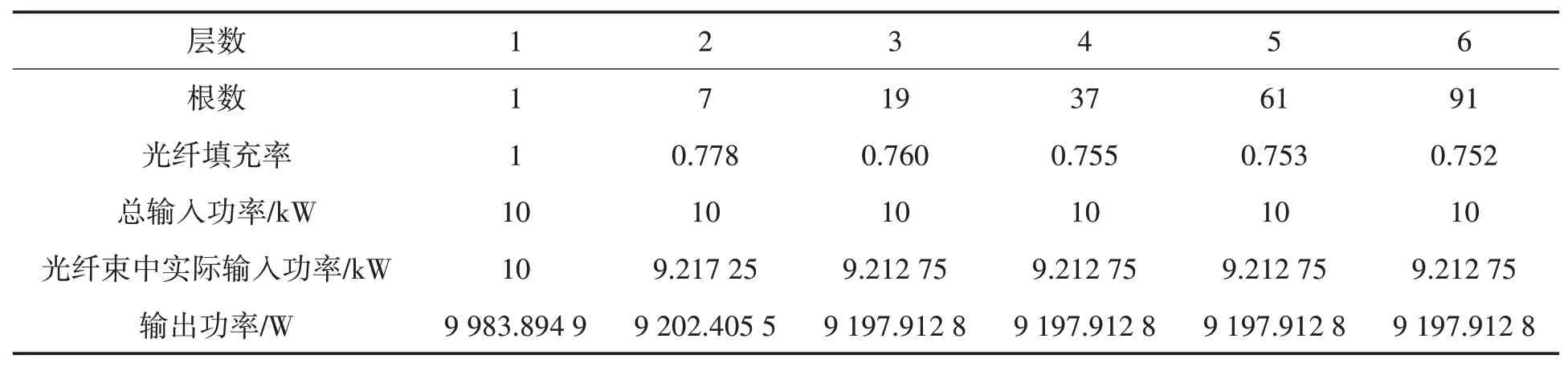
表3 高斯光束下彎曲半徑為20 mm時光纖束中的輸出功率

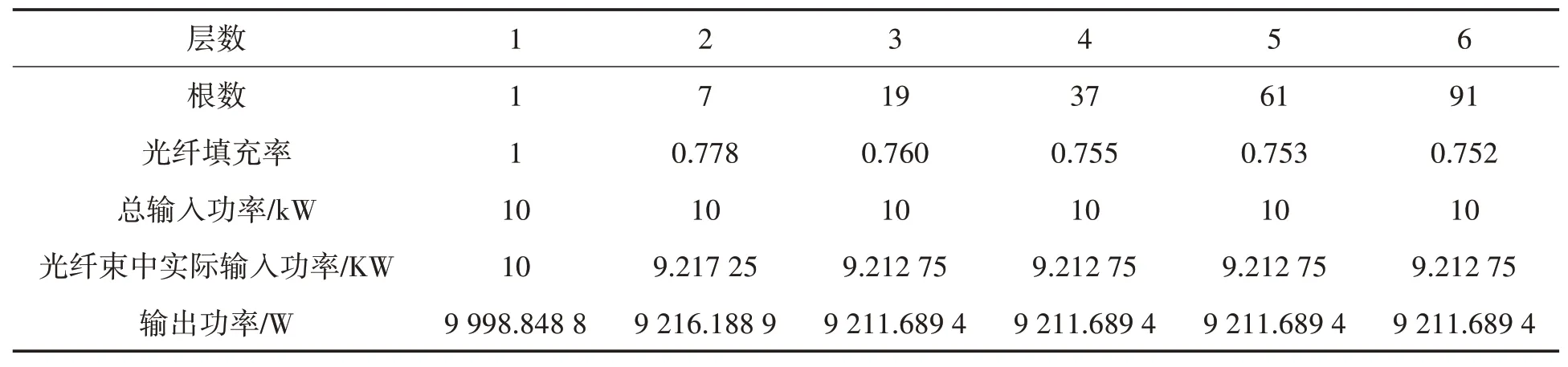
表4 高斯光束下彎曲半徑為40 mm時光纖束中的輸出功率

對比表（3）和表（4）的計算數據可知，對于高斯光束，在相同條件下，彎曲半徑為40 mm時的輸出功率亦高于彎曲半徑為20 mm時的輸出功率，具有與平面光波相同的結論，即彎曲半徑越大損耗越小.對比表（1）和表（3）、表（2）和表（4）可知，在相同彎曲半徑下，高斯光束的輸出功率要大于等于平面光束的輸出功率.

3 彎曲損耗的輸出功率與彎曲半徑的關系

3.1 單根光纖彎曲損耗輸出功率

單根光纖彎曲損耗輸出功率的計算公式為

其中：Pout為輸出功率；Pin為輸入功率；αb為彎曲損耗系數.將實驗數值代入公式（5），計算得出單根光纖彎曲損耗輸出功率，將計算結果用Matlab（2013b）軟件模擬成圖像，如圖1所示.

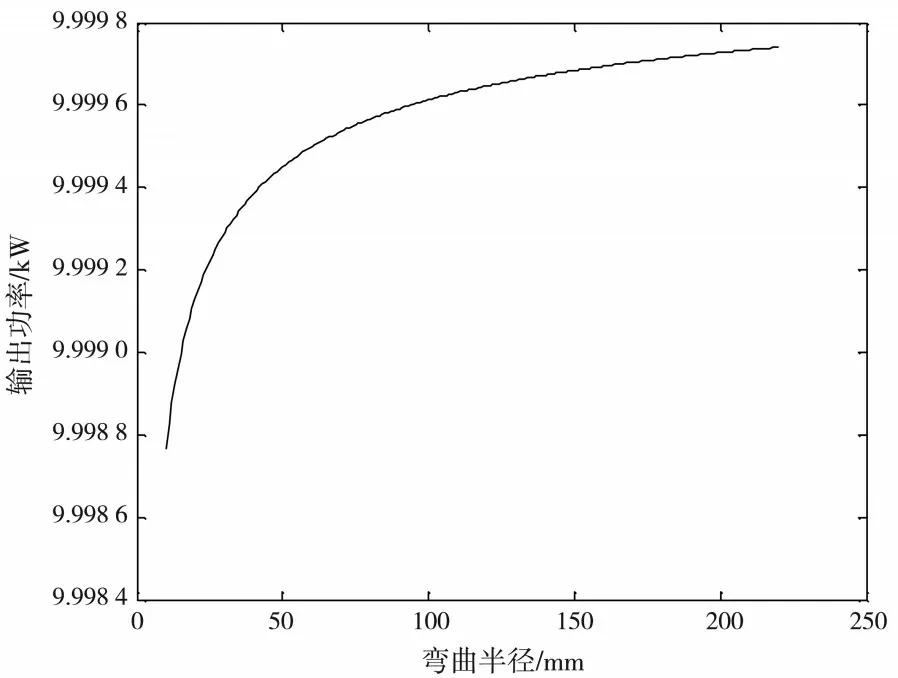
圖1 單根光纖彎曲損耗的輸出功率與彎曲半徑的關系

由圖1可知，對于單根光纖，彎曲半徑越大輸出功率越大，即彎曲損耗越小.

3.2 光纖束中彎曲損耗輸出功率

對于光纖束中彎曲損耗輸出功率的計算，選取2層和5層為例在平面光波和高斯光束下進行計算.

3.2.1 2層情況

（1）平面光波下.將實驗數值代入公式（3），式中光纖束填充率K取值為0.778，計算得出光纖束中2層平面光波下彎曲損耗輸出功率，將計算結果用Matlab（2013b）軟件模擬成圖像，如圖2所示.

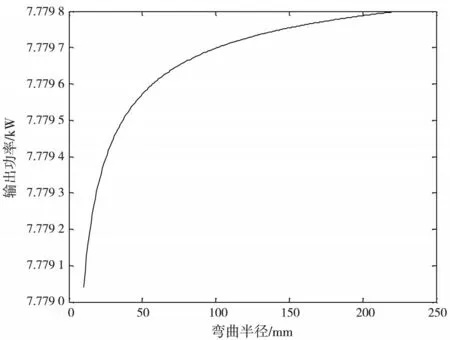
圖2 平面光波下光纖束（2層）彎曲損耗的輸出功率與彎曲半徑的關系

（2）高斯光束下.將實驗數值代入公式（4），式中光纖束中實際輸入功率取值為9.217 25 kW，計算得出光纖束中2層高斯光束下彎曲損耗輸出功率，將計算結果用Matlab（2013b）軟件模擬成圖像，如圖3所示.

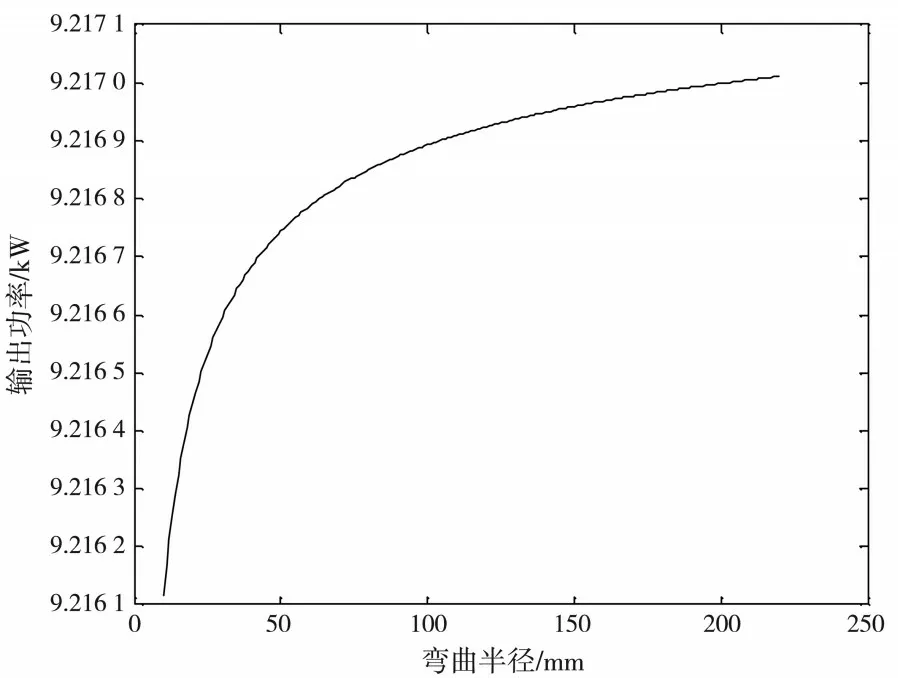
圖3 高斯光束下光纖束（2層）彎曲 損耗的輸出功率與彎曲半徑的關系

3.2.2 5層情況

（1）平面光波下.將實驗數值代入公式（3），式中光纖束填充率K取值為0.753，計算得出光纖束中5層平面光波下彎曲損耗輸出功率，將計算結果用Matlab（2013b）軟件模擬成圖像，如圖4所示.

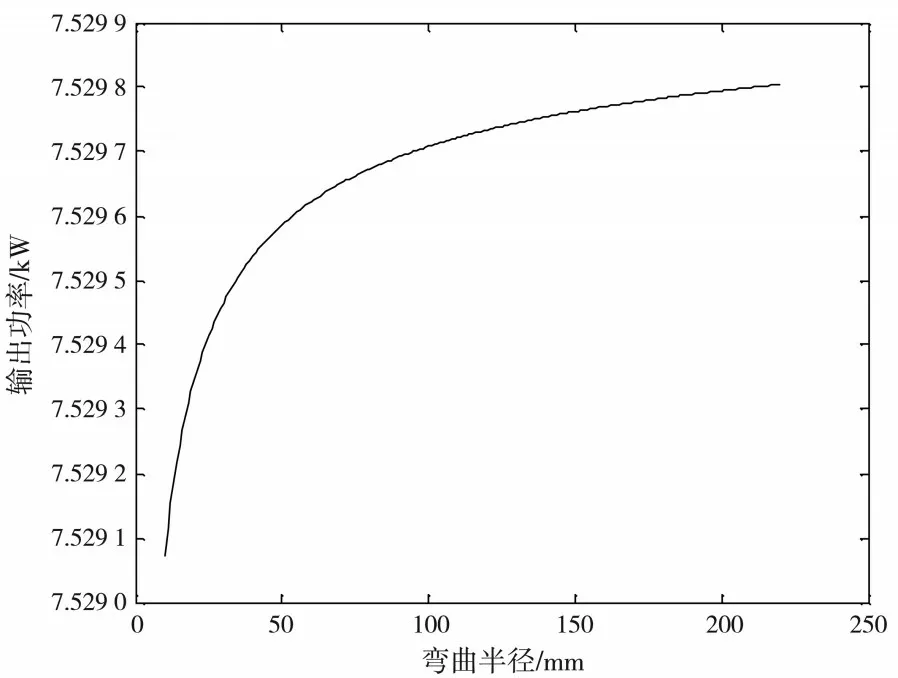
圖4 平面光波下光纖束（5層）彎曲 損耗的輸出功率與彎曲半徑的關系

（2）高斯光束下.將實驗數值代入公式（4），式中光纖束中實際輸入功率取值為9.217 25 kW，計算得出光纖束中5層高斯光束下彎曲損耗輸出功率，將計算結果用Matlab（2013b）軟件模擬成圖像，如圖5所示.

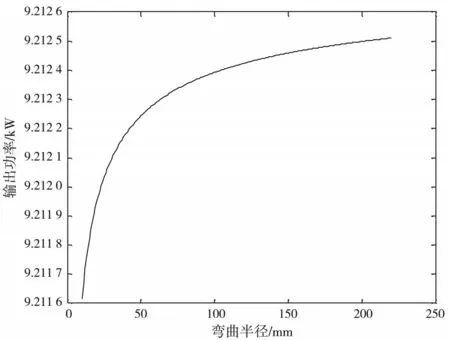
圖5 高斯光束下光纖束（5層）彎曲 損耗的輸出功率與彎曲半徑的關系

由圖（2）—圖（5）可知，在平面光波下（2層和5層）和高斯光束下（2層和5層），彎曲半徑越大輸出功率越大，即彎曲損耗越小；對比圖（2）與圖（3）、圖（4）與圖（5）可知，在相同彎曲半徑情況下，高斯光束輸出功率要大于平面光束的輸出功率.

4 結論

本文按照D.Marcuse的理論，計算了在不同的彎曲半徑、不同光束下相同輸入功率的情況下，輸出功率與彎曲半徑的關系.通過數值計算及分析發現，在相同的高功率輸入情況下，彎曲半徑越大輸出功率越大，即彎曲損耗越小.在相同彎曲半徑的情況下，高斯光束輸出功率要大于平面光束的輸出功率.為了進一步驗證所得結論，又計算了在平面光束和高斯光束下2層和5層彎曲損耗的輸出功率與彎曲半徑的關系，通過曲線關系，進一步驗證了隨著彎曲半徑的增大輸出功率增大的結論.