合理換元 巧妙構(gòu)建
——一道導(dǎo)數(shù)題的探究

山東省菏澤第一中學(xué) 孟麗娟

1 問題呈現(xiàn)

問題[2022年安徽省安慶市高三模擬考試(二模)數(shù)學(xué)試題(理)·12]若存在兩個正實數(shù)x，y使得等式x(2+lnx)=xlny-ay成立，則實數(shù)a的取值范圍是( ).

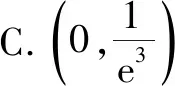
此題以含參的方程為問題背景，利用等式成立創(chuàng)設(shè)情境，進(jìn)而確定參數(shù)的取值范圍.除了參數(shù)a外，還有兩個對應(yīng)的變量x，y，結(jié)合等式的轉(zhuǎn)化并借助對數(shù)運(yùn)算等加以恒等變形，對兩個變量x，y之間的關(guān)系加以合理處理，是切入與解決問題的關(guān)鍵.

2 問題破解

方法1：比值換元法1.

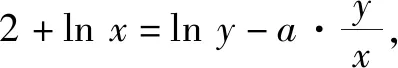
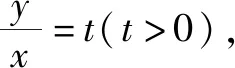
令f′(t)=0，解得t=e3.

當(dāng)t∈(0，e3)時，f′(t)>0，函數(shù)f(t)在區(qū)間(0，e3)上單調(diào)遞增；當(dāng)t∈(e3，+∞)時，f′(t)<0，函數(shù)f(t)在區(qū)間(e3，+∞)上單調(diào)遞減.

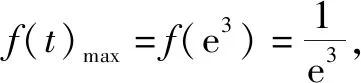
故選擇答案：D.

解后反思：根據(jù)題目條件中對應(yīng)等式的恒等變形，合理分離參數(shù)，巧妙換元，從而構(gòu)建函數(shù)，利用函數(shù)的導(dǎo)數(shù)及其應(yīng)用，通過函數(shù)的單調(diào)性與極值來確定參數(shù)的取值范圍.利用比值進(jìn)行巧妙的換元處理，為構(gòu)建函數(shù)提供條件，從而轉(zhuǎn)化為常規(guī)的函數(shù)問題來分析與處理.

方法2：比值換元法2.

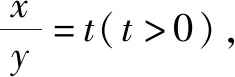
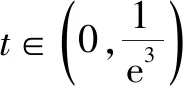
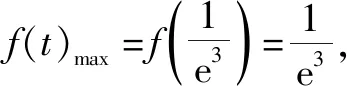
故選擇答案：D.

解后反思：根據(jù)題目條件中對應(yīng)等式的不同視角的恒等變形，也同樣可以進(jìn)行比值換元，雖然換元視角不同，但解題思維一致.抓住常規(guī)思維，合理恒等變形，巧妙分離參數(shù)，正確構(gòu)建函數(shù)，函數(shù)求導(dǎo)處理，單調(diào)極值確定，是解決此類問題中一系列基本的思維步驟與操作技巧.

方法3：多次換元法.

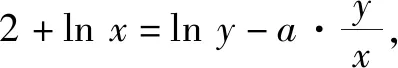
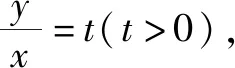
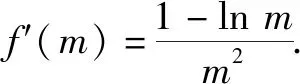
當(dāng)m∈(0，e)時，f′(m)>0，函數(shù)f(m)在區(qū)間(0，e)上單調(diào)遞增；當(dāng)m∈(e，+∞)時，f′(m)<0，函數(shù)f(m)在區(qū)間(e，+∞)上單調(diào)遞減.

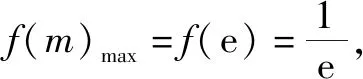
故選擇答案：D.

解后反思：根據(jù)題目條件中對應(yīng)等式的恒等變形，巧妙分離參數(shù)，兩次進(jìn)行換元，其目的是進(jìn)行齊次化處理，進(jìn)而合理構(gòu)建函數(shù)，同樣利用導(dǎo)數(shù)來確定函數(shù)的最值，從而確定參數(shù)的取值范圍.齊次化處理時要求學(xué)生具備較強(qiáng)的觀察能力與數(shù)學(xué)運(yùn)算能力，有時解題中數(shù)學(xué)運(yùn)算量比較大.

3 變式拓展

將原題及其對應(yīng)的解決技巧方法等從視角、深度、廣度等方面加以思考與推廣，才能進(jìn)行多方位的認(rèn)識與應(yīng)用，從而充分體會與挖掘原題的訓(xùn)練與應(yīng)用價值，得到對應(yīng)的變式問題，進(jìn)而進(jìn)一步提升與拓展知識與能力.

變式1若存在兩個正實數(shù)x，y使得等式2x+a·(y-2ex)(lny-lnx)=0成立，則實數(shù)a的取值范圍為( ).

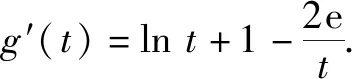
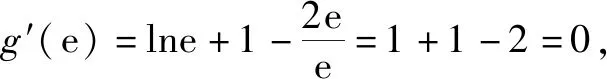
所以g(t)≥g(e)=-e.

故選擇答案：C.

解后反思：根據(jù)函數(shù)與方程的關(guān)系將方程進(jìn)行轉(zhuǎn)化，利用換元法轉(zhuǎn)化為方程有解，構(gòu)造函數(shù)求函數(shù)的導(dǎo)數(shù)，利用函數(shù)極值和單調(diào)性的關(guān)系求解即可達(dá)到目的.合理分離參數(shù)，利用構(gòu)造法和導(dǎo)數(shù)法求出函數(shù)的極值和最值是解決此類問題的關(guān)鍵.

變式2若存在兩個正實數(shù)x，y使等式x+a(y-x)(lny-lnx)=0成立(其中e=2.71828…)，則實數(shù)a的取值范圍是.

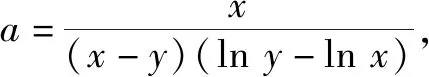
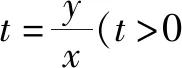
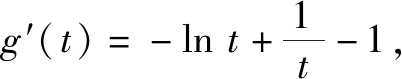
所以當(dāng)t∈(0，1)時，g′(t)>0，函數(shù)g(t)單調(diào)遞增；當(dāng)t∈(1，+∞)，g′(t)<0，函數(shù)g(t)單調(diào)遞減.

故g(t)在t=1時，取得最大值g(1)=0.

解后反思：根據(jù)題目條件合理變換對應(yīng)的等式，巧妙換元與構(gòu)建函數(shù)是破解問題的關(guān)鍵.借助求導(dǎo)來確定函數(shù)的單調(diào)性，進(jìn)而確定對應(yīng)函數(shù)的極值與最值是解決此類問題的目的，為進(jìn)一步解決分離參數(shù)后所對應(yīng)參數(shù)或參數(shù)關(guān)系式的取值范圍提供條件.

4 教學(xué)啟示

(1)通技通法，歸納總結(jié)

涉及等式或不等式恒成立背景下求解參數(shù)取值范圍的問題，“通技通法”就是對相應(yīng)的等式或不等式加以恒等變形與轉(zhuǎn)化，合理構(gòu)建對應(yīng)的函數(shù)，利用函數(shù)的單調(diào)性與極值、最值來求解相應(yīng)參數(shù)的取值范圍.構(gòu)建函數(shù)時，要借助整體換元思維、同構(gòu)思維等.

(2)知識交匯，能力提升

涉及此類等式或不等式恒成立下的參數(shù)取值范圍的問題，經(jīng)常在知識的交匯處加以巧妙設(shè)置，充分考查不同知識點(diǎn)之間的交匯與融合，以及不同知識點(diǎn)與思想方法的綜合與應(yīng)用.解決問題時切入點(diǎn)多，技巧性強(qiáng)，思維方法多樣.通過問題的深入分析與解決，巧妙形成知識體系，清晰解題思維，從而提升學(xué)生理解問題、分析問題與解決問題的能力，拓展數(shù)學(xué)品質(zhì)，培養(yǎng)數(shù)學(xué)核心素養(yǎng).