加強課堂訓練 提升思考能力

江蘇省木瀆高級中學 朱雪民

波利亞認為：“教會學生有目的的思考，是數學教學的基本目標之一.”[1]思考是思維的一種探究活動，是人類對意向信息進行加工的過程，所有思考的進行都存在聯想的參與.數學思考是指從數學的角度，用數學的思維對數學對象進行思考的過程，這種思維方式是形成創新能力的核心.數學抽象、推理與思維是數學思考的靈魂，也是形成數學思想的基礎.高中數學相對抽象，如何立足于當堂訓練，提升學生的思考能力是筆者近些年一直在研究的問題.本文從以下三點展開闡述.

1 加強復述訓練，啟發思考

教學中，不少學生對一些數學知識處于“能意會，卻無法言傳”的狀態，這種情況常導致學生在解題時出現思維模糊、想著想著就跑偏了的現象.而復述是訓練學生思考能力的基本手段之一，它能讓學生清晰思維、明晰解題思路.

所謂的復述是指將所學內容，用自己的語言進行流暢地表達.這種方式能將學生思維的“圖式”呈現出來，讓學生在多次重復的復述訓練中不斷完善并豐富自己的思維結構.相對而言，高中數學有些語言比較拗口、抽象，要讓學生完整地通過自己的語言準確表達出來，實非易事.但為了啟發學生對所學內容的思考，以訓練學生的思維能力，還需要鼓勵學生勤加訓練,長期堅持才能真正達到啟發思維的效果.

例1“曲線的方程”與“方程的曲線”的概念復述.

從字面上來看，這兩個概念異常相近.它們之間到底存在怎樣的區別與聯系？這是本節課教學的重點與難點.為了讓學生徹底弄清這兩個概念，筆者在教學時先與學生共同探討這兩個概念：

在直角坐標系中，若曲線C上的點和某個二元方程f(x,y)=0的實數解建立以下兩點聯系：①曲線上點的坐標全都是該方程的解；②以此方程的解為坐標的點，這些點均為曲線上的點.那么，此方程為曲線的方程，此曲線為該二元方程的曲線.

學生在課堂上雖對此概念有了一定的了解，但若不加以復述或鞏固，不少學生過兩天就開始混淆，理不清楚其中的關系.為此，筆者在當堂課即帶領學生進行復述訓練，以深化學生對這兩個概念的理解.而復述的過程則體現了思維活躍的過程，此過程能有效地啟發學生的思考.

復述：

(1)從定義中的兩個條件來復述

這兩個條件反映了曲線上的點和以方程的解為坐標的點，二者是不多不少，恰合適的關系.從第一個條件來看，曲線上的點不多于方程的解為坐標的點，也就是曲線上的點全都符合條件，沒有一點是例外的；從第二個條件來看，曲線上的點不少于方程的解為坐標的點，也就是說所有符合條件的點均于這條曲線上，沒有遺漏.

(2)從集合的角度復述

將曲線理解為點的集合，記作C；將方程的實數解理解為點的坐標，點集記作F.

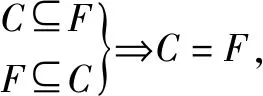
也就是C={(x,y)|f(x,y)=0}.

從這兩個角度進行復述的情況來看，復述訓練能有效地啟發學生的思考，讓學生從自身獨有的思維角度去分析與理解知識的內涵.此過程是內化新知、建構認知體系的重要過程，亦是賦予所學知識價值的過程.

2 強化變式訓練，深化思考

眾所周知，變式訓練是相對于某種范式的變化形式，是深化學生思考，提升解題能力的重要途徑之一[2].變式一般是將簡單的概念、公式、性質等演變成復雜問題的過程，一旦掌握了變式的基本思想，就能掌握解決問題的基本策略與方法.這種訓練方式，對提高學生的辯證思維能力以及思維的自覺領悟能力具有重要影響.

教學中，我們常涉及到的變式有語言、圖形、概念、定理、公式或題目等，不論是哪種變式的應用，均以知識和文化兩大導向為基礎，以實現教學的三維目標為宗旨.我們接觸最多的是試題的變式，即以一道試題為母胎，為了深化其知識的內涵，通過問題條件或結論的變化，呈現出一組新題.通過這組問題的解決，在完善原有認知結構的基礎上深化思考，形成良好的數學綜合素養.

例2已知在數列{an}中，a1=1,an+1=an+1(n∈N*)，求該數列的通項公式.

變式1已知在數列{an}中，a1=1,an+1=an+n(n∈N*)，求該數列的通項公式.

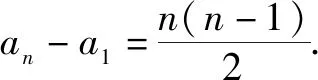
變式2已知在數列{an}中，a1=2n-1,an+1=an+2n-1(n∈N*)，求該數列的通項公式.

解析：形如an+1=an+f(n)的遞推關系式，可采用疊加的數學思想，將問題化歸成等比或等差數列求和.

變式3將原式中an前面的系數變為2，也就是an+1=2an+1，求此時數列的通項公式.

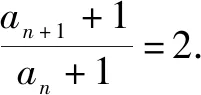
變式4將變式3中的常數改成冪的形式，如an+1=2an-3n，求此時數列的通項公式.

解析1:與變式3類似，把遞推公式變形成an+1+3n+1=2(an+3n)，從而湊配為等比數列{an+3n}，計算可得an=2n+1-3n.

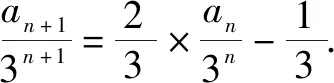
綜上，想要深化學生對知識縱深的理解，變式訓練是最好的方法之一.通過以上變式的應用，學生不僅對此類問題有了更為深刻的認識，在腦海中建構了一系列求解的通項公式，當再次遇到類似問題時，則能舉一反三，順利解題.在此變式訓練的過程中，學生在獲得知識的同時，還形成了良好的思考能力，為各項數學能力的提升奠定了基礎[3].

3 運用感悟訓練，提升思維

曾子有云：“吾日三省吾身.”反思是促進思維成長的利器，是提高人類各項能力的保障.“悟”即深層次的思考與反思，它是學習者思維能力的體現.那么，在數學課上，學生應該從哪些角度去進行感悟呢？筆者認為有以下幾點：

(1)基礎知識的感悟

教學遵循一個循序漸進的過程.課堂教學一般從基礎的概念、定理或公式出發，這些基礎性的知識雖然簡單，但若扣不住它的核心點，不弄清它的發展主線，則無法深刻認識其內涵與外延.而課堂時間又是有限的，有些問題教師并不能講得非常全面、透徹，尤其是在“以學生為主體”的背景下，更多的是教師的點撥與學生的自我領悟.因此，這就要求學生要擁有“悟”的意識，從不同視角去審視與感悟基礎知識，達到知其然且知其所以然的境界.

(2)解題方法的感悟

數學能力的高低可在解題中見分曉，良好的解題方法，為思維指明決策程序，為后期學習中的類比提供保障.對解題方法的感悟，最重要的是要注重思考解題方法的主要特征、基本步驟、技巧等，并將這些內容內化到自己原有的認知結構中，將良好的解題技巧與方法轉化為自己的技能.

(3)數學思想的感悟

解題方法與技巧屬于實施層面的內容，而其背后一般都蘊藏著一定的數學思想，這些數學思想則屬于數學的靈魂.數學思想決定了數學學習的整體策略與方法，是學生真正實現觸類旁通的關鍵因素.因此，教學中應注重加強學生對數學思想方法的感悟.學生一旦領悟了相應的數學思想方法，則能從真正意義上實現以一通百的能力.

總之，提升學習效率是教學的首要任務，訓練學生的思考能力具有重要的戰略意義.作為教師，應結合學情與教學內容，在授學環節，選擇合適的方式進行思考能力的訓練，讓學生在復述、變式與感悟中不斷地提高自身的學習能力與數學核心素養.