某型飛行器氣動參數辨識與彈道仿真

梁明

（中國人民解放軍91851 部隊，遼寧 葫蘆島 125001）

0 引言

隨著計算機技術的不斷發展，模型辨識方法與計算機技術相結合，使得模型辨識精度越來越高，在航天飛行器領域的應用越來越廣泛［1］。本文建立了某型飛行器動力學模型結構，對氣動力辨識輸入參數進行了分析；采用迭代算法得出辨識參數，并對辨識精度進行了分析，認為主要是觀測量測量誤差、物理幾何參數誤差影響辨識精度。模型辨識的難點在于參數精度的分析和確認，本文在初步分析影響精度主要因素的基礎上，將辨識得到的氣動參數帶入彈道仿真程序進行仿真驗證。

1 建立某型飛行器動力學模型

1.1 理論分析

在建立模型過程中，將某型飛行器視為運動剛體，其在空間的運動可以分解為3 個線位移和3 個角位移，用6 自由度來進行描述，采取輸入激勵信號激發某型飛行器運動模態，從而辨識出該型飛行器的相關氣動參數［2］。

某型飛行器助推器工作時間比總飛行時間要短的多，一般只有3～4 s，但助推器的推力很大，通常助推器推力產生的縱向過載可達15～18g，在助推器推力持續作用時，空氣動力的影響幾乎可以忽略，且助推段很難獲得滿足參數辨識要求的響應參數［3］，因此本研究中不考慮助推器的推力。在上述條件下，某型飛行器6 自由度動力學數學模型為［4］

式中：Wxd、Wzd為風速在地面座標系的分量，Wxd=WcosψW，Wzd=-WsinψW，ψW為風向角。

氣動系數的模型應根據某型飛行器氣動外形的特點來確定［5］，一般情況下可表示為

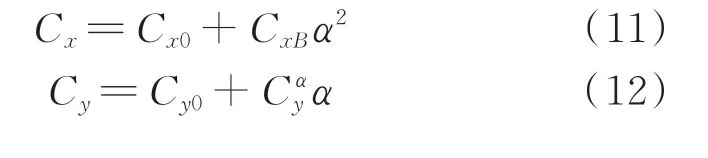
以上方程再加上控制方程就成為一個完整的方程組。某型飛行器的調節規律方程通常可表示為［6］

從調節規律的方程還可以看出，某型飛行器3 個通道的控制是互相獨立的，正常飛行情況下，可以將6 自由度動力學數學模型，簡化為縱向和側向2 個3 自由度的動力學模型［8］。

1.2 辨識輸入數據

1）導彈的結構參數：導彈質量m，轉動慣量Jx、Jy、Jz，導彈質心XT、YT，參考面積S，平均氣動弦長bA，參考長度l，傳感器的安裝位置等；

2）外彈道測量參數：導彈速度V、飛行高度h等；

3）氣象測量參數：密度ρ（若密度無實測值可根據飛行高度計算）、風速W、風向角ψW等；

4）內彈道測量參數：舵偏角δx、δx、δx，導彈姿態角ψ、?、γ，導彈轉動角速度ωx、ωy、ωz，導彈軸向、法向、側向過載Nx、Ny、Nz，發動機推力R，導彈攻角α，側滑角β等。

2 迭代算法

采用牛頓-拉夫遜迭代公式［9］

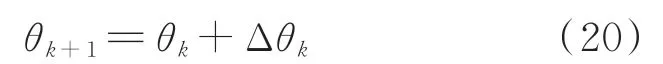
式中的d修正量Δθk可由下列線性代數方程組計算［10］：

具體迭代過程為根據某型飛行器理論計算結果，給出待估氣動參數的初值θ0，由狀態方程、觀測方程和靈敏度方程積分出某型飛行器的狀態值x、觀測值y和靈敏度陣；然后，解線性代數方程組求出Δθ0，再以θ1=θ0+Δθ0代替原來的θ0，重復以上計算過程，每迭代一次都需要計算似然準則函數Jk和Jk/Jk-1［11］。當時，則認為迭代收斂，此時的待估參數θk，即為所求的氣動參數，一般情況下取ε=0.01［12］。

3 辨識精度分析

影響氣動參數辨識精度的因素較多，歸納起來有以下幾個方面：

1）觀測量的測量誤差。觀測量的測量誤差是影響辨識精度的重要因素［13］。利用飛行試驗數據進行參數辨識時，觀測量一般取導彈轉動角速度ωx、ωy、ωz，姿態角ψ、?、γ，導彈軸向、法向、側向過載Nx、Ny、Nz，導彈攻角α，側滑角β。分別由安裝在彈體內部的角速率傳感器、角位移傳感器、過載傳感器、攻角傳感器及側滑角傳感器獲得。通過遙測傳感器獲得時，零位漂移、死區、安裝誤差不可避免，但選擇高精度的傳感器可以使誤差減小，為滿足氣動參數辨識的需要，遙測傳感器應滿足如下要求：

（1）噪聲強度系數不高于1%；

（2）角位移傳感器的零位漂移速度應小于每分鐘0.1°，角速率傳感器的零位漂移小于峰值的0.2%，過載傳感器零位漂移應小于峰值的1.0%；

（3）傳感器的標定誤差應小于0.3%；

（4）閉環飛行試驗中，角速率、角位移、過載傳感器的死區分別應在0.03（°/s，（°），g）的范圍內；

（5）角速率傳感器安裝角的偏移度要小于0.1°，過載傳感器安裝角的偏移度要小于0.2°，過載傳感器質心位置及安裝位置誤差要小于3.0 mm。

2）幾何和物理參數的誤差。幾何參數包括特征長度、面積，物理參數包括慣性力矩、動壓、質量，這些量中任何一個量值存在的誤差，都會對氣動參數估值產生相同的誤差［14］。

4 參數辨識應用

4.1 可辨識性分析

若右端某一項遠小于左端，則該項是不可辨識的；若左端接近于零，則該項也是不可辨識的，其余類同。

數據取自該型飛行器6 自由度85～86 s 的內、外彈道數據，數據包括：光測數據t、V、h、θ、ψc，遙測采樣數據ωx、ωy、ωz、Nx、Ny、Nz、δx、δy、δz、α、β，彈體結構參數l、bA、S、m、Jx、Jy、Jz，氣象數據ρ、W、ψW等。

為了分析這段數據的可辨識性，將動力學方程的各項分別逐項計算，結果見表1—表3。可以看出與各項的數量級相當，這表明縱、側向氣動系數均可進行辨識，可以采用6 自由度參數辨識的基本方程組進行辨識，表中數據還表明阻尼參數的數量級較小，會有較大的辨識誤差［16］。

表1 辨識數據x表Tab.1 x table of identification data

表1 辨識數據x表Tab.1 x table of identification data

表2 辨識數據y表Tab.2 y table of identification data

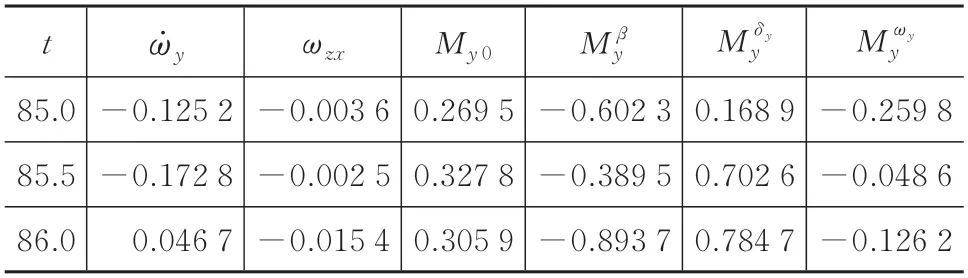
表2 辨識數據y表Tab.2 y table of identification data

表3 辨識數據z表Tab.3 z table of identification data

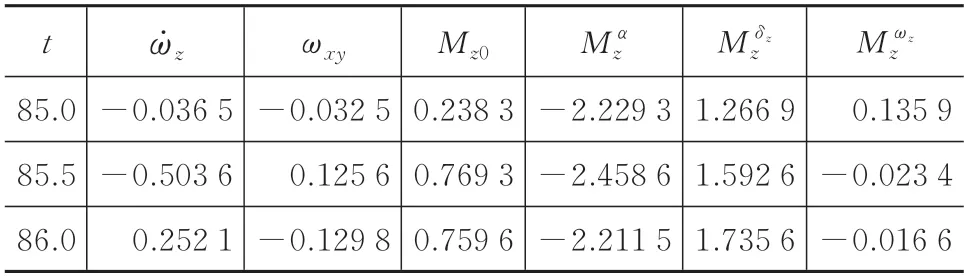
表3 辨識數據z表Tab.3 z table of identification data

4.2 辨識結果

采用極大似然法，對仿真數據采取參數辨識的基本方法進行辨識［17］。

狀態變量為

觀測量為

待估參數為

共辨識出21個氣動系數，辨識結果見表4～表7。

表4 辨識結果（1～5）Tab.4 Identification results（1～5）

表6 辨識結果（11～16）Tab.6 Identification results（11～16）

表7 辨識結果（17～21）Tab.7 Identification results（17～21）

辨識得到的氣動參數為計算飛行器彈道導彈飛行力學所需要的升力、阻力、側向力，俯仰、滾轉、偏航力矩系數及其對迎角、側滑角、舵偏角的偏導。辨識得到這些氣動參數之后，便可以對導彈的彈道進行仿真分析［18］。

5 辨識模型的彈道仿真

通過對該型飛行器控制系統和動力系統進行辨識，得出了部分模型辨識參數，下面驗證這些實辨參數模型。

根據理論模型編寫彈道仿真程序，可有效地計算該型號飛行器的控制彈道，并經過多次實彈飛行試驗驗證。驗證結果表明，該理論模型精度較高，滿足要求。

將實辨模型代入該型飛行器彈道仿真程序，替換原來的理論模型，進行彈道仿真計算。從仿真結果看，彈道變化平穩，與試驗數據吻合較好，誤差符合規定的范圍，通過本方法得到的氣動力參數精度已滿足工程實際需要，實際辨識模型參數具有可信性［19］。Y方向仿真彈道如圖1 所示，該彈道反映了某型飛行器初始正常爬高，按照預定程序下滑、穩定平飛、91 s 開始規避爬升、躍過目標艦后下滑入水自毀。

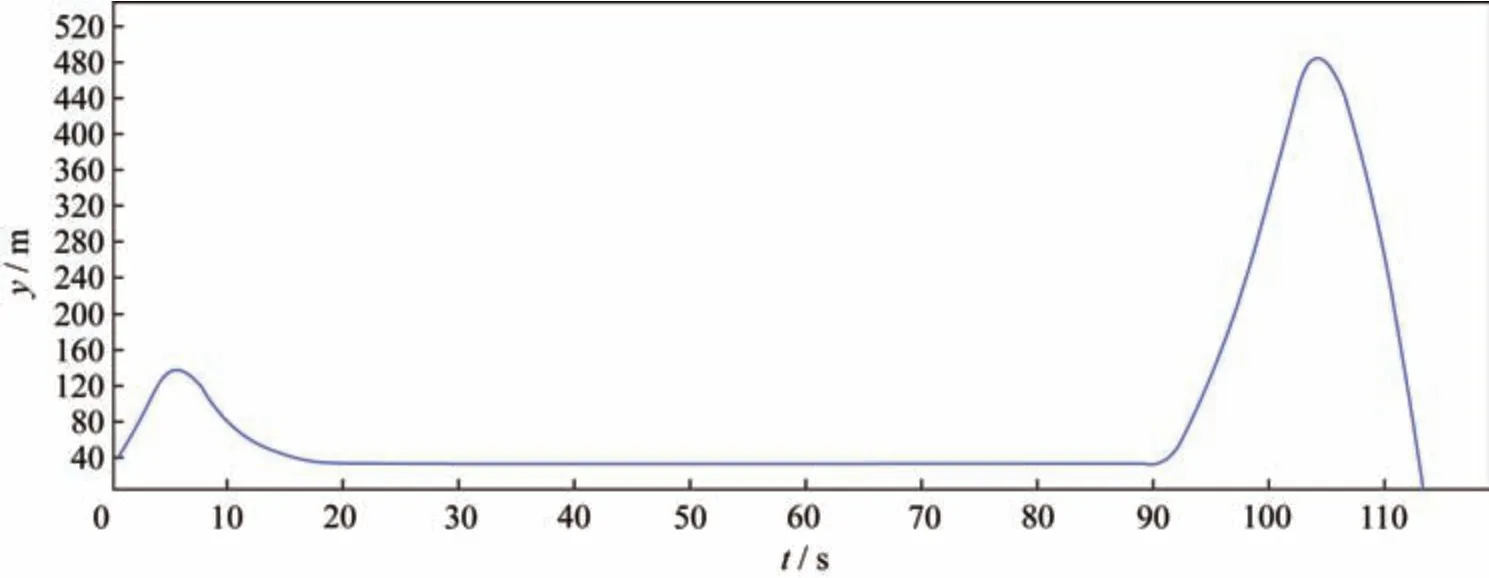
圖1 Y 方向仿真彈道Fig.1 Simulation ballistics in the Y-direction

等效飛行高度曲線如圖2 所示，該曲線反映了某型飛行器高度通道輸出變化規律，從0～90 s 高度通道正常輸出高度表測量高度，90 s 以后輸出固定高度電平，從而完成安控規避。X方向仿真彈道曲線如圖3 所示，該曲線反映了該型號飛行器縱向位移平穩。

圖2 等效飛行高度仿真Fig.2 Equivalent flight altitude simulation

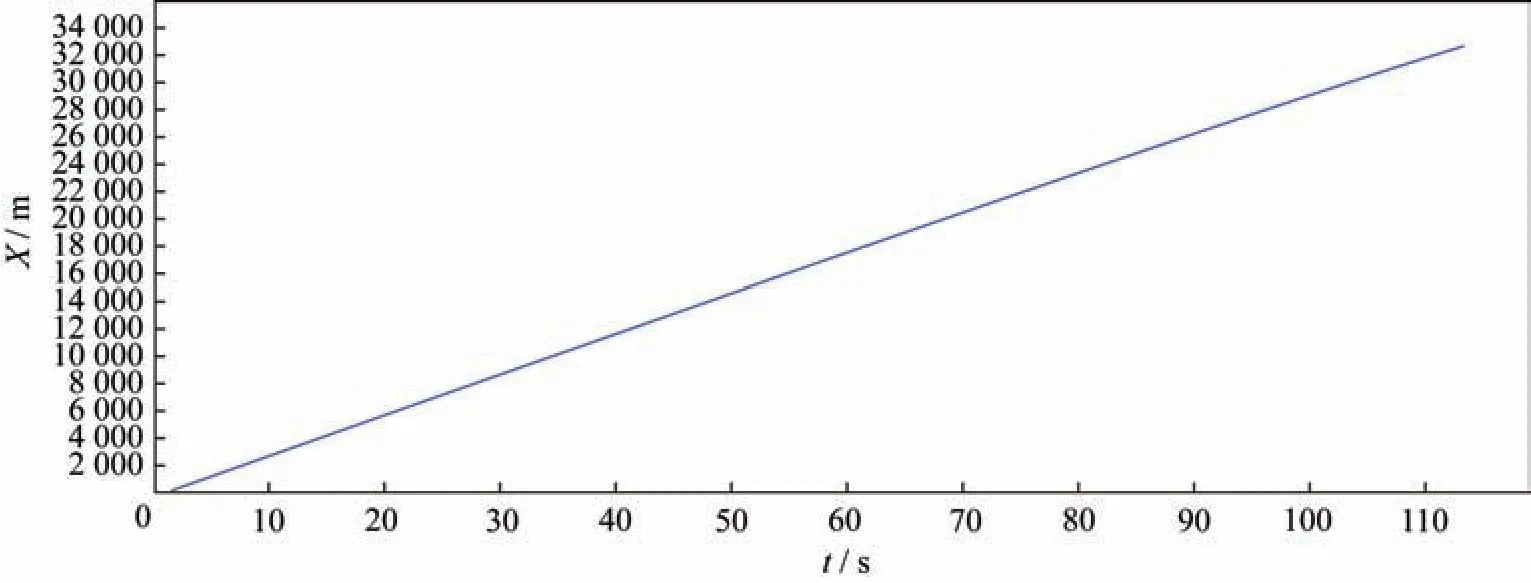
圖3 X 方向仿真彈道Fig.3 Simulation ballistics in the X-direction

1～4 舵機仿真曲線分別如圖4～圖7 所示，4 條仿真曲線反映了某型飛行器舵機系統的變化規律，這4 個舵機系統動作對稱性好，響應速度快，滿足該型飛行器控制要求［20］。

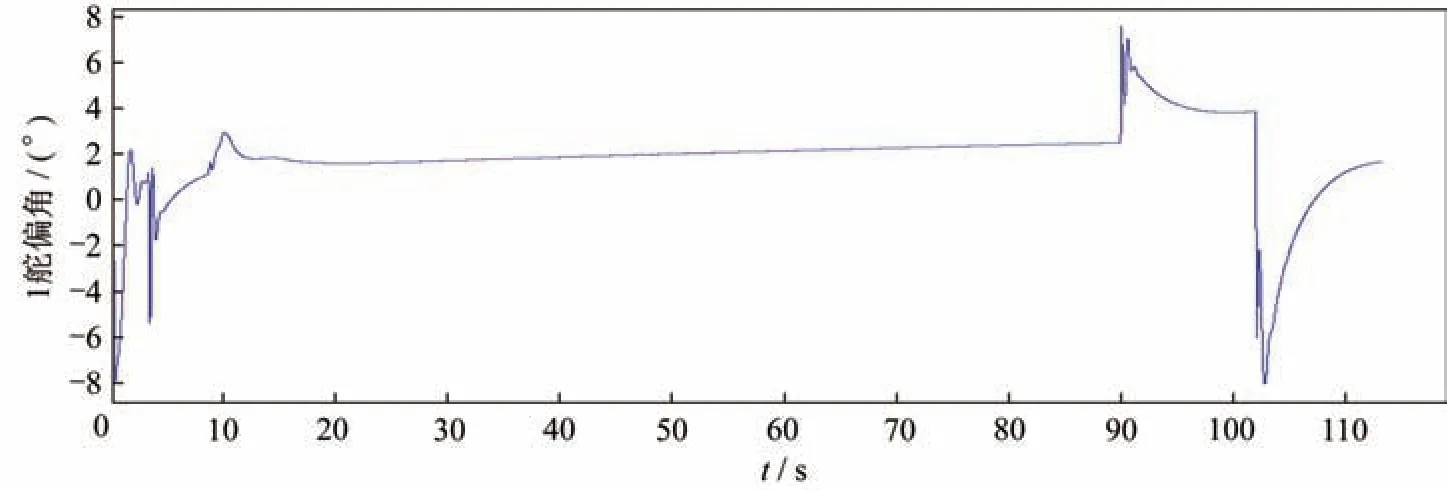
圖4 1 舵機仿真曲線Fig.4 Simulation curve of Servo 1

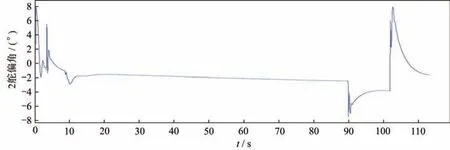
圖5 2 舵機仿真曲線Fig.5 Simulation curve of Servo 2

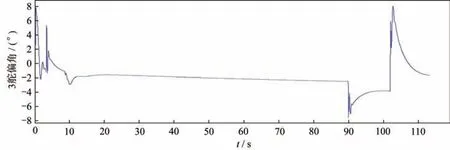
圖6 3 舵機仿真曲線Fig.6 Simulation curve of Servo 3

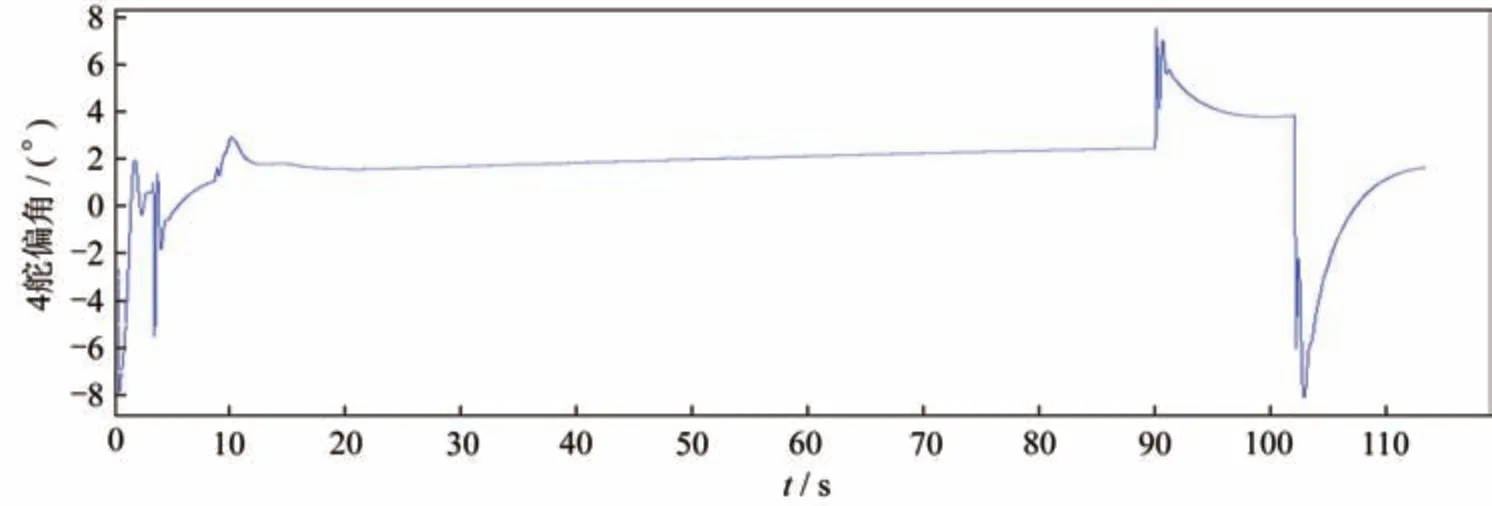
圖7 4 舵機仿真曲線Fig.7 Simulation curve of Servo 4

6 結束語

本文介紹了一種飛行器氣動模型參數辨識方法，利用該方法進行了飛行器的典型氣動參數辨識，并將辨識得到的氣動數據代入彈道仿真程序中進行驗證。驗證結果表明，該氣動參數得到的彈道與實際情況吻合程度高，辨識精度較好。同時作為一種工程方法，該氣動參數辨識方法使用較為方便，計算耗時較少，適合于多種工程場景，在工程領域有廣泛的應用前景。