圓域上二重積分數值計算的一種構造方法
婁汝馨 ,崔 嵬
(1.保定學院 數據科學與軟件工程學院,河北 保定 071000;2.天津師范大學 數學科學學院,天津 300387)
二重數值積分在科學計算中具有非常重要的作用,關于矩形域上的數值積分方法已有一些研究成果,張凱院給出了單位正方形區域上的一個數值求積公式[1],邢會超等給出了矩形域上的梯形求積公式、拋物線求積公式、復化梯形求積公式和復化拋物線求積公式[2],陳亞婷等把一個區間[a,b]上具有7次代數精確度的求積公式應用到矩形域,并給出了截斷誤差估計[3].而對于不規則區域的二重數值積分的研究相對較少,何洪英等給出了坐標平面上的兩組通用計算公式,并通過數值算例給出了八類積分區域的分割方法[4],但沒有給出具體節點以及節點處函數值的權重系數,朱振廣則用Simpson方法和三點Gauss公式構造出復雜區域上的一種二重積分計算方法[5].
本文將針對圓域上的二重積分,給出區域的分割方法,確定節點,并建立數值積分公式.
1 預備知識
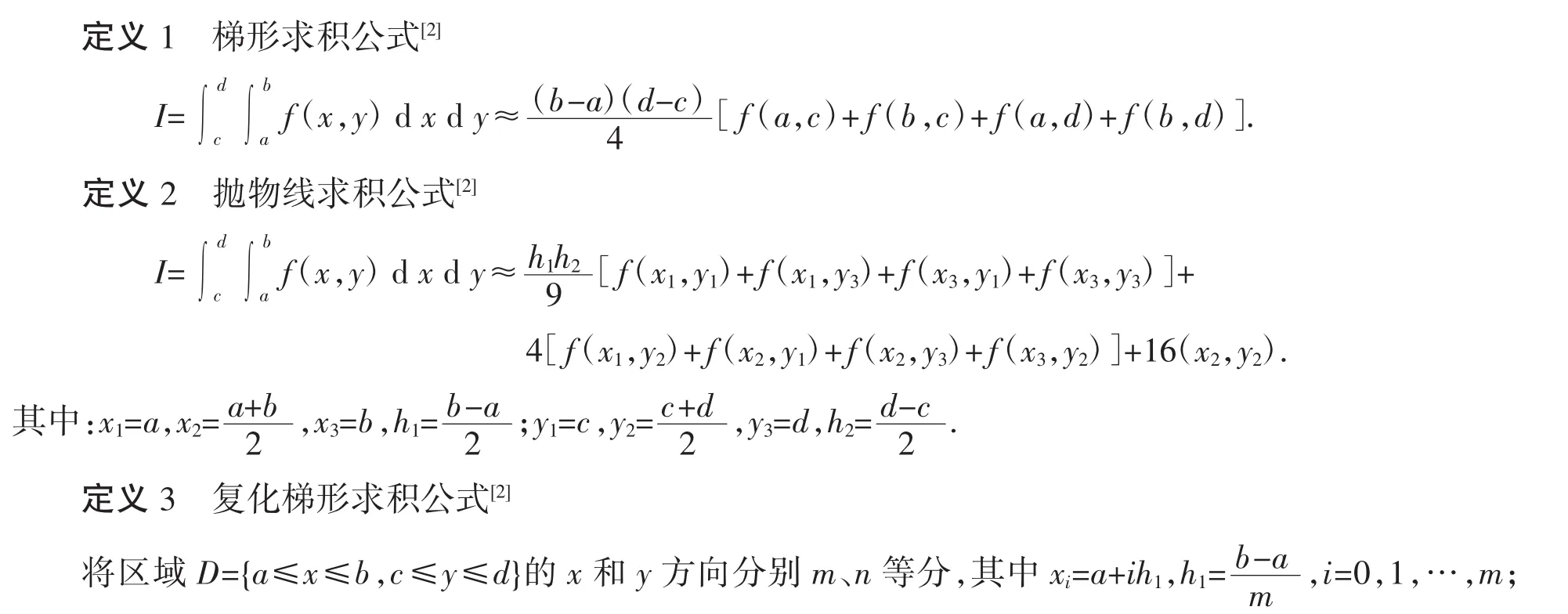

2 圓域上的二重積分數值計算
圓形區域上的數值積分,沒有現成的公式可以套用,下面嘗試將圓域分割成矩形域進行近似計算.對于圓的切分,最直觀的想法是做過圓心的若干直線將其等分.下面以圓心位于原點、半徑為r的圓域為例進行說明.
2.1 圓形區域的分割
首先利用坐標軸將其四等分.過圓與坐標軸的交點,做平行于坐標軸的直線,將圓域“罩起來”,此記為第一次分割(見圖1),此時整個區域是由2個矩形組成,規定x軸上方的為D1,x軸下方的為D2,此時分割圓弧所對的圓心角為α1=2-1π,可以把圓域上的積分近似用矩形域來代替,但此時矩形域會多出很大一部分,誤差明顯很大.

圖1 第一次分割
為了減小誤差,繼續分割,對圓周八等分.此時整個區域由4個矩形組成,圓弧所對的圓心角為α2=2-2π,規定由上到下的小矩形區域分別是D1、D2、D3、D4,此次分割記為第二次分割(見圖2),每個區域的范圍是:
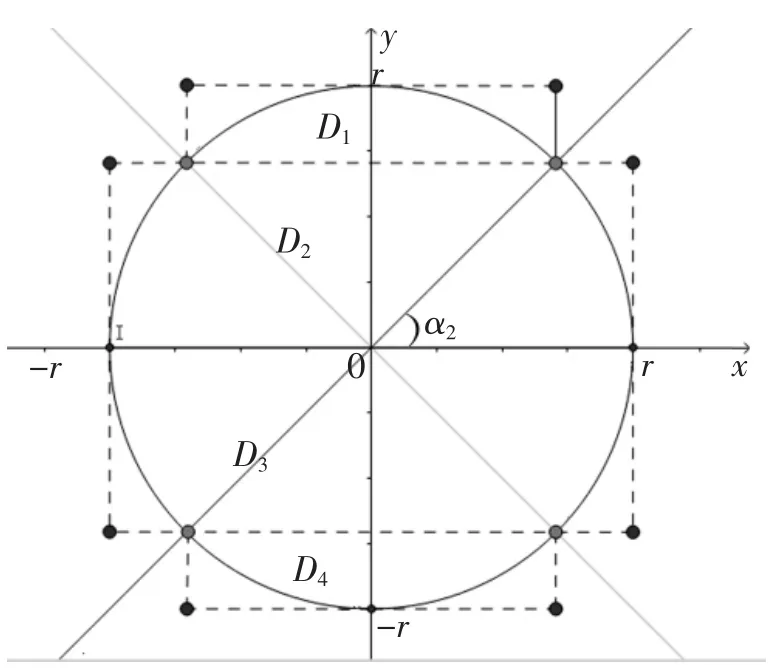
圖2 第二次分割
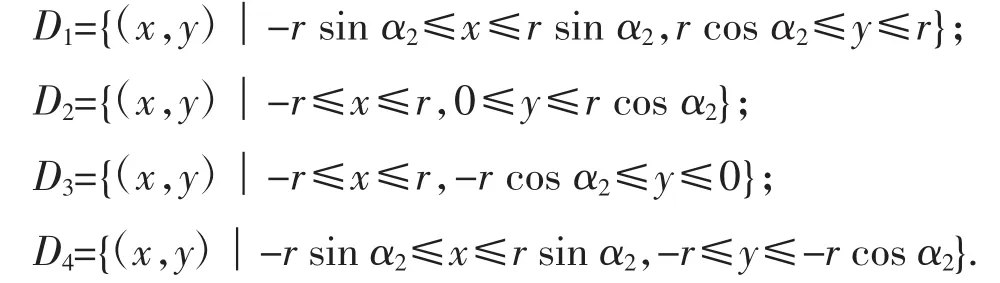
區域誤差有所減小,繼續進行第三次分割(見圖3),此時整個區域由8個矩形組成,圓心角為α3=2-3π,每個區域的范圍是:

圖3 第三次分割
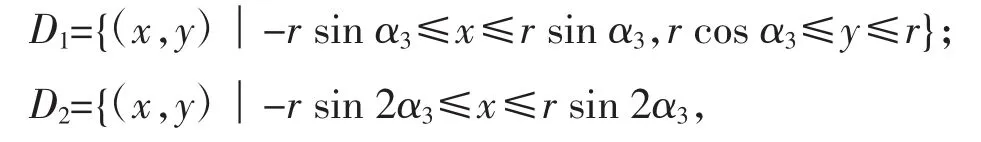

隨著分割的次數增加,誤差逐漸減小,分割一直持續下去,到第n次分割,此時把圓形區域轉換成了2n個矩形區域,圓心角為αn=2-nπ,每一個區域的范圍如下:
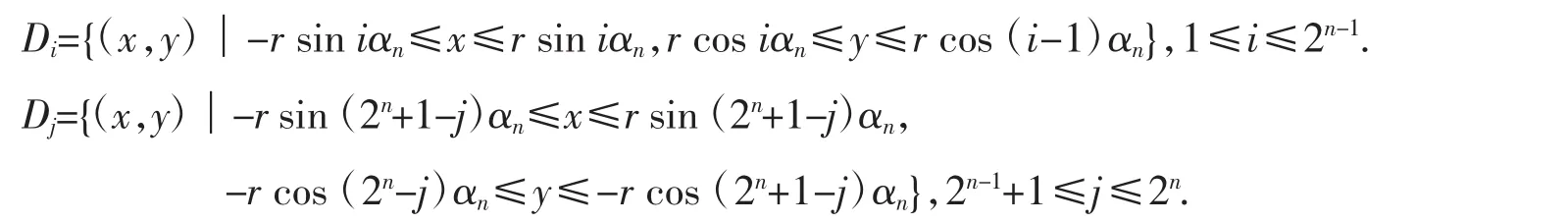
2.2 圓域上的梯形求積公式
由二重積分的可加性,圓域D={(x,y)|x2+y2≤r2}上的積分可近似等于每個小矩形域上的積分之和,即
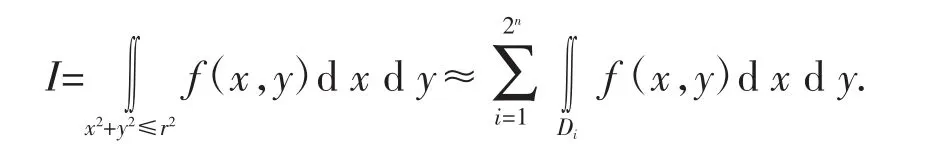
當把圓域n等分時,記Di={(x,y)│xi≤x≤xi+1,yi≤y≤yi+1},可知:xi=-r sin iαn,xi+1=r sin iαn,yi=r cos iαn,yi+1=r cos(i-1)αn.在每個小區間上使用二重積分的梯形求積公式,得
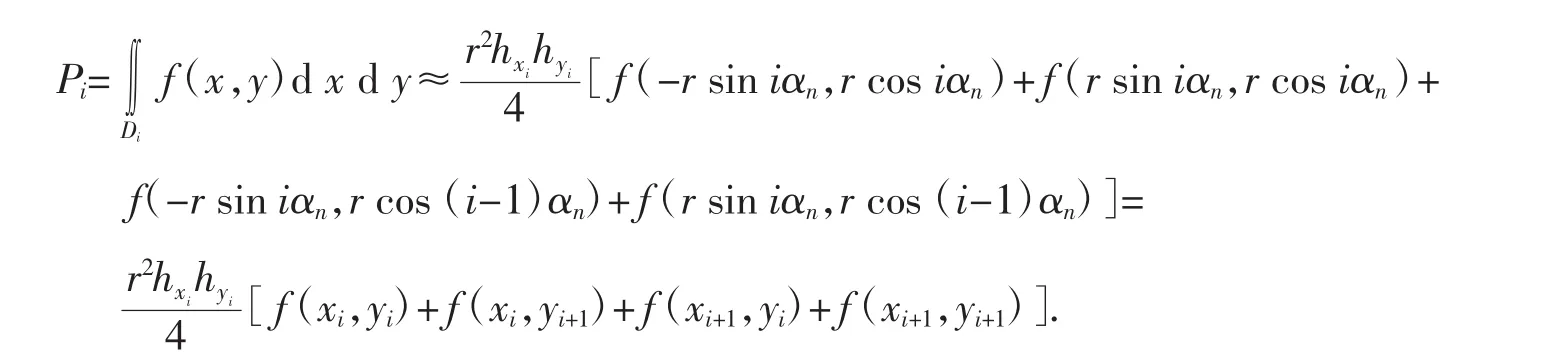
其中 1≤i≤2n-1,i∈Z,且 hxi=2 sin iαn,hyi=cos(i-1)αn-cos iαn.
同理可得,
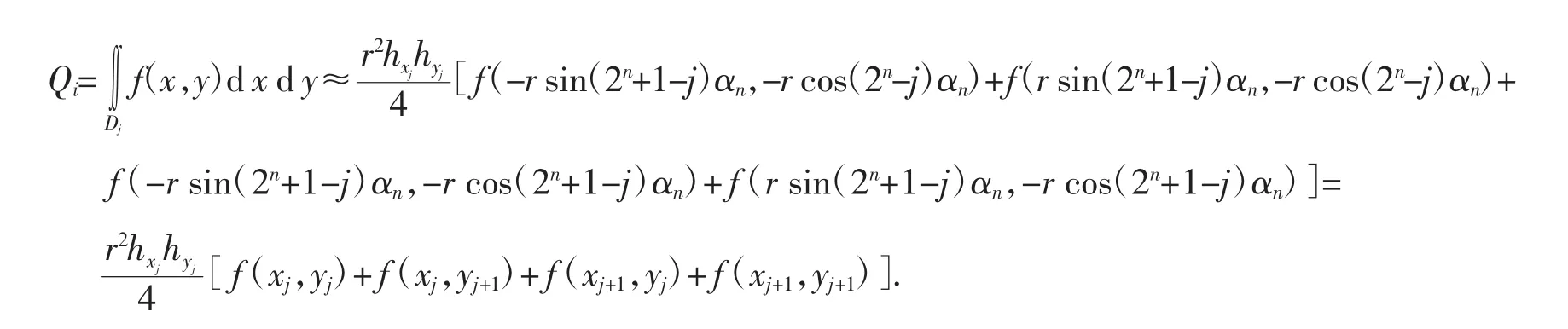
其中 2n-1+1≤j≤2n,j∈Z,且 hxj=2 sin(2n+1-j)αn,hyj=cos(2n-j)αn-cos(2n+1-j)αn.把上面兩部分區域的積分累加,得圓域上的梯形求積公式:
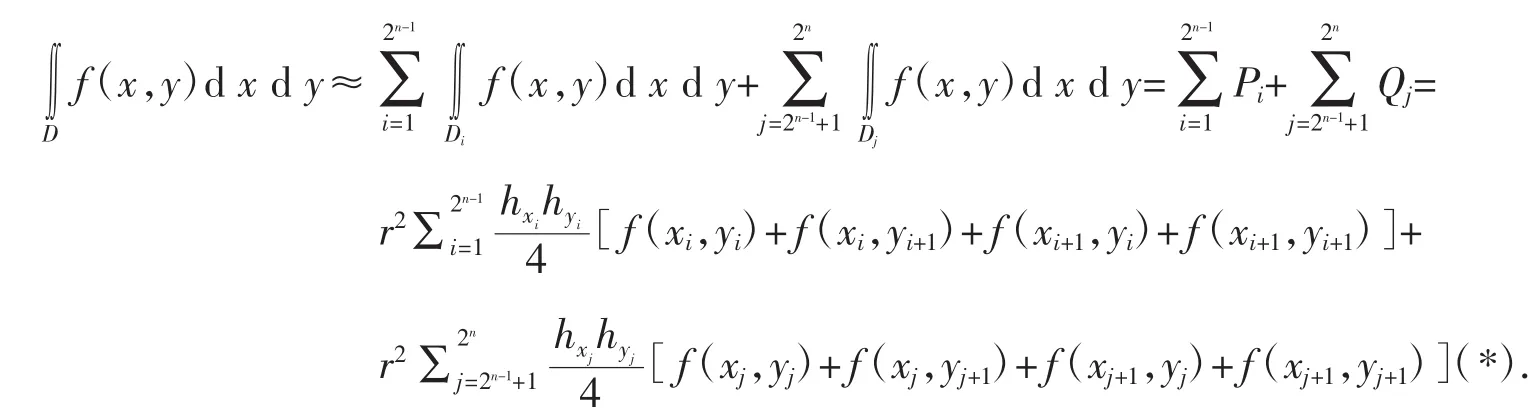
這時,hxi、hyi、hxj、hyj是不依賴于函數 f(x,y)和區域半徑 r的常數,可以事先計算出來.
2.3 圓域上的復化梯形求積公式
觀察圓域上的梯形求積公式(*)不難發現,求積公式的本質為節點處函數值的加權求和,而梯形求積公式的節點大都分布在圓域的邊界線附近,如果被積函數是關于x和y的單調函數,勢必會引起較大的誤差,為了緩解由此帶來的影響,可采取加密節點的策略,即在每個小矩形域上使用復化梯形或復化拋物線求積公式進行計算.
由于在圓域分割為矩形域的過程中,y軸方向已經進行了多次分割,可以只考慮在x軸方向上加密節點即可.
當把圓域分割n次時,圓域被近似分成2n個矩形區域(分割圖可參考圖3),并且D1與D2n,D2與D2n-1,…,D2n-1與D2n-1+1均關于x軸對稱,對x軸分割后分點各自對應相等.下面不妨以x軸上方的區域Di為例來說明復化求積的思想.Di=({x,y)│-r sin iαn≤x≤r sin iαn,r cos iαn≤y≤r cos(i-1)αn},由于-r sin iαn≤x≤r sin iαn,把區間[-r sin iαn,r sin iαn]m 等分,分點為.
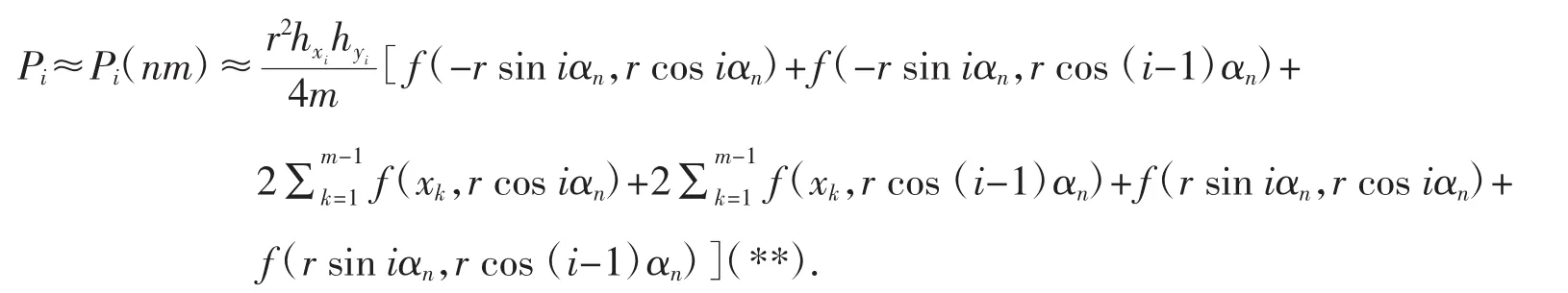
其他區域做類似變換即可.
3 數值算例
計算二重積分?x2+y2≤1e-(x2+y2)d x d y.
解:1)計算積分精確值.做極坐標變換,得
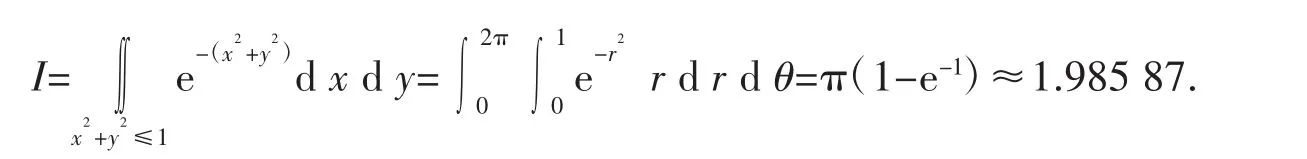
2)利用復化梯形求積公式(**),取 n=10,m=1,2,4,6,8,10(m=1 即為梯形求積公式)分別計算出近似值和誤差的絕對值見表1.

表1 復化梯形求積公式計算結果
3)結果分析:由表1可以看到,當給定n值,m由小逐漸增大的過程中,計算值的誤差逐漸減小,并最終趨向于零,誤差隨m變化的趨勢見圖4.

圖4 誤差走勢
從計算結果可以看出,用上述復化梯形求積公式求解圓域上的二重積分具有理論意義和應用價值.
本文給出了用復化梯形求積公式求圓域上的二重積分的構造方法以及結果,并通過數值算例展示了誤差的變化趨勢,但還需進行嚴格的理論證明.未來,筆者將繼續深入研究數值積分,嘗試采用不對等剖分[6]或者分離截斷誤差與舍入誤差的策略[7]提高算法的精度,并把數值積分方法推廣到更一般的不規則區域.

