裝備維修器材預儲點選址與預置運輸配送組合優化方法

曹軍海，張闖，李延通，郭一鳴，郭慶義

(1.陸軍裝甲兵學院 裝備保障與再制造系，北京 100072；2.大連海事大學 航運經濟與管理學院，遼寧 大連 116026；3.65316部隊，遼寧 大連 116300)

0 引言

裝備維修器材的預儲預置，是保障作戰部隊在戰爭初期快速獲得器材供應的重要手段，是提高裝備維修器材保障效率和部隊持續戰斗力的關鍵之一。美軍在海灣戰爭、伊拉克戰爭等21世紀以來的幾次局部戰爭中，通過海上、陸上等預儲預置力量，實現了裝備和物資的快速部署，促進了部隊戰斗力的快速生成，對后續作戰行動起到了促進作用[1]。當前，我國陸軍正在進行深刻改革，從區域防衛型向全域機動型轉變。面對當前我周邊復雜備戰形勢，有必要在主要戰略方向預先配置一定規模的裝備維修器材，避免保障任務初期出現保障難、保障慢的問題，提高戰時部隊部署效率，快速形成戰斗力和保障力。

針對戰時預置儲備問題，一些學者已經進行了研究。林勇等[2]對美國陸軍預置儲備情況進行系統梳理，并結合我國陸軍實際提出了建設啟示。李守耕等[3]分別對邊境地區、島礁、海外基地和海上艦船4種戰備物資預置方式進行研究，并提出可行方案。王耀等[4]針對島嶼、邊境和海外等3種作戰環境下后勤戰備物資預置儲備進行總體設計。在戰時軍事物流的文獻中，張巍等[5]研究了戰時前沿補給基地的選址問題。王申坪等[6]針對戰時裝備倉庫選址問題，提出了基于兩階段的廣義最大覆蓋模型，并針對某次演習任務中裝備倉庫的選址進行了仿真分析。呂游等[7]研究了戰時物流配送路徑規劃問題，姜大立等[8]對戰時不確定環境下的軍事運輸動態路徑規劃問題進行了研究。

從當前已有文獻來看，一方面，對裝備物資預置儲備的文獻大多集中于總體設計和方案研究，少有對主要戰略方向預儲點選擇和戰前裝備物資快速預置等問題的優化方法研究。另一方面，戰時軍事物流的文獻中，大多研究裝備物資倉庫或基地的選址問題，或運輸配送問題，而很少將二者作為一個問題同時考慮。事實上，設施(倉庫)選址和基于設施位置的運輸配送二者緊密相關，設施選址是運輸配送的前提和基礎，后期運輸配送是設施選址的目的和后續。傳統的優化方法將二者作為獨立問題分別研究，首先確定設施選址方案，當預置任務開始時，基于前期選址確定的設施位置，進行需求分配和運輸保障。這種模式無法保證其方案的全局最優，與信息化戰爭中對裝備器材保障的精確、高效等需求不相適應。為了獲得全局最優的保障方案，需要將二者進行有效融合，形成一類復雜的組合優化問題——選址調度問題(ScheLoc)。

ScheLoc問題是近年來廣受關注的一類組合優化問題，最早由Hennes等[9]于2002年提出。ScheLoc問題有效融合了設施選址和機器調度兩類經典運籌優化問題，其決策環節主要包括設施的選址、設施和需求的分配以及各設施對所分配需求的服務次序等。按照設施數量，ScheLoc問題分為單機ScheLoc問題(即只有一個設施)[10-11]和并行機ScheLoc問題[12-13]；按照選址類型可分為平面ScheLoc問題(即在一定范圍內任意位置選址)[14]和離散ScheLoc問題(在指定待選位置集內選址)[15]。近年來，一些學者還就不確定環境下的ScheLoc問題進行了研究，形成了一些有意義的研究成果[16-17]。在現實生產生活中，ScheLoc問題被廣泛應用在港口管理[18]、礦石開采[19]、物流配送中心規劃[20]等問題的優化中。目前ScheLoc問題在軍事中的研究較少，Wesolkowski等[21]針對軍事訓練設施的選址和參訓部隊的訓練規劃進行了研究，以多種成本目標及總訓練時間的最小化為目標，構建了雙目標模型，并利用NSGA-Ⅱ算法進行了求解。值得注意的是，本文僅研究訓練設施選址和參訓部隊分配兩階段問題，未對各部隊訓練次序進行規劃。而本文所研究的預儲點選址與預置運輸配送組合優化，將預置運輸配送次序納入研究范圍，形成更完整的優化方案。

因此，本文針對裝備維修器材預儲預置問題，將預儲點選址和戰前裝備維修器材預置融合為ScheLoc組合優化問題，決策環節包括裝備維修器材預儲點的選擇、器材使用部隊(即需求點)與預儲點的分配關系，以及各預儲點進行器材預置時的保障次序，屬于離散并行機ScheLoc問題。通過考慮預儲點開設成本、運輸成本以及保障延誤懲罰成本等目標，構建混合整數規劃模型，并開發高效的求解算法，獲得全局最優的器材預儲預置方案，保證在作戰任務開始前快速完成裝備維修器材的部署，保障部隊作戰任務的開展。

1 問題描述

本文考慮在某戰略方向上，擬于適宜進行裝備維修器材預儲的待選位置集合中(通常選用現有裝備維修器材倉庫或其他已有設施場地)，選擇并設立若干預儲點進行裝備維修器材的預先儲存，并在戰爭開始前，按照部隊部署情況及時將器材預置至指定位置。具體過程可描述如下：

考慮某次實戰化演練中，保障部門擬在經勘查評估確定的l個備選位置中，最多選擇開發m個預儲點，記預儲點備選位置集合K={1,2,…,l}為預儲點備選位置集合，要在其中選擇開設m個預儲點。對位置k(k∈K)，其坐標為(Xk,Yk)，開設固定成本為ck，器材存儲上限為Qk，部署運輸車隊編組集合為Bk={1,2,…,b,…,|Bk|}，負責器材的運輸和預置。車隊編組b以整車隊形式獨立執行任務，不與其他編組進行車輛借調。假設本地域即將部署n個作戰部隊，構成部隊集合為J={1,2,…,n}，每個部隊j(j∈J)的坐標表示為(Xj,Yj)，根據作戰計劃，其對裝備維修器材的需求量為pj。在預置任務開始前，需要解決部隊器材需求和預儲點的分配，以及預儲點對各部隊預置器材的先后次序。當部隊j的需求分配至預儲點k時，由該預儲點的車隊b將器材從預儲點k運送至部隊j的部署位置，完成預置后立刻返回，執行下一次運送任務。假設每個車隊單次只運送一個部隊的器材，且該部隊的需求量能夠被車隊一次性保障完畢，其單程運送時間rjk和運輸成本ejk與部隊j與預儲點k之間的距離gjk有關，表示為rjk=gjk/s，ejk=egjk，其中s和e分別表示行車速度和單位距離運輸成本，本文均假設為定值。由于不同部隊擔負的任務不同，其對于器材需求的迫切程度也不同，假設部隊j的期望到達時間為dj。若在該期限內未能到達，將產生延誤時間，同時將影響部隊后續任務的開展，因此必須承擔一定的延誤懲罰成本。記Cj為部隊j的器材到達預定地域的時間，即保障完成時間，Tj為延誤時間，則Tj=max(Cj-dj,0)。定義qj為部隊j的單位時間延誤懲罰成本。本文的決策內容包括預儲點的選擇、部隊與預儲點的分配關系建立，以及預儲點運送器材的先后順序。為兼顧軍事效益與經濟效益，本文優化目標為預儲點總固定費用、總運輸成本以及總延誤懲罰成本的加權和最小，三者的權重分別表示為θ1、θ2、θ3。

2 模型構建

根據第1節的問題描述，為構造混合整數規劃模型，首先對問題進行如下假設：

1)預儲點固定開設成本可知；

2)戰時裝備維修器材采用基數化存儲，器材量單位為基數，且不區分器材品種；

3)戰時裝備維修器材采用集裝化運輸和機械化裝卸，其裝載、卸載時間忽略不計。

同時，定義如下決策變量：

wk=1，表示備選點k被選為預儲點，否則為0；

vjkb=1，表示部隊j由預儲點k的車隊b保障，否則為0；

xij=1，表示部隊j的保障次序在部隊i之后(無需相鄰)，否則為0。

由以上問題假設及變量定義，構建混合整數規劃模型，記為P，其表示方式如下：

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

Cj≥Ci+rik+rjk-L(3-xij-vjkb-vikb)

(7)

Ci≥Cj+rik+rjk-L(2+xij-vjkb-vikb)

(8)

Tj≥Cj-dj

(9)

Tj≥0

(10)

wk∈{0,1}

(11)

vjkb∈{0,1}

(12)

xij∈{0,1}

(13)

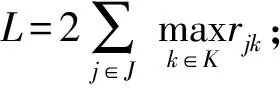
3 算法設計

本文問題是設施選址和并行機調度兩類問題的組合優化，設施選址和并行機調度問題已被證明均屬于NP-難問題[22-23]，因此本文研究的問題也屬于NP-難問題。組合優化使得問題能夠獲得全局最優解的同時，也極大地增加了模型的復雜度和求解難度，需要設計高效算法進行求解。針對該問題，本文首先生成一種基于邏輯的Benders分解(LBBD)算法，該算法是一種精確算法，在求解復雜的組合優化問題時性能較好。同時，為了對比組合優化與傳統優化方法的表現，還構造了一種序貫式優化(SH)算法。以下對兩種算法的原理和流程分別進行介紹。

3.1 基于邏輯的Benders分解

LBBD算法是一種基于松弛分解、迭代切割的精確算法。首先，經典Benders分解算法由Benders于1962年提出[24]，其基本原理為：將原問題中的復雜變量固定松弛，分解為一個主問題和一個子問題，主問題為原問題的松弛問題，其計算結果構成原問題的下界(LB)，主問題求解完成后將解傳至子問題，求解形成原問題的上界(UB)，子問題求解后生成Benders切割，并添加至下一迭代的主問題中，以提高問題下界。由此反復迭代，直至求得最優解(LB=UB)，或到達最大計算時限。經典Benders分解算法中，子問題形式被限定為線性規劃問題，限制了該算法的應用范圍。21世紀初，Hooker等[25]將經典Benders分解算法擴展，形成基于邏輯的Benders分解(LBBD)算法，其子問題可為任意優化問題。LBBD算法自提出以來，在組合優化問題的求解中展現出了顯著優勢，在機器調度[26]、路徑規劃[27]以及醫院手術室調度[28]等問題中得到了成功應用。

對模型P，首先將目標函數中保障延誤懲罰成本松弛，形成的主問題主要解決預儲點選址和部隊器材需求與預儲點的分配兩個決策問題，當以上決策變量求解并固定后，子問題則變為求解一系列單機調度問題，以在各車隊上最小化完成所有保障任務出現的延誤懲罰成本。隨后，子問題生成Benders切割，并添加至下一迭代中的主問題。值得注意的是，Benders切割可分為可行性切割和最優性切割，但在本文問題中，子問題求解時總存在可行解，因此本文所生成的Benders切割均為最優性切割。下面對主問題、子問題以及Benders切割的表示進行詳細描述。

3.1.1 主問題

為表示主問題，定義ψ為目標函數中總延誤懲罰成本的下界，將該部分以及對應的器材運送次序決策環節松弛，使得主問題成為研究預儲點選址、部隊與預儲點分配的松弛問題，松弛后的主問題表示為

(14)

s.t.

(2)式～(5)式，(11)式，(12)式，及

CUTS

(15)

此時，目標函數(14)式表示預儲點固定成本、運輸成本及總延誤懲罰成本下界的加權和。約束(15)式的CUTS即表示迭代過程中產生并添加至主問題的Benders切割。此時，由于對問題進行了松弛，ψ下界較差，使得主問題質量較差，需要根據問題結構特點提出有效不等式，對主問題進行加強。

3.1.2 有效不等式

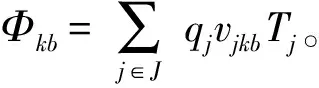
(16)

(17)

(18)

(19)

Φkb≥0

(20)

Tj≥0

(21)

(16)式表明總延誤懲罰成本不小于所有預儲點的車隊的延誤懲罰成本之和；(17)式表示總延誤懲罰成本不小于所有部隊各自延誤懲罰成本之和；(18)式表示各運輸車隊的延誤懲罰成本，不低于最小單位延誤時間懲罰成本與最小延誤時間的乘積，其中，最小延誤時間以車隊保障最后一個部隊的最短用時與最大期望到達時間之間的差；(19)式表示部隊j的延誤時間不小于該部隊與所所分配的預置點之間的距離與期望到達時間的差，即部隊j為車隊的第一個保障對象。

3.1.3 子問題

當主問題求解完畢后，預儲點選址變量wk、分配變量vjkb等的值得以確定，此時子問題則變為求解一系列單機調度問題，即在各預儲點位置上被分配有器材預置任務的車隊，其保障次序的確定，目標為最小化該車隊產生的總保障延誤懲罰成本。定義集合Jkb為預儲點k中車隊b所承擔的部隊器材預置任務，即Jkb={j|vjkb=1,?j∈J}。定義變量zij表示部隊i和j的保障次序相鄰，且i在j之前。則對預儲點k中車隊b的子問題可表示為

(22)

s.t.

zij+zji≤1

(23)

Cj≥Ci+rik+rjk-L(1-zij)

(24)

Cj≥rjk

(25)

Tj≥Cj-dj

(26)

Tj≥0

(27)

zij∈{0,1}

(28)

目標函數(22)式表示在預儲點k中車隊b處的總延誤懲罰成本最小化；約束(23)式表示兩部隊i和j的保障次序關系，即部隊i不可能同時既是部隊j的前一保障對象又是部隊j的后一保障對象；約束(24)式～(27)式與對應前述約束(7)式～(10)式；約束(28)式為變量zij的域。

根據Graham等[29]提出的三段分類法，此處所描述的子問題可表示為1‖∑qjTj。該問題已經被證明為強NP難問題。當前對1‖∑qjTj問題的求解已有較多文獻，其中精確算法包括分支定界、動態規劃、列生成等。經過前期試驗，由Tanaka等[30]提出的基于動態規劃的精確方法具有良好的性能。該方法基于提出的Ibaraki等[31]提出的SSPD算法，通過多種改進策略，解決了SSPD算法內存使用大、計算效率低等問題，經過數值實驗，這種基于動態規劃的方法能夠在合理時間內求解工件數量(即本文中的部隊數)達300的無空閑時間的單機調度加權延誤時間最小化問題。因此，本文應用Tanaka等的動態規劃方法對子問題進行求解，并基于子問題的結果生成Benders切割。

3.1.4 Benders切割

(29)

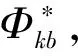
3.2 傳統序貫式算法

為比較組合優化方法與傳統優化方法的性能，本節構造一種序貫式優化方法(記作SH)，通過兩個階段依次對問題進行求解，即：先以預儲點開設固定成本和運輸成本最小化為目標，求解預儲點選址和部隊需求分配問題。第一階段完成后，第二階段轉化為針對承擔預置任務的各運輸車隊單機調度問題，優化目標為總延誤懲罰成本最小化。為了保證算法的性能，兩階段分別使用精確方法進行求解。下面分別對各階段的求解方法進行詳細描述。

3.2.1 第一階段

本階段以預儲點固定成本和運輸成本最小化為目標，構造MILP模型如下：

(30)

s.t.

(2)式～(5)式，(11)式，(12)式

3.2.2 第二階段

第一階段求解完成后，選址變量wk和分配變量vjkb得以固定，此時第二階段轉化為一系列求最小延誤懲罰成本的單機調度問題。該問題與3.1.3節類似，為提高后期數值實驗計算結果對比的可信度，本階段采用與4.3節相同的求解方法，即Tanaka等[30]的基于動態規劃的精確求解方法。

4 數值實驗

為評估本文所提出的模型和算法的性能，隨機生成160個算例對模型P及算法LBBD和SH進行測試實驗，首先對算例的生成規則進行簡要介紹，隨后對實驗結果進行匯總和分析。

4.1 算例生成

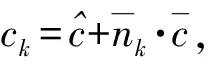
本文所提出的模型P、算法LBBD和SH，均通過C++鏈接求解器Cplex12.10編程實現，其中模型P利用CPLEX求解器直接求解時，其內核算法為分支切割算法。每個算例的求解時限設置為600 s。運行環境為Intel Xeon CPU E5-2690 v3，2.60 GHz，32 GB RAM。為更好地對計算結果進行分析，將該部分算例分為3組，分別是常規算例組(20≤n≤60)、大算例組(80≤n≤120)和超大算例組(140≤n≤200)。下面分別對各組算例的計算結果進行分析。

4.2 常規算例組結果

常規算例組的計算結果如表1所示，表格中前4列表示算例相關參數，分別為部隊數n，待選位置數l，預儲點數m，以及各預置點運輸車隊數b。中間3列表示各模型和算法的求解質量，用上界UB和下界LB的差值百分比Gap(%)度量，其計算方式可表示為

(31)

值得注意的是，SH是一種兩階段序貫式優化方法，無法準確獲得整個問題的有效下界，因此其下界采用模型P和算法LBBD所生成的最好下界，并利用其自身上界求得算法SH的Gap值。由于本節所生成的算例考慮TF和R值不同，每種規模的算例共有4個具有不同期望到達時間的算例，因此表1中各算例數值為4個算例的平均值。最后一行括號內數字代表該組取得最優解(Gap=0)的算例的數量。表格右側3列為各算例的計算時間。

從表1中可以看出，在常規算例組的實驗中，本文所提出的模型P和算法LBBD均取得了良好的求解效果，LBBD算法獲得了最多得最優解，為28個，模型P得到27個最優解，略低于LBBD，而算法SH僅有2個最優解。LBBD算法的平均Gap值為3.10%，在三者中表現最好，模型P的Gap值為3.71%，高于LBBD算法，但明顯好于SH算法的25.69%。從求解效率上看，LBBD同樣表現最好，其平均計算時間為262.77 s，模型P的平均計算時間為279.99 s。SH由于采用序貫式優化方法，其問題復雜度低，平均求解時間不到1 s，但同時解的質量較差。

從表1中還可以觀察到，對模型P和算法LBBD，總體上看，其運輸車隊數量越多，解的質量越好。從表1中可以統計發現：在該組算例中，當車隊數量為3時，模型P平均Gap為4.53%，算法LBBD的平均Gap值為3.71%；當車隊數量為5時，二者分別降為2.95%和2.49%，降幅均超過30%。其可能的原因為：在同等算例規模下，當車隊數量較少時，每個車隊將分配更多需求，由于以加權延誤時間最小化為目標的單機調度問題為NP難問題，其求解復雜度高，可能造成求解質量相對較低。

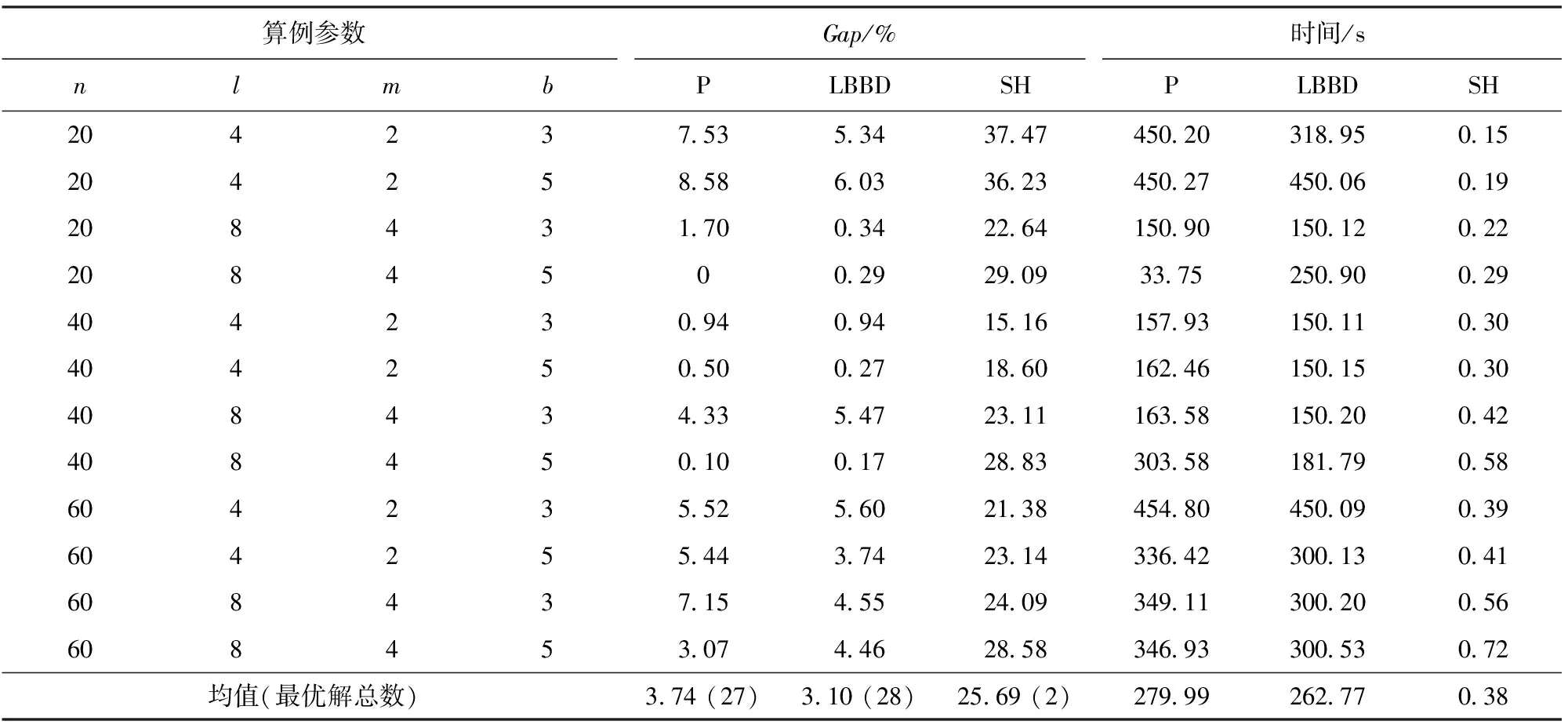
表1 常規算例組計算結果

4.3 大算例組結果

大算例組為部隊數量為80～120的算例，計算結果如表2所示。從表2中可以看出，大算例組的求解難度相對于常規算例組有所增大，模型P的表現出現明顯下降。從求解質量上看，模型P共取得15個最優解，其平均Gap值為19.78%，平均用時為493.27 s。LBBD算法得到27個最優解，其平均Gap為5.32%，平均計算時間為263.04 s，明顯優于模型P。SH的計算效率仍最高，平均計算時間在 1 s 以內，但其求解質量相對較差，其平均Gap高達21.11%，共獲得12個最優解。

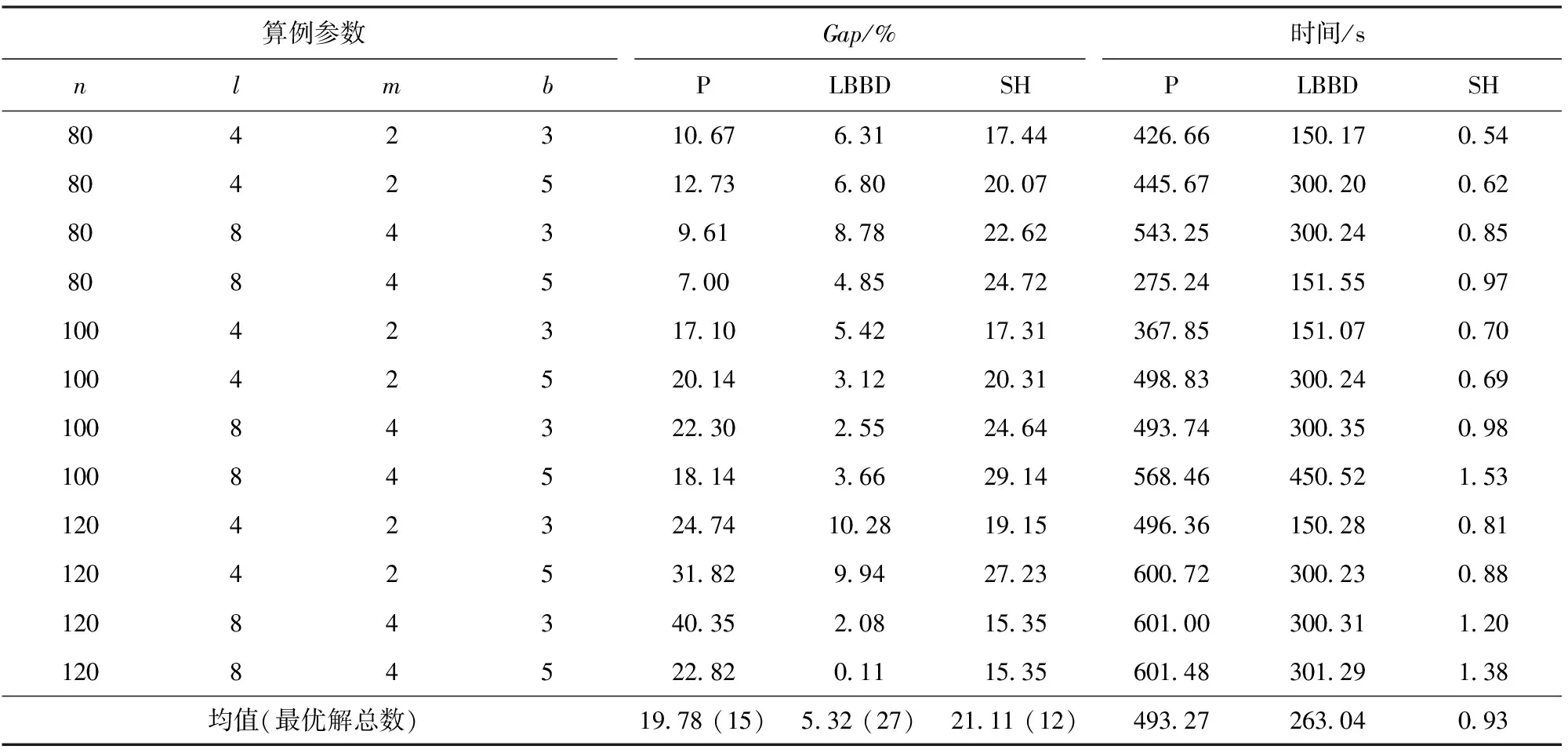
表2 大算例組計算結果

4.4 超大算例組結果

為進一步評價和探索模型P及算法LBBD、SH的性能，本文對超大規模算例進行了實驗，該組64個算例中，部隊數n={140,160,…,200}。即：決策者要對某戰略方向上最高達200個裝備維修器材預置任務進行預儲點選擇和預置方案決策，計算結果如表3所示。

針對表3中的計算結果，從求解質量上看，算法LBBD的表現相比模型P和算法SH具有明顯優勢。在64個算例中，LBBD共求得34個最優解，其平均Gap值為8.00%。SH獲得18個最優解，其平均Gap值為23.11%。模型P隨著算例規模的增加，表現顯著下降，在超大規模算例中性能最差，僅在n=140的算例中獲得2個最優解，平均Gap值達到80.21%，遠高于算法LBBD和SH。在n=180的算例中，模型P的平均Gap值均在85%以上，而當n=200時，平均Gap值均大于98%，此時模型P已基本失去優化求解能力。從計算時間上看，模型P平均計算時間為596.39 s，接近計算時限600 s，算法LBBD的平均計算時間為289.83 s，相比表2中的263.04 s較穩定，算法SH的平均計算時間只有1.4 s。

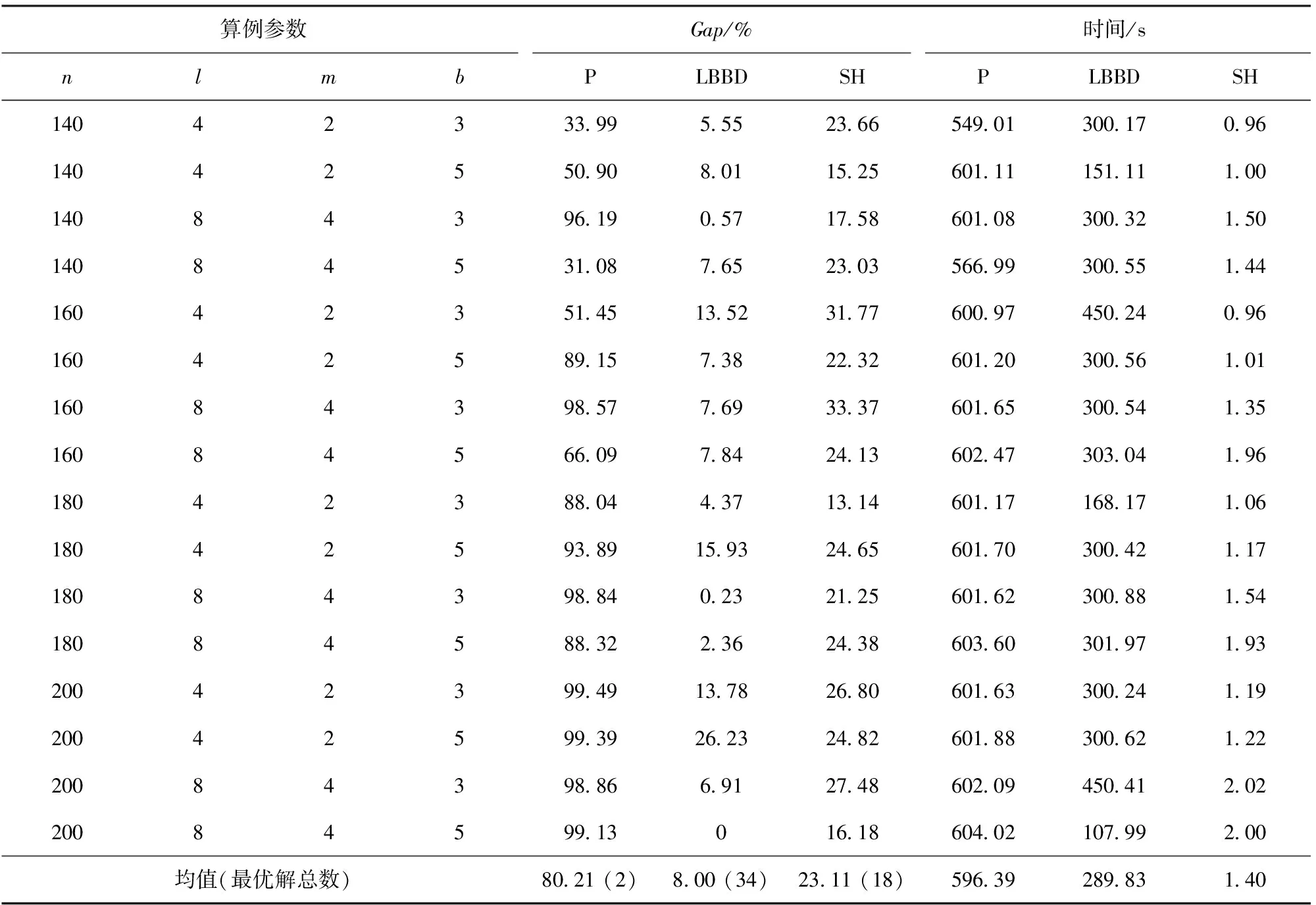
表3 超大算例組計算結果

從3組算例的計算結果來看，算法LBBD在3種方法中表現最好。在160個算例中，LBBD共求得89個最優解，總平均Gap值為5.73%；算法SH獲得32個最優解，其平均Gap值為23.29%；模型P獲得44個最優解，平均Gap值為39.14%。當算例規模增大時，模型P的性能下降明顯，在48個常規算例中，模型P求得27個最優解，平均Gap值為3.74%，而在64個超大算例中，兩項數據分別變為2個和80.21%，說明在本文所研究的組合優化問題具有較高的復雜性。而算法LBBD保持了良好的求解穩定性，3組算例的平均Gap值分別為3.10%，5.32%和8.00%。在組合優化LBBD算法與序貫式優化方法SH算法的比較中，LBBD的求解質量顯著高于SH，證明了組合優化方法在獲得更高質量解方面的優勢。

同時，分析表1～表3的結果發現，算法SH求得的最優解數量隨著算例規模的增大而增加，經過分析發現，其原因主要與期望到達時間有關。因此，接下來對不同期望達到時間對問題求解的影響進行分析。

4.5 期望到達時間的影響

4.1節詳細介紹了期望到達時間的生成方法，其中參數TF的大小影響整體的松緊程度，即TF值越大，整體期望達到時間越短，表明戰爭的突發性越強，需要在最短時間內完成器材預置；反之，整體期望達到時間越長，體現戰爭準備時間較充裕。參數R的值反映了不同部隊對器材到達時間需求的差異性。R值越小，說明期望到達時間分布越集中，反之則越分散。本節對不同TF和R值組合下各模型和算法的表現進行分析，其結果如表4所示。值得注意的是，表4中每個結果均為40個算例結果的平均值，括號內為取得的最優解數量。

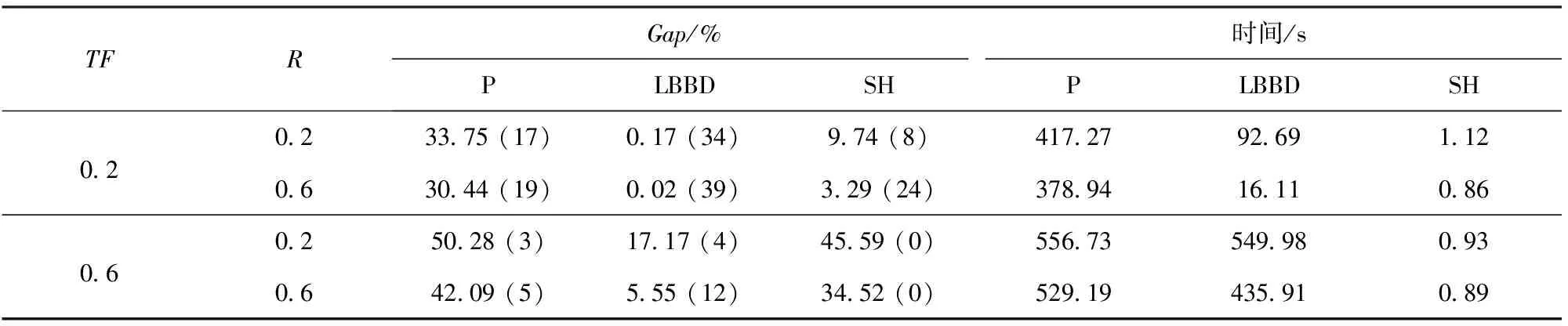
表4 期望到達時間的影響

從表4的結果來看，不同TF和R值的組合對各模型和算法的求解具有顯著影響。當(TF,R)=(0.2,0.6)時，表明整體期望到達時間較長，且分布較散，即：戰爭準備時間充足，各部隊需求緊迫性差異大，此時問題復雜度較低，因此各模型和算法表現較好。以算法LBBD為例，在該組的40個算例中，LBBD取得39個最優解，平均Gap僅為0.02%，平均計算時間16.11 s，明顯好于在其他(TF,R)組合中的表現。在該組中，算法SH獲得24個最優解。由于當算例規模增大時，運輸成本在目標函數中的比重上升，而該組延誤懲罰成本較低，使得SH獲得最優解的能力上升。因此，在表1～表3中，算例規模越大，算法SH獲得的最優解數量越多。當(TF,R)=(0.6,0.2)時，表明戰爭準備時間較短，且各部隊均面臨緊迫的裝備維修器材需求，此時問題求解難度最大。在各模型和算法中，LBBD算法表現最好，其平均Gap值為17.17%，明顯好于模型P的50.28%及算法SH的45.59%。

從動態角度看，當TF值不變，R值由0.2增加至0.6時，表示各部隊期望到達時間由集中變得分散，此時各模型和算法獲得的最優解數量增加，平均Gap值降低，平均計算時間縮短。以算法LBBD為例，TF=0.2情況下，當R值由0.2變為0.6時，平均Gap值由0.17%降為0.02%，最優解數量由34變為39，平均計算時間由92.69 s縮短為16.11 s。當R值不變、TF值增大時，表示整體期望到達時間縮短，從表4的數據來看，問題求解難度大大增加，各模型和算法的表現均有下降。以模型P為例，R=0.2情況下，當TF值由0.2變為0.6時，平均Gap值由33.75%增至50.28%，最優解數量由17變為3，平均計算時間由417.27 s變為556.73 s。同時，從表4中結果可以總結發現，TF值變化所產生的影響遠大于R值變化的影響，即：戰爭準備時間是否充足，是影響裝備維修器材預儲預置決策難度的主要因素。同時，決策者也應關注不同部隊需求緊迫性之間的差異。

5 結論

本文研究了裝備維修器材預儲點選址與預置運輸及配送優化方法，將預儲點選址與戰前器材預置融合為一類選址調度組合優化問題，構建以預儲點固定成本、運輸成本與保障延誤懲罰成本最小化為目標的混合整數線性規劃模型，設計了一種基于邏輯的Benders分解算法(LBBD)和一種序貫式優化方法SH，并基于160個隨機算例進行了數值實驗。得出以下主要結論：

1)該問題屬于NP難問題，對模型P直接求解時，其表現隨問題規模增加而顯著下降，需要開發高效的求解算法。

2)提出的LBBD算法獲得的最優解數量最多，求解質量最好。序貫式算法SH采用兩階段分別精確求解的優化方法，其求解效率高，但求解質量低。LBBD與SH算法的對比實驗證明組合優化方法在獲得更高質量解方面具有優越性。

3)戰爭準備時間以及不同部隊期望到達時間的差異性對問題的求解具有重要影響，進一步表明了裝備維修器材預儲預置的總要性。

下一步可針對考慮戰時不確定性和中斷風險的裝備維修器材供應保障優化方法進行研究。