診斷思維痛點 避免易錯堵點
——剖析解三角形綜合問題時的思維痛點

浙江 余繼光

數學基礎教育研究中最重要分支是解題思維，而數學解題思維中最重要的兩個方面內容，一是數學解題思維痛點(漏點、錯點、智慧點缺失等，本質上就是易錯點)剖析研究；二是數學解題經驗積累，包括教學經驗與學習經驗，研究的方法就是思維剖析(最有效最真實的是答題情況分析)、案例研究、統計分析、大數據研究.

解三角形一般被認為是較容易的一類題，然而面對較復雜的求解三角形的綜合問題，許多學生無法越過眾多數學思維障礙，導致求解失敗.分析失敗的成因，在已知三大定理與一大公式(內角和定理、正弦定理、余弦定理和三角形面積公式)的基礎上，如何識別數學情境中隱藏的代數或三角結構成為關鍵，只有在數學思想的引領下，經過熟練的三角變換或運算將三定理與一公式有機串起來，鏈接能力才能形成.

1 運算不熟練不到位之痛

解三角形的綜合問題離不開代數與三角運算，比如，遇到高次函數時的換元降次，遇到無理函數時，借助于三角代換轉化為有理函數等.

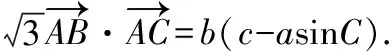
(Ⅰ)求角A的大小；

(Ⅱ)設b=c，N是△ABC所在平面上一點，且與點A分別位于直線BC的兩側，如圖，若BN=4，CN=2，求四邊形ABNC面積的最大值.

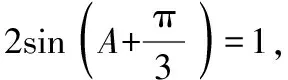
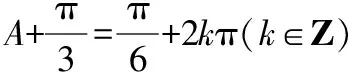
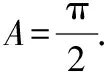
又a2=2b2，

四邊形ABNC的面積

令t=8cosθ(0<θ<π)，

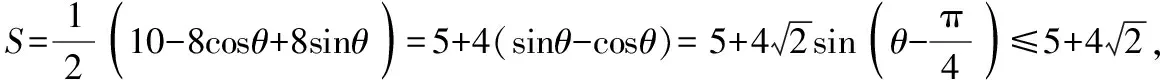
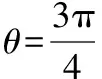
易錯點：面積函數中遇到高次表達式、無理函數時，缺少降次意識與無理轉化為有理的技術.

痛點分析：

(1)第(Ⅰ)問，邊角之間的靈活轉化是求角A的關鍵，合一變換以及解三角方程是基本功；

(2)第(Ⅱ)問，如何選擇變量建立面積函數是一個智慧點，根據題設給定的邊的關系以及對角A的確定，從而找到a2=2b2是一個關鍵點；

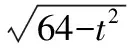
(5)最后借助于合一變換，化簡函數，利用正弦函數有界性求出函數最大值.

2 三角變換不熟練之痛

幾何問題中的代數問題，比如求最值，需要建立目標函數，涉及選擇參變量，建立數學模型，而復雜的三角模型需要通過三角變換轉化為標準的三角函數，此過程的基本功就是三角變換力.

【問題2】(2019·稽陽聯考改編)等腰直角△ABC中，AB=AC=1，在AB,AC上分別取D,E，沿DE折疊，A恰好落在邊BC上，則AD的最小值為________.

解析：A在BC上投影為P，

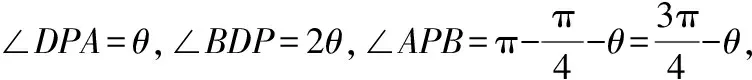
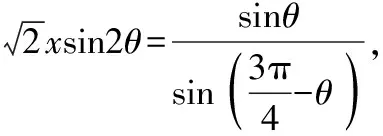
易錯點：在復雜三角形中缺少引參技術，建模技術，平面幾何與三角函數的基礎掌握不牢.

痛點分析：

(1)一是審題能力不足——不能理解題意把握問題本質：幾何信息代數化、三角化，為建立函數模型打下基礎；

(2)二是方法不得當——不能將幾何條件轉化到三角形式，不會選擇一個角與目標量建立關系，不能迅速建立目標函數來解決給定的問題；

(3)引入角建立目標函數是一個痛點，分析三角形內各角之間的聯系也是一個痛點；

(4)通過兩個三角形內運用正弦定理，找橋、用橋、然后拆橋(BP)，建立AD的目標函數——數學模型，利用三角函數有界性確定函數最值.

3 隱藏條件挖掘不到位之痛

看似簡單的代數條件可能隱藏著關鍵的幾何關系，通常的字母到數的思維可能轉變為由數到字母的變形，從而找到問題的結構.

【問題3】(2020·天利圖書聯考改編)已知a,b,c分別為△ABC的內角A,B,C的對邊，若a=4，c2=2b2-32，則△ABC面積的最大值為________.

解法1：(建立面積函數，進而求函數的最大值)

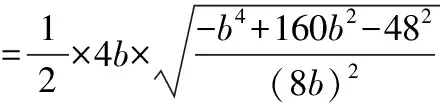
從而可知，當b2=80時，△ABC面積最大，最大值為16.

解法2：(利用余弦定理邊角互化)c2=2b2-2a2.

又b2=c2+a2-2accosB,

兩式聯立可得c2=2c2-16ccosB，c=16cosB，

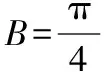
解法3：(挖掘直角三角形的性質)

如圖，過C作AB的垂線交AB于點D，

在兩個含高CD的直角三角形中，

令BD=x，則AD=c-x，設CD=h,

所以b2=(c-x)2+h2，a2=x2+h2,

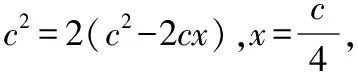
從而可得ch≤32，則△ABC面積最大值為16.

易錯點：建立面積函數遇到高次和無理函數時，缺少對結構的把握，三角形的邊角轉化技術不牢.

痛點分析：

(1)解法1中挖掘余弦定理與三角形面積公式間的關系，不了解則產生障礙與痛點；

(2)解法2中挖掘余弦定理結構特征與三角函數有界性關系，智慧點達不到產生痛點；

(3)解法3中挖掘直角三角形中邊角關系，挖掘不到位產生痛點.

4 題設條件挖掘不到位之痛

三角形中3條邊3個角不是獨立的變量，受到“三定理一公式”的制約，還受到三角函數的制約，尋找到它們之間的聯系才能突破問題的障礙.

化簡得a2+h2-mn=3ah，c2=m2+h2,b2=n2+h2,

則a2+b2+c2=2h2+m2+n2+a2=2a2+2h2-2mn=6ah=24.

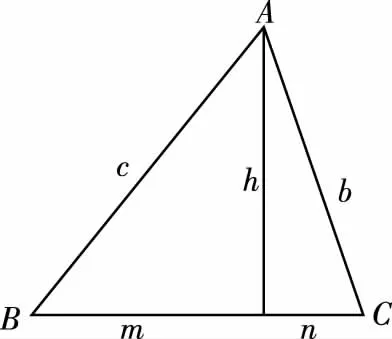
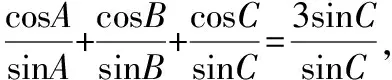
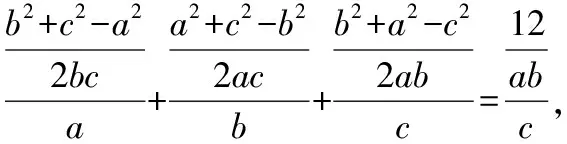
整理得a2+b2+c2=24.

易錯點：三角形中邊角之間的聯系信息挖掘不到位，鏈接不到位，轉化不到位.

痛點分析：

(1)解法1中利用三角函數定義將角的關系轉化為邊的關系，挖掘不到位產生痛點；

(2)解法2中將正切函數轉化為正余弦函數，然后利用正弦與余弦定理轉化到邊的關系，挖掘不到位產生痛點.

5 缺少“邊角統一思想”之痛

解斜三角形問題時，對于邊角之間的數量關系，需要通過“三定理一公式”將其統一起來，發現內在聯系與結構，缺少“統一”思想，處處遇到障礙.

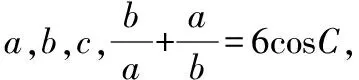
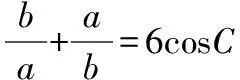
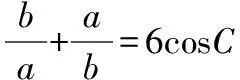
6cosCsinAsinB=sin2A+sin2B.

由余弦定理c2=a2+b2-2abcosC，

結合正弦定理c=2RsinC，b=2RsinB，a=2RsinA，

代入得sin2C=sin2B+sin2A-2sinBsinAcosC

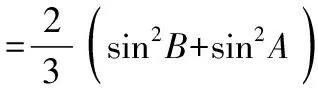
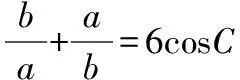
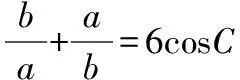
當A=B或a=b時滿足題意，

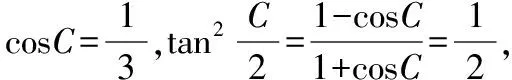
易錯點：主干條件轉化缺少統一到邊、統一到角的思想，目標結論三角變換公式不到位.

痛點分析：

(1)解法1在統一到角的思想支配下進行推理，缺少者產生痛點；

(2)解法2在統一到邊的思想支配下進行推理，缺少者產生痛點；

(3)對輪換結構思想不了解，不會想到解法3.

6 缺少多角度審視三角形之痛

高考數學中的解三角形問題，題設條件是命題專家精心設計的“局”，學會多角度審視其中的條件結構，深入的挖掘隱藏的內容，一般都可以突破.

解法1：(解三角形法)

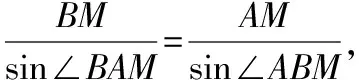
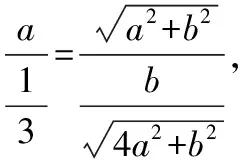
解讀：通過分析給定三角形的特征，由△ABM中的邊角數量關系過渡到△ABC中邊角數量關系，在△ABM中(斜三角形)利用正弦定理，在△ABC中(直角三角形)利用三角函數定義，運算思路清晰，運算的關鍵點是尋找AC與BC的大小關系.

解法2：(三角函數定義法)以A為坐標原點，AB所在直線為x軸，建立如圖直角坐標系，

所以8c2=(a+b)2①.

又由勾股定理知b2=a2+c2+(b-a)2+c2②，

解讀：利用三角函數定義，將∠CAB與∠BAM的AB邊為始邊，把研究這兩個角的正弦值轉化為研究點M，C的坐標之間關系，回歸三角函數定義是多么地令人鼓舞！

解法3：(三角形面積法)AC=b,BC=a,S△ABC=2S△ABM，

解讀：從上述兩解法中可以看出，尋找AC與BC的大小關系是問題的突破口.而解決這一突破的方法還有許多，比如利用三角形面積S△ABC=2S△ABM，以及直角三角形的勾股定理！

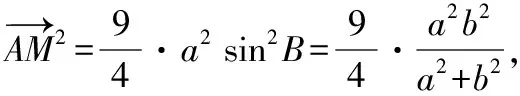
解讀：類似于三角形面積法一樣，尋找AC與BC的大小關系是問題的突破口.借助于向量運算及正弦定理也能解決這一障礙.

解法5:(三角變換法)設BM=MC=1，AC=x，

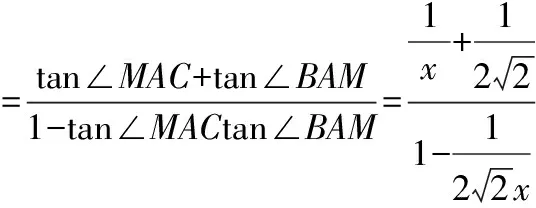
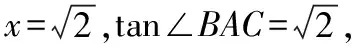
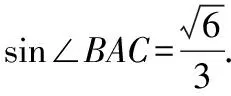
解讀：三個角∠CAB，∠BAM，∠CAM之間的關系：∠CAB=∠BAM+∠CAM，很容易聯想到兩角和的三角函數正切公式，把這一公式與三角函數定義溝通，就可突破！

易錯點：在復雜三角形中，尋找“橋”變量的意識不到位，不會在不同三角形中搭橋鋪路.

痛點分析：

(1)解法1突出分析三角形中的邊角關系；

(2)解法2突出利用三角函數定義將三角函數與點的坐標緊密聯系；

(3)解法3巧妙利用三角形面積關系尋找到邊與邊間的數量關系；

(4)解法4巧妙利用向量工具尋找到邊與邊間的數量關系；

(5)解法5突出利用三角變換工具求出目標函數的值.

7 缺少三角運算力之痛

三角函數有其固有的規律，角的規律與邊的規律不同，前者借助于三角變換與運算，后者借助于代數變換與運算，兩者之間靈活地轉化與串聯是智慧，缺少就是易錯點，就是痛點.

(Ⅱ)若BC=17，CA=6，求AB;

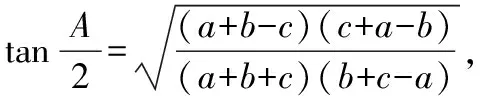
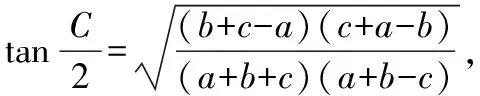
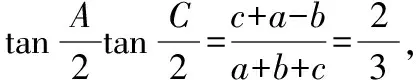
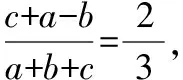
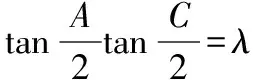
(1-λ)2(1-cosA)(1-cosC)=2λ2(1-cosB),

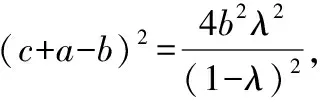
易錯點：對已知信息中正切函數與余弦函數間的聯系，鏈接余弦定理的意識不到位.

痛點分析：

(1)問題(Ⅰ)中半角的正切與余弦定理間的聯系推不出而產生思維痛點；

(2)問題(Ⅲ)中代數式的推演能力達不到而產生痛點.