見山非山 舉一反三
——以2022年全國新高考I卷第21題為例
廣東 黃林盛
《中國高考評價體系》指出,綜合性要強調融會貫通.直線與圓錐曲線的問題具有很強的綜合性,考查的落腳在定點、動點、定直線、動直線與曲線的位置關系.在考查“四基”與“四能”的同時體現核心素養立意,引導師生在經歷解決問題的過程中探究問題背景知識的發生與發展過程,以達到掌握問題的本質.本文對2022年全國新高考Ⅰ卷第21題進行多角度剖析、一題多解,為圓錐曲線的教學提出幾點思考,與同行交流.
1.真題呈現,妙法迭出
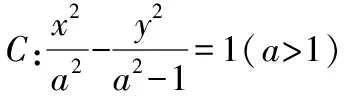
(1)求l的斜率;
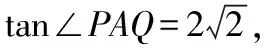
1.1 試題分析
本題文字敘述簡潔明了,設問方式平易近人,第(1)問與以往不同,不是簡單的求曲線方程,容易給考生帶來一定心理壓力.本題從知識層面看,主要考查雙曲線的標準方程、直線與雙曲線的位置關系以及張角模型中三角形面積問題.試題的重點是將題設中的幾何條件進行代數化,難點是選擇恰當的方法優化運算;從能力層面上看,突出考查考生數形結合思想和邏輯思維能力、運算求解能力以及綜合運用所學知識分析問題和解決問題的能力,是學科素養中“研究探索”方面的要求.
1.2 解法剖析
剖析一:問“道”于題,循“敘”漸進
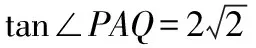
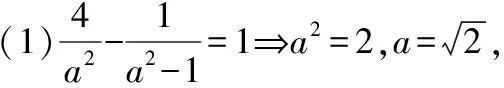
設直線l的方程為y=kx+m,P(x1,y1),Q(x2,y2),由題知A(2,1),
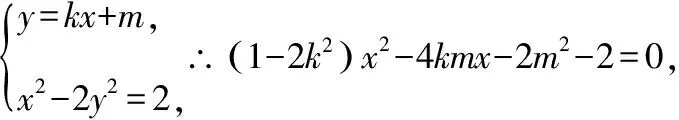
∴2kx1x2+(m-1-2k)(x1+x2)-4(m-1)=0,
∴2k2+k-1+km+m=0,(k+1)(2k-1+m)=0,
當2k-1+m=0時,m=1-2k,
直線l方程為y=kx+1-2k=k(x-2)+1,恒過定點A(2,1)不可能,舍去.
∴k=-1.
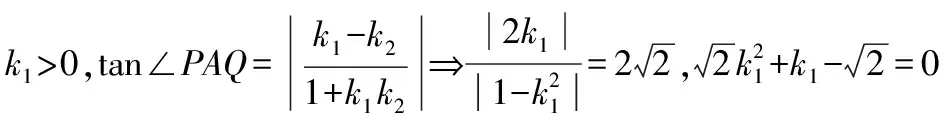
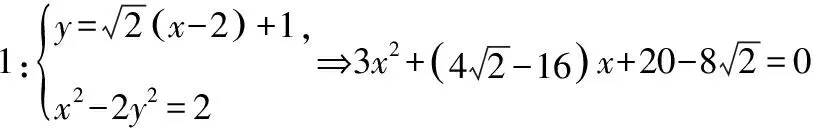
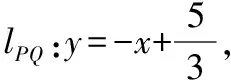
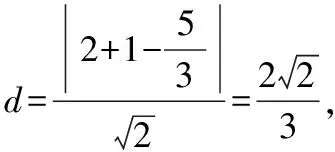
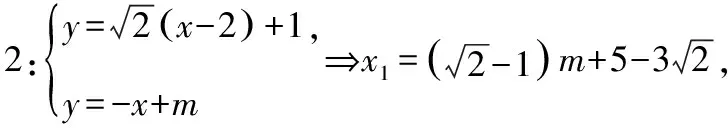
以下同算法1.
評注:此解法是通法,遵循題目的表述,翻譯成數學符號,逢相交便聯立,遇交點求坐標,是圓錐曲線綜合問題的常規求解思路,但未經等價轉化的運算比較繁雜.
剖析二:活用“算”理,統籌全局
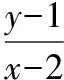
解法二:(齊次化)設PQ:m(x-2)+n(y-1)=1,

(x-2)2-2(y-1)2+4(x-2)-4(y-1)=0,
聯立(齊次化)可得
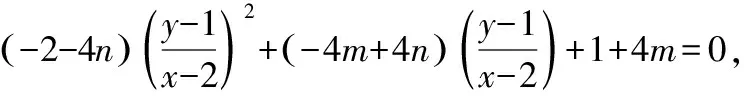
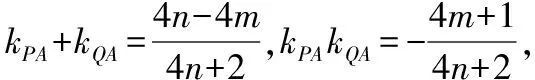
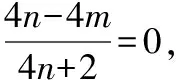
即PQ:m(x+y-3)=1,
故kPQ=-1,在第(2)中易得kPAkQA=-2,
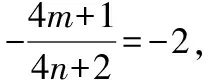
則lPQ:3x+3y-5=0,以下同解法一.
評注:抓住題目條件與特征,結合兩直線斜率和為零的條件,求解另一直線的斜率為定值.充分厘清題目的背景與題意,同時又要跳出“題面”,進行全局審視,通過構造關于斜率的一元二次方程,借助整體思維,從而得到這個關鍵代數式,達到轉化求解的目的.
剖析三:轉換視角,從“曲”到“直”
對于斜率最容易想到的就是利用斜率公式來進行表示,在圓錐曲線中,如果要表示某條弦所在直線的斜率,常用兩種方法:利用斜率公式和利用點差法.
本題可以運用點差法將點在雙曲線上轉化到直線上,從而同構出直線方程,以達到減少運算量的目的.
解法三:(同構直線)算法1(點差法):


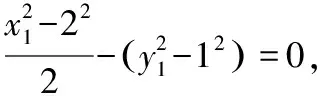
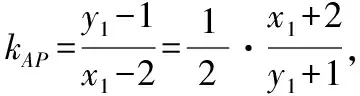
由題意可得kAP+kAQ=0,
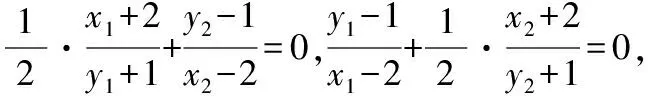
化簡有2y1y2+2(y2-y1)+x1x2+2(x2-x1)-6=0④,
2y1y2+2(y1-y2)+x1x2+2(x1-x2)-6=0⑤,
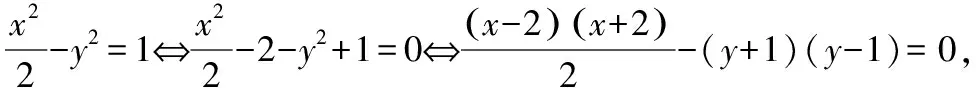

將P(x1,y1),Q(x2,y2)代入上式有
以下同算法1.
評注:通過點差法將點在雙曲線上轉換到直線上,體現整體思想.對運算法則、運算思路、選擇運算方法有較高的要求.有些學生對圓錐曲線上的兩個動點運用點差法很熟練,但是當其中一個點換成定點之后就想不到用點差法了,這是對點差法理解不夠深刻的原因.設點過程中若不能“減元設點”,意味著參與運算的變量過多,進而導致“趨同組合”的方式靈活多變,操作難度加大,不過若“趨同組合”成功,解題便柳暗花明變得異常簡單,所以設點法的運算具有“多想少算”的特點.
2 真題互鑒,題源追溯
2.1 真題互鑒

(1)求C的方程;
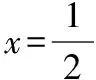

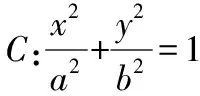
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為-1,證明:l過定點.
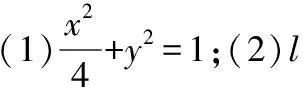
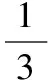
(1)證明:△PAB的內切圓的圓心在一條定直線上;
(2)若∠APB=60°,求△PAB的面積.
從真題1、真題2、真題3以及2022年全國新高考Ⅰ卷第21題來看,考查一致的核心知識點是直線與圓錐曲線的位置關系、兩直線斜率之和為定值的問題.2022年全國新高考Ⅰ卷第21題第(1)問是2021年全國新高考Ⅰ卷四點共圓的退化情形,是真題2的特殊,與真題3更是如出一轍.本文從基本解法到巧妙解法的呈現遵循了“拾級而上”的思維升華,體現了豐富的數學思想方法.通過對思想方法進行深度挖掘,探究其本質,掌握其規律,以達到運用數學的思想方法促使數學試題“成群生長”的目的.
2.2 題源追溯
通過對試題的剖析和多種解法及與三道歷年真題互鑒,發現2022年全國新高考Ⅰ卷第21題第(1)問是一類兩直線斜率的和為定值,使得直線斜率為定值(或定點)的問題.下面進行題源追溯,可得到更多一般結論.
結論1(普通高中課程標準實驗教科書人教A版數學選修4-4坐標系與參數方程第38頁例4引申)已知AB,CD是中心為點O的橢圓的兩條相交弦,交點為P,兩弦AB,CD與橢圓長軸的夾角分別為∠1,∠2,且∠1=∠2,則|PA|·|PB|=|PC|·|PD|.
結論2(2022年全國新高考Ⅰ卷第21題出題背景)當點P(x0,y0)(y0≠0)在曲線上時,過點P作兩條斜率互為相反數的直線,與曲線的另外兩個交點分別為A,C,則直線AC的斜率為定值.


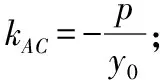
證明過程略.
將結論2的兩直線斜率和與積的定值一般化,可得到結論2的推廣.
推廣:設P(x0,y0)是曲線λx2+μy2=1(λμ≠0)上的一個定點,PA,PB是該曲線的兩條弦,其所在直線的斜率分別為k1,k2.則
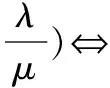
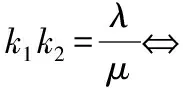
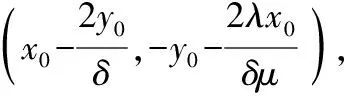
k1+k2=0?直線AB的方向向量為(μy0,λx0).
通過對試題第⑵問剖析真題3進行互鑒,可以發現這是圓錐曲線張角模型中三角形面積問題,可得到一般結論.
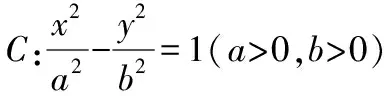
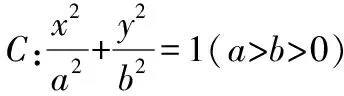
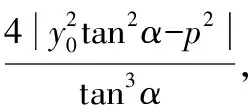
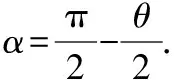
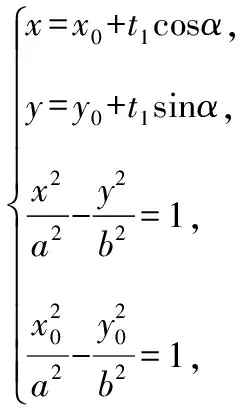
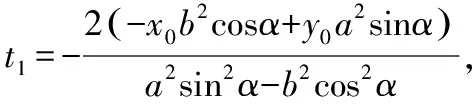
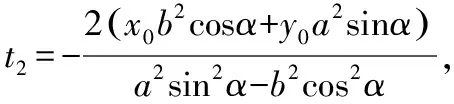
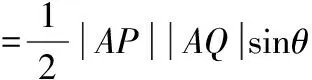
運用結論3.1解答2022年全國新高考Ⅰ卷第21題第(2)問如下: