一道高考解析幾何題的思考與探索

常梨君 金一鳴

(江蘇省常州市田家炳高級中學(xué),213000)

解析幾何在高中數(shù)學(xué)學(xué)習(xí)中占有舉足輕重的地位,近幾年高考對直線與圓錐曲線相交問題的考查更是主流.這類問題的常見解題思路為:將條件和結(jié)論坐標(biāo)化,聯(lián)立直線與圓錐曲線方程,利用韋達(dá)定理解決問題.解析幾何問題的解題思路是清晰的,但多元變量運(yùn)算的繁、難是導(dǎo)致學(xué)生“畏算”的主要因素.若解題方法選取得當(dāng),則會(huì)將大大降低運(yùn)算難度,實(shí)現(xiàn)“巧算”.本文以2022年新高考I卷第21題第(1)問為載體,探討解析幾何問題解決的常見解題策略(此題的背景和方法也可推廣到橢圓和拋物線).

一、試題呈現(xiàn)

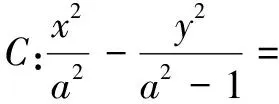
(1)求l的斜率;

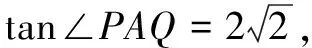
二、解法賞析

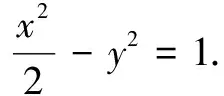
1.常見解法

解法1(設(shè)而不求)

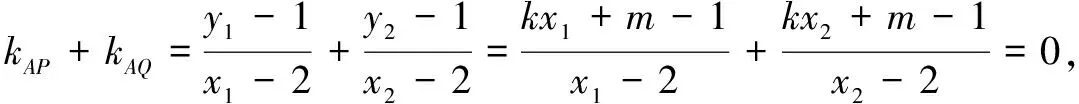
2kx1x2+(m-2k-1)(x1+x2)-4(m-1)=0.

①

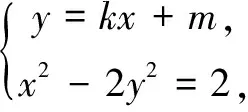
當(dāng)m=1-2k時(shí),直線PQ的方程為y=kx+1-2k,過定點(diǎn)A(2,1),不合題意,舍去.所以k=-1.

評注從結(jié)論出發(fā),設(shè)出目標(biāo)直線PQ的方程(含雙參k,m),借助條件kAP+kAQ=0構(gòu)建k和m的方程,找出k和m的等量關(guān)系,得到定值,這是通性通法,易想但運(yùn)算量不小.

解法2(設(shè)而求之)

設(shè)直線AP，AQ的斜率分別為k1,k2,點(diǎn)P(x1,y1),Q(x2,y2).

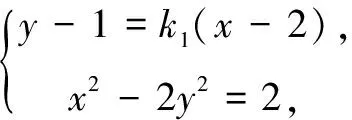
由k1+k2=0,得直線PQ的斜率

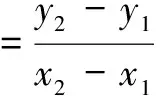
評注由kAP+kAQ=0聯(lián)想到設(shè)出直線AP,AQ方程,聯(lián)立雙曲線方程求出點(diǎn)P,Q的坐標(biāo),再由直線斜率的定義直接求定值,也是常見方法.但此法適用的前提是直線與雙曲線的兩個(gè)交點(diǎn)之一已知,利用韋達(dá)定理的積式可求另一交點(diǎn),運(yùn)算量同樣大.

由同一點(diǎn)出發(fā)的雙曲線的兩條割線(形似),應(yīng)當(dāng)具有類似的性質(zhì),如直線的方程、交點(diǎn)的坐標(biāo)等相似性.以此為基礎(chǔ),可從函數(shù)與方程的角度出發(fā),構(gòu)造同構(gòu)方程解決問題.

解法3(利……