賞析函數性質的應用之美

李加軍 馬麗麗

(北京市第一0一中學懷柔分校,101407) (山東省濰坊市第七中學,261021)

2017年版《普通高中數學課程標準》明確指出，在學習數學和應用數學的過程中,學生能發展數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析等數學學科核心素養.數學核心素養是數學課程目標的集中體現,是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現,是在數學學習和應用的過程中逐步形成和發展的.六大數學核心素養既相對獨立、又相互交融,構成一個有機的整體,集中體現數學課程目標,反映當前數學課程改革的主要方向和目標.

奇偶性、單調性、周期性、對稱性是函數的常用的基本性質.在數學解題中,充分發現、分析、利用這些性質,既可以快速巧妙地解決問題,又可以感受到數學給人帶來的魅力和愉悅,有助于提升學生的數學學科核心素養.

一、求函數值或最值

(A)8 (B)4 (C)-4 (D)-8

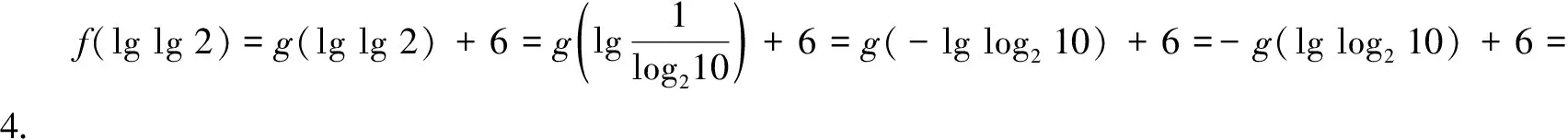
評注上述兩題中f(x)滿足f(x)=g(x)+c,其中g(x)是奇函數,c為常數,而所研究函數值對應的兩個自變量互為相反數,利用奇函數g(x)滿足g(x0)+g(-x0)=0,可知f(x0)+f(-x0)=2c.

評注在上述兩題中,從表面上看不易發現函數f(x)的性質,此時通過運算進行大膽合理的等價變形,使得f(x)滿足f(x)=g(x)+c,其中g(x)是奇函數,c為常數,則根據奇函數g(x)滿足gmax(x)+gmin(x)=0,可知fmax(x)+fmin(x)=2c.

二、求解方程

例5(2013年復旦大學自主招生題)已知ex=4-x,lnx=4-x的兩個解分別是x1,x2,則x1+x2=______.

解令f(t)=et+t-4,則f(t)在R上是單調增函數.又ex1+x1-4=0 且lnx2+x2-4=0,即eln x2+lnx2-4=0,所以f(x1)=f(lnx2),有x1=lnx2,進而有x1+x2=x2+lnx2=4.

例6(2012年河南預賽題)若α是方程xex=2 011的解,β是方程xlnx=2 011 的解,則αβ=______.

解令f(t)=tet,易知f(t)=tet在(0,+∞)是單調……