一道解析幾何壓軸題的分析與思考*

毛志偉 王 耀

(江蘇省揚州大學數學科學學院,225002) (江蘇省蘇州市第一中學,215000)

一、試題呈現

(1)求橢圓C的標準方程;

(2)若直線MN的斜率k=1,求定點A的坐標.

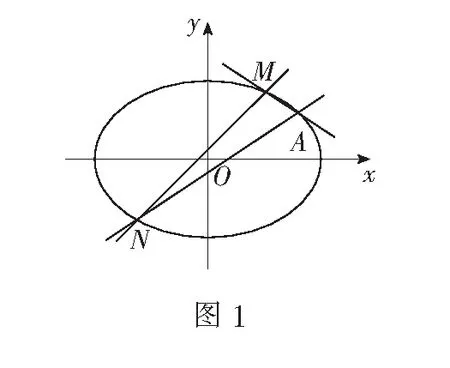
本題是2022年蘇錫常鎮四市高三一模解析幾何壓軸題.問題以斜率關系為背景,探究定點、定值問題,考查學生數學綜合運用能力和數學運算素養.縱觀近幾年高考、模考試題,筆者認為此類問題具有一定的代表性,且解法靈活,具有一定的研究價值.因此筆者通過解法思考與優化、一般性結論探究及應用,多維度揭示問題本質,幫助學生積累經驗,提升數學解題能力.

二、解法探究

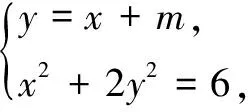
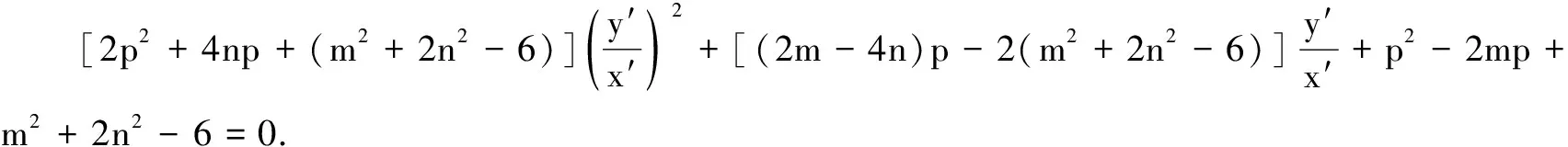
故點A的坐標為(2,1).

三、錯解及反思

筆者發現部分同學審題不仔細,想當然地認為點A在橢圓上,利用直線AM,AN的斜率分別為k和-k,計算出點M,N的坐標,最終也能得到正確的結果.具體過程如下.

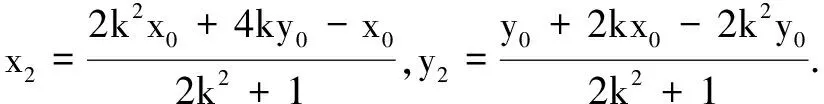
評注命題者在設計這道題時,也是精心構思的.從邏輯上看,該解法是不完整的,點A可以在橢圓上(如上述方法),也可能在橢圓外(利用上述解法是難以排除的).但禍兮福之所倚,通過該解法可發現如下一般的結論(證明見后面結論3).

錯解2設直線MN:y=x+m,點M(x1,y1),N(x2,y2).由kAM=-kAN,設直線AM:y=k(x-x1)+y1,直線AN:y=-k(x-x2)+y2.

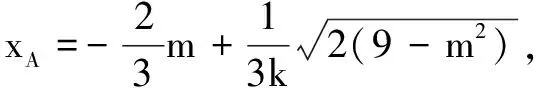
評注回看錯解2,當m=-3時,判別式Δ=0,點M與N重合,即直線MN與橢圓相切,切點為(2,-1),斜率之和為0可看成正無窮與負無窮之和.該解法雖然存在問題,但此解法中也蘊含著如下結論.

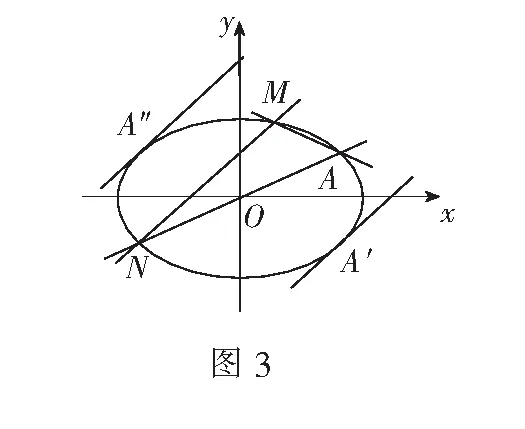
設點M(x1,y1),N(x2,y2),直線AM與AN的方程分別為y=k(x-x0)+y0,y=-k(x-x0)+y0.

四、結論探究及應用

同前文利用齊次化方法探究點的坐標,也可以利用齊次化方法探究斜率關系,得到如下……