向量投影在圓錐曲線問題中的應用舉隅

魏東升

(福建省廈門雙十中學漳州校區，363107)

隨著新課標在中學教學的實施,向量成了高中數學的重要組成部分,而其工具性也讓向量問題成了高考的熱點之一.根據向量數量積的定義,其幾何意義是指其中一個向量的模與另一個向量在這個向量方向上投影的乘積.筆者在教學中發現,數量積中提及的向量投影的概念,在解決許多有關求最值(或求值、求范圍)的各類問題中有著重要作用.本文以筆者所在學校高三模考中一道解析幾何題為引例,窺視向量投影在問題求解過程中發揮的神奇功效.

一、引例與解答

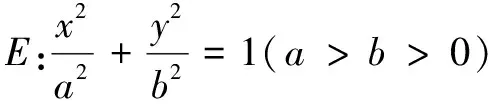
(1)求E的方程;

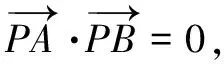
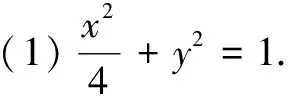
(2)解法1(常規解法)

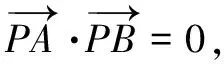
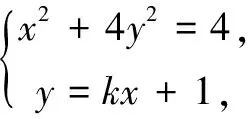
聯立直線AQ與BP的方程,消去y可得

解法2(利用向量投影)

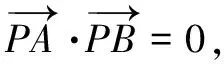
解法3(利用向量投影)

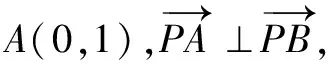
向量在對圓錐曲線中核心條件的轉化上往往具備天然的優勢,而向量的投影就是體現這種優勢的有力證據之一.以下進一步舉例說明.

二、向量投影的應用舉例

1.利用投影處理定值問題

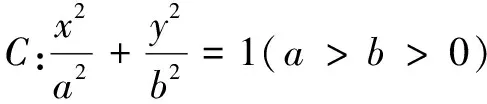
(1)求C的方程;

(2)設直線y=kx+m(m>0)交y軸于點M,交C于兩不同點A,B,點N與M關于原點對稱,BO⊥AN交AN于點Q.問是否存在定點M,使|NQ||NA|為定值？

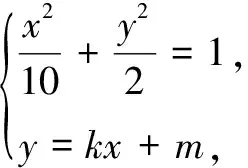
令Δ=(10km)2-4(1+5k2)(5m2-10)>0,解得m2<2+10k2.

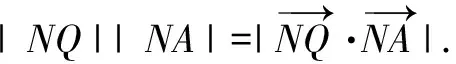
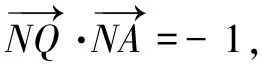
2.利用投影處理取值范圍問題

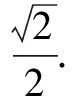
(1)建立適當的坐標系,求C的方程;

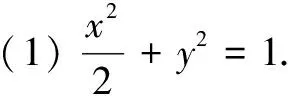
(2)如圖1，因為直線AB與以OA為直徑的圓的一個交點在圓O上,所以直線AB與圓O相切.

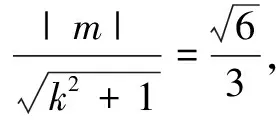
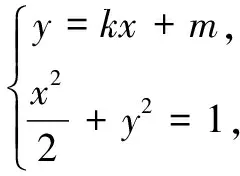
(2k2+1)x2+4kmx+2m2-2=0,

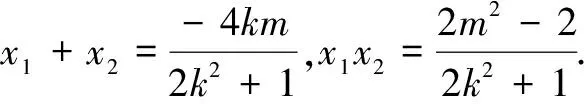
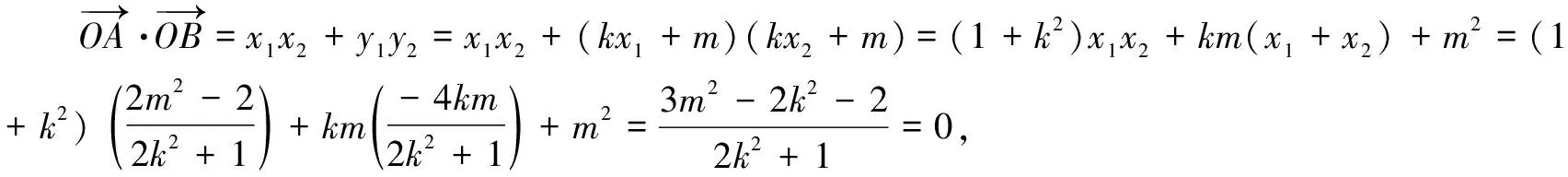
3.利用投影處理最值問題

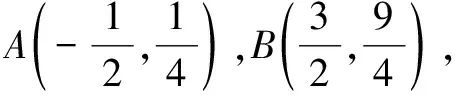
(1)求直線AP斜率的取值范圍;

(2)求|PA||PQ|的最大值.

解(1)(-1,1)(過程略)

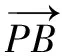
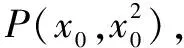
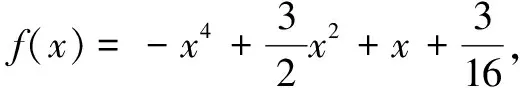
評注此題也可先求出點Q的坐標,再通過兩點間距離公式分別求出|PA|和|PQ|,從而得到|PA||PQ|的表達式,但計算量較大.實際上,解析幾何問題往往對學……