推廣圓錐曲線的一個(gè)定點(diǎn)定值命題

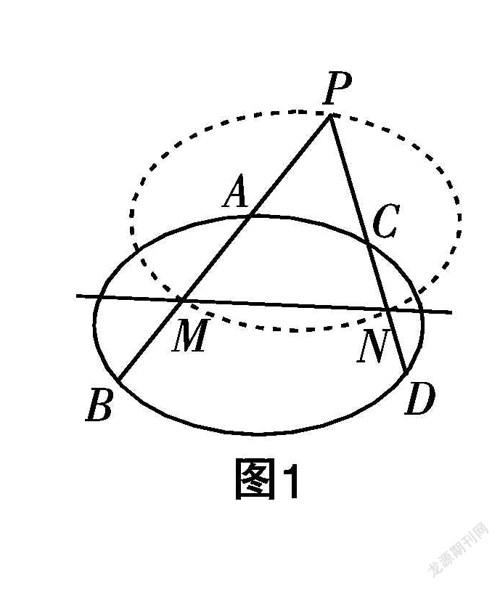
［摘? 要］ 文章通過對(duì)圓錐曲線的一個(gè)定點(diǎn)問題的探究，得出該問題的一般形式，并且以此為基礎(chǔ)，經(jīng)過類比遷移，解決了另一個(gè)與之相關(guān)的定值問題.

［關(guān)鍵詞］ 圓錐曲線；定點(diǎn)定值；推廣

命題研究的一個(gè)樸素目標(biāo)是對(duì)命題的結(jié)論部分不斷加強(qiáng)，對(duì)命題的條件部分不斷減弱，從而獲得命題更為深刻的形式；命題研究的最終目標(biāo)是為了更好地理解命題，使得原本略顯突兀的命題最終變得簡(jiǎn)單自然. 兩者相輔相成，命題的深刻形式有益于認(rèn)識(shí)命題的本質(zhì)特征. 本文探討吳世星老師提出的一個(gè)命題，通過對(duì)條件進(jìn)行減弱，最終得出這一命題的一般形式.

吳世星老師在文［1］對(duì)一道解析幾何中的拋物線試題進(jìn)行了深入探討，運(yùn)用類比思想最后得出橢圓和雙曲線中也有類似的結(jié)論成立，概括如下：

緊接著，吳世星老師對(duì)命題1進(jìn)一步思考后發(fā)現(xiàn)可以對(duì)圓錐曲線這一定點(diǎn)定值命題的結(jié)論部分進(jìn)行推廣，給出了橢圓和雙曲線兩種情形的命題表述，概括如下：

從這一角度來看，命題1其實(shí)是對(duì)中學(xué)數(shù)學(xué)教師討論多年的圓錐曲線對(duì)定點(diǎn)張直角弦過定點(diǎn)問題的逆向思考. 事實(shí)上，鄒生書老師已經(jīng)在文［2］中指出：圓錐曲線對(duì)定點(diǎn)張直角弦過定點(diǎn)的逆命題是成立的（關(guān)于這一問題的推廣最為徹底的是許書華老師在文［3］中提出的）. 可見文［1］提出的命題1并非新命題.

繼續(xù)考察文［1］提出的命題2，從吳世星老師證明命題2的過程來看，文［1］限制“點(diǎn)M在圓錐曲線……