Prony級數的不同階數對HTPB推進劑力學響應仿真影響①

賈樂凡，史宏斌，沙寶林，許 楊

(西安航天動力技術研究所，西安 710025)

0 引言

HTPB推進劑被廣泛用于各型航天器、空間飛行器固體發動機上[1]。其力學響應行為與溫度、加載方式、加載歷程等諸多因素相關[2]。國內外針對HTPB推進劑本構方程進行了大量研究。HTPB推進劑基于本身的高填充比和固化彈性體結構表現為典型的非線性粘彈性復合材料，此類材料在應變較大時呈現明顯的應力-應變非線性特征[3]。針對HTPB推進劑本構方程的建立方法主要包括單獨使用彈性/粘彈性/超彈性模型[4-5]、彈性模型耦合蠕變模型[6-7]、粘彈性模型耦合超彈性模型[8-9]。此外，還有HTPB推進劑本構方程耦合塑性模型[10]、老化模型[11]、損傷模型[12]等其他模型的研究。目前，大部分本構方程建立的核心是表征HTPB材料的粘彈性響應特征。而Prony級數方程作為一種較為簡單的線性粘彈性本構方程得到了廣泛應用。在基于Prony級數的模型建立過程中，首先需要確定Prony級數階數，隨著Prony級數階數增高，其占用的計算資源呈指數增加。因此，在實際應用過程中Prony級數階數并非越高越好，而要結合數值模擬目的與計算資源現狀選取合適的Prony級數的階數。一般工程計算中這一取值由經驗給出，未見針對不同階數的Prony級數對數值模擬結果影響的專門研究。

本文根據試驗獲得HTPB松弛模量主曲線，建立其5～10階Prony級數模型并進行數值模擬，探究不同階數的Prony級數對HTPB推進劑數值模擬研究產生的影響，并嘗試給出不同情況下適用的級數階數。所得結論可應用于HTPB推進劑相關數值模擬研究，為其相關工程應用提供借鑒。

1 粘彈性本構方程

對于簡單的粘彈性材料，其應力-應變曲線與時間具有相關性。在此基礎上，如果其本構關系符合疊加性原理：

σ(ε1+ε2)=σ(ε1)+σ(ε2)

(1)

以及齊次性原理：

σ(βε)=βσ(ε1)，(β=const)

(2)

則可將其視為線性粘彈性材料。

對于簡單的線性粘彈性材料，其應力與應變歷史有關：

(3)

式中E(t)為松弛模量，通過定應變試驗測得。

對于與溫度相關的線性粘彈性材料，需要在積分中將溫度依賴項與時間依賴項分離：

(4)

式中ξ為縮減時間。

(5)

式中αT為時間-溫度平移因子，是關于溫度的函數，其值通過定應變試驗擬合而出。

目前，常用的線性粘彈性模型主要包括Maxwell模型、Voigt模型等[13]。其中，Prony級數模型，作為一種廣義Maxwell模型在工程上應用最廣。該模型可視為一個胡克彈簧與若干個Maxwell模型并聯，其階數可等效視為并聯的Maxwell模型個數。常用的Maxwell模型可視作1階Prony級數模型。無量綱形式的Prony級數為

(6)

式中gR(t)為無量綱松弛模量；N為方程階數；τi為材料的松弛時間。

對基于Prony級數的粘彈性本構方程，其數值計算結果與其階數N有關，在實際應用過程中，需結合數值模擬目的與計算資源現狀選取合適的級數階數。本文針對HTPB推進劑粘彈性本構方程，研究不同階數對其數值模擬研究產生的影響。

2 數值模擬

2.1 物理模型

通過單向拉伸試驗得到的HTPB推進劑應力-應變曲線，獲得其松弛模量主曲線，如圖1所示。

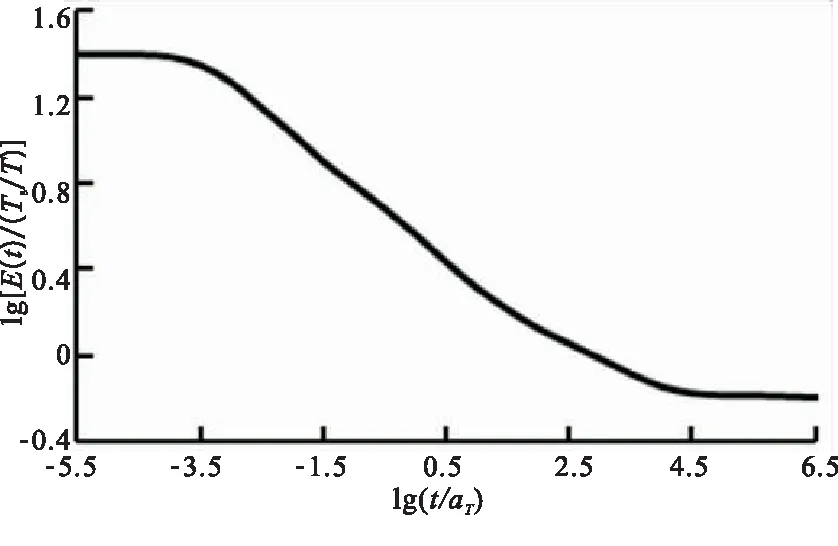
圖1 THPB應力松弛模量主曲線(Ts=293.15K)

根據松弛模量主曲線及時間-溫度平移因子擬合得到無量綱Prony級數各階的松弛模量系數，如表1所示。以表1數據作為材料模型，根據單軸拉伸試驗標準建立數值仿真模型。圖2為試件幾何尺寸，圖3為其模型示意圖。

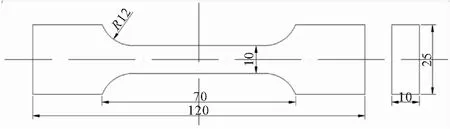
圖2 試件模型(單位：mm)

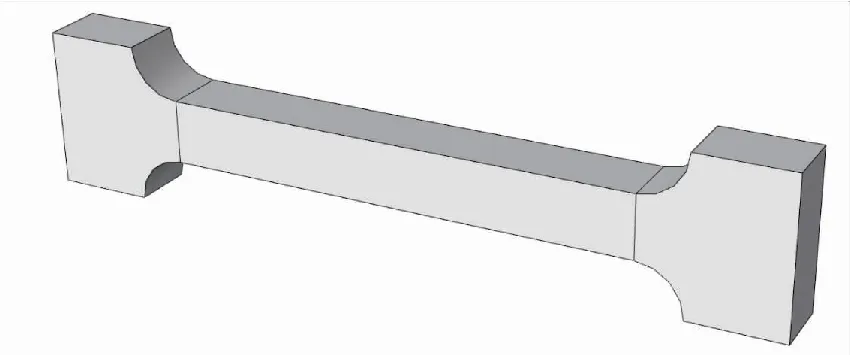
圖3 啞鈴形試件模型示意圖

表1 各階Prony級數參數

分別將5～10階Prony級數方程作為試件材料參數代入，對模型一端施加固定邊界條件，另一端施加60 mm位移邊界條件。分別設置分析步時間間隔為3600、360、36、12、7.2 s，以模擬試件在試驗時所經歷各拉伸速率下的力學響應得到其應力-應變曲線，并與試驗結果進行比對。

2.2 仿真結果

圖4為Prony級數取5～10階時模型在1、10、100、300、500 mm/min拉伸速率下的應力-應變曲線。

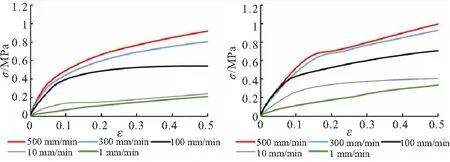
(a)N=5 (b)N=6

由圖4可以看出，各階級數模型仿真結果均隨拉伸速率增高而增大。在5階時，模型在500 mm/min拉伸速率下應力最大值約0.79 MPa，在1 mm/min拉伸速率下應力最大值僅有0.15 MPa；當拉伸速率較低時，其曲線斜率變化不大，而當拉伸速率較高時，其整體拉伸曲線呈現典型的雙線性特征。這是因為Prony級數模型在較短時間歷程的拉伸過程中主要表現彈性體特征，而在較長時間歷程內表現蠕變特性。

此外，綜合分析各階級數仿真結果可以看出，拉伸速率較高時，各階Prony級數仿真結果較為接近；在拉伸速率較低時，Prony級數階數越高，低拉伸速率下仿真結果越大。這是因為在拉伸速率較低(1 mm/min或10 mm/min)時，模型的力學響應受蠕變特性影響較大，高階Prony級數能夠更好地模擬材料的蠕變行為。因此，其結果隨階數升高而增大。

3 試驗結果與討論

3.1 試驗儀器與方案

試驗儀器為深圳三思縱橫UTM520HB電子萬能試驗機，試驗對象為依照QJ 924—1985《復合固體推進劑單向拉伸試驗方法》[14]制成的某配方HTPB推進劑試件，其配方如表2所示。

表2 HTPB推進劑配方

在20 ℃條件下進行拉伸速率為1、10、100、300、500 mm/min的HTPB推進劑單軸拉伸試驗，得到試件的應力-應變曲線。

3.2 試驗結果

試驗在每個拉伸速率下均進行3次。其中，除一組試件在300 mm/min拉伸速率下提前斷裂(分析排除試驗設計原因)外，其余各組在相同拉伸速率下的結果均十分接近。在兩組完整數據中，選取一組結果作為后續數值模擬研究參考。試驗獲得的HTPB推進劑不同拉伸速率下應力-應變曲線如圖5所示。可以看出，HTPB推進劑在不同拉伸速率下表現出明顯的粘彈性特征，其應力應變與加載歷程有關；在同樣拉伸應變下，應力隨應變率的增大而增大。

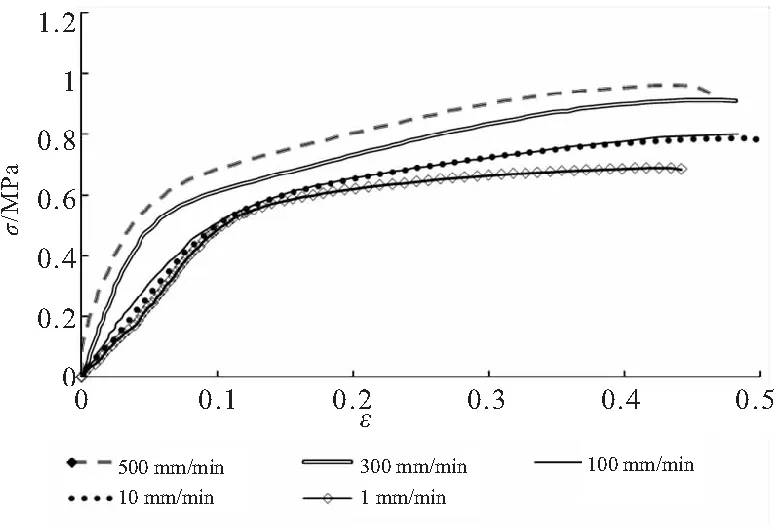
圖5 不同拉伸速率下推進劑應力-應變曲線

結合試驗結果可以看出，粘彈性材料拉伸過程中，應力-應變曲線與拉伸速率有關，需要分析不同拉伸速率對各階Prony級數方程數值模擬結果的影響。

圖6為不同拉伸速率下的各階Prony級數模型仿真結果與試驗結果對比。比較不同拉伸速率下的試驗與數值模擬結果看出，不同拉伸速率下Prony級數模型仿真結果均隨階數的增高而向試驗結果逼近，這是因為高階的Prony級數模型能夠更好地反映材料模型的實際力學特性。

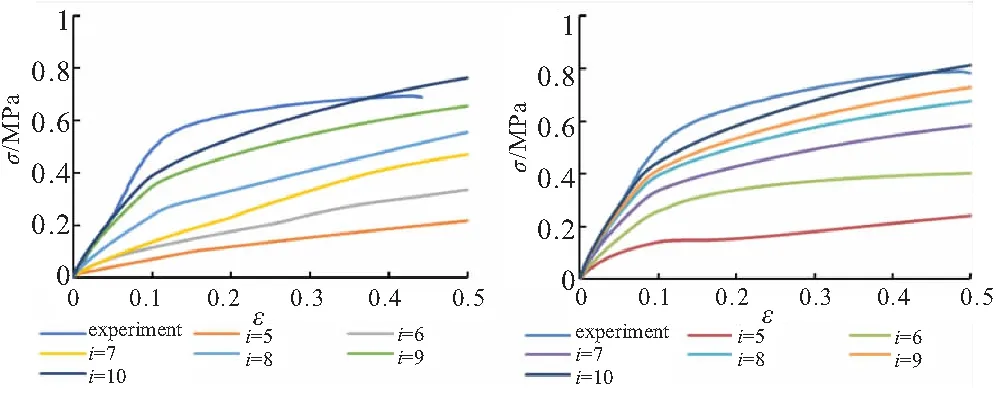
(a)1 mm/min (b)10 mm/min

由圖6可見，當拉伸速率較高時，各階Prony級數模型結果差別不大；而當拉伸速率較低時，仿真結果誤差隨著階數降低而快速增大。這是因為Prony級數模型瞬時響應呈現彈性體特征，而時間效應呈現粘性體特征。當拉伸速率較高時，材料主要表現彈性效應，因此不同階模型結果差異較小；而當拉伸速率較低時，高階級數模型能夠更好地表征材料的粘性響應，因此高階模型相比低階模型誤差明顯減小。此外，可以看到試驗中試件相較仿真總是更早進入損傷階段。這是因為相比于實際情況，仿真模型無法反映試件在成型過程中的微觀缺陷或損傷，因此其結果更加理想化。

3.3 不同拉伸速率下各階Prony級數模型仿真誤差比較

在單軸拉伸試驗中，其應力通過測力裝置讀數除以截面面積計算得到，為試驗原始數據。因此，以試驗所測得應力值作為基準分析模型仿真誤差，取每一有效試驗應力數據點與各個仿真結果應力數據點距離最小值為其誤差，由此得出不同拉伸速率下的各階Prony級數模型仿真誤差。

圖7反映了不同拉伸速率下各階模型仿真誤差之間的關系。可以看出，不同拉伸速率下Prony級數模型仿真誤差總體上均隨階數的增高而減小。當拉伸速率較低時，階數對仿真誤差的影響尤為明顯，階數過低時，其平均相對誤差甚至大于50%。隨著拉伸速率的增大，仿真誤差對階數取值的敏感性逐漸降低。當拉伸速率在100 mm/min以上時，其各階平均相對誤差均能保持在15%以內。因此，當需要計算的物理情形下應變率較高(拉伸速率較高)時，可以適當降低模型的階數來提高計算效率，而當應變率較低(拉伸速率較低)時，需要適當提高模型階數來保證計算結果精度。

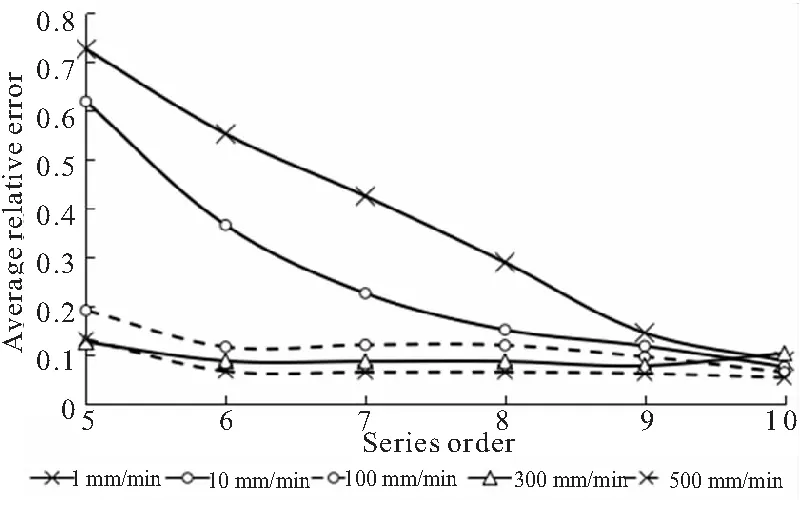
圖7 不同拉伸速率下各階級數仿真誤差比較

進一步觀察數據可以看出，拉伸速率較低時，低階方程誤差極大，但其誤差隨著階數增高迅速減小；當階數達到10階時，模型仿真誤差受拉伸速率變化影響較小。各階方程誤差大體上隨拉伸速率增大而減小，同一拉伸速率下的方程誤差大致上隨階數增高而減小。當拉伸速率較低時，小于9階的方程誤差較大，不能符合實際情況；當拉伸速率較大時，6階以上的模型誤差均相對較小，但考慮到實際仿真時的情況，即使拉伸速率較大時，基于Prony級數的粘彈性模型階數也應取不小于7階。

4 結論

(1)利用Prony級數計算HTPB推進劑粘彈性力學響應時，其階數最好不小于7階；在小于7階時，模型數值仿真計算結果誤差大多偏離試驗數據10%以上，與材料實際力學行為有較大差異；當計算貯存、運輸等緩慢加載工況時，其階數最好不小于9階。

(2)當拉伸速率較高時，各階級數仿真結果與試驗相差較小，但隨著拉伸速率下降，低階Prony級數的仿真誤差迅速增大。

(3)當拉伸速率較高時，可采用較低階數的Prony級數模型以提高計算效率；而當拉伸速率較低時，需要采用高階Prony級數方程以更好地模擬材料蠕變特性。

本文結論適用范圍為未進入損傷階段的HTPB推進劑。其結論可用于HTPB推進劑的簡單工程計算及強度校核，并為其安全裕度設計及失效判定提供理論依據。