基于組合賦權法-云模型的裝備保障能力評估研究

翁興卓，王海青，薛勇，孫金，何能波

（航天工程大學，北京 102206）

隨著武器裝備由機械化向信息化的快速發展，各類信息化裝備不斷列裝，其保障能力的高低直接關系遂行任務的作戰結果，通過開展裝備保障能力評估，建立合理的指標體系，選取科學的評估方法，可以有效檢驗裝備保障能力水平的發揮，進而找準短板弱項，為裝備保障能力建設提供借鑒參考。

1 評估指標體系的構建

評估指標體系的構建是裝備保障能力評估的基礎，是開展能力評估工作的必要前提，在查閱大量文獻資料及法規制度的基礎上，結合部隊實際，以目的性、全面性、客觀性與實用性為原則，選取指揮決策能力、維修保障能力、裝備保障訓練能力、物資器材保障能力、裝備管理保障能力5個一級指標，共下設15個二級指標的評估指標體系，見表1。

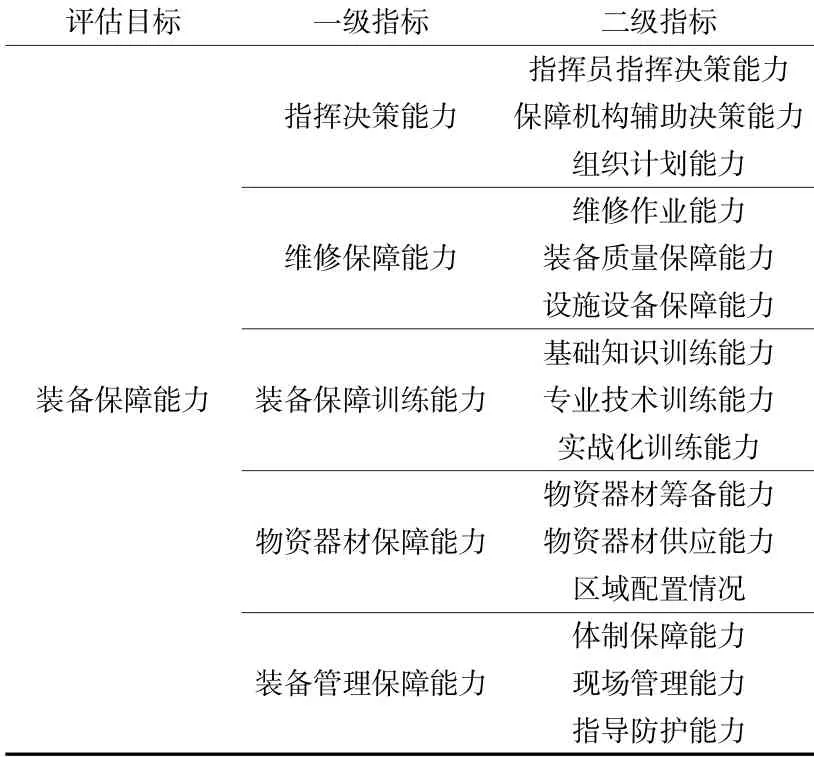
表1 裝備保障能力評估指標體系

2 評估指標體系權重確定方法

2.1 主觀權重的確定

層次分析法（The Analytic Hierarchy Proeess）由美國運籌學家Satty.TL提出，其原理是對各評估指標間重要性兩兩比較確定之間的邏輯順序，通過簡便的數學運算，將復雜系統分層級進行有效處理，實現定性與定量處理的有機結合，簡潔實用，可操作性強[1]。其基本步驟如下：

（1）構建層次結構

對評估目標進行全面、系統的分析，根據分析將評估目標所涵蓋的因素分類處理，結合因素屬性的差異、相互作用關系，建立一個由若干層次組成、層級間相互關聯作用的結構模型。

（2）構建判斷矩陣

采用1-9標度法，對每一層指標下的各個指標采取兩兩比較的方式確定其判斷矩陣：A={aij}，i，j＞0，aij=1/aij，賦予其“重要性”數值，用于定量計算。

（3）指標權重的計算

采取和積法計算權重，首先將矩陣每列元素正規化處理，將矩陣中各行元素求和：

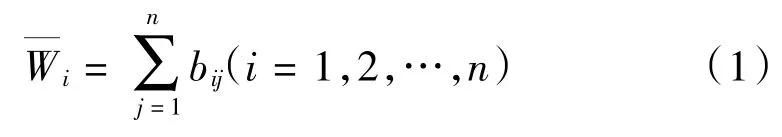
再規范化處理：

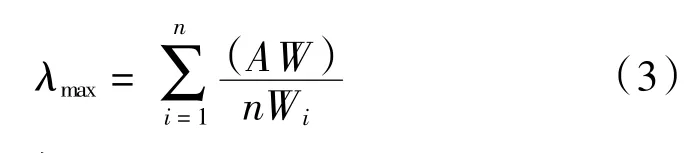
（4）一致性檢驗

計算檢驗矩陣一致性指標CI：

根據矩陣階數n，對照平均一致性指標RI，RI對照表如表2所示，計算一致性比值CR：

表2 平均一致性檢驗指標

若CR＜0.1，則符合一致性檢驗要求，反之，邀請專家重新構造判斷矩陣，直至CR通過一致性檢驗要求。

2.2 客觀權重的確定

變異系數法可根據各評估指標的數據信息，通過數學計算方法對數據信息進行處理，從而得到權重，其基本原理是根據各評估指標的差異程度來衡量其重要程度，評估指標差異程度越大，權重比例越高，且可以有效解決評估指標之間量綱不同而造成的差異[2]。其基本步驟如下：

（1）變異系數的計算

通過計算各評估指標的變異系數：

用以消除量綱不同帶來的影響，準確的反映其差異性[3]，其中σi為第i個指標的標準差，為第i個評估指標的均值。

（2）指標權重的計算

評估指標權重：

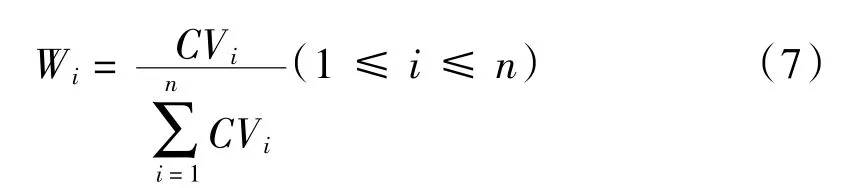
2.3 組合權重的確定

鑒于層次分析法與變異系數法均具有一定的局限性[4]，采取組合賦權法確定指標權重，設層次分析法計算出的主觀權重為WA=[wa1，wa2，wa3，…，wam]T，變異系數法計算的客觀權重為W變=[w變1，w變2，w變3，…，w變m]T，采取乘數符合歸一法計算WA與W變復合權重為：

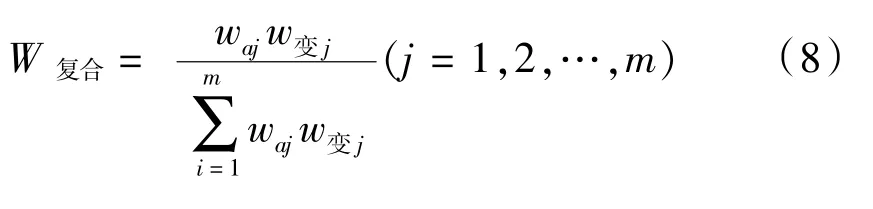
3 基于云模型的裝備保障能力評估方法設計

通過云模型的構建，用隨機云滴的確定度反映評估語言的模糊性，有效的打破了兩者在隨機性和模糊性表達上的局限，實現定性與定量之間的相互轉換，評估結果更為直觀[5]。

3.1 云發生器

將評估的樣本通過逆向云發生器將定量數據轉換為定性概念，計算步驟如下：

（1）根據樣本數據計算均值：

（2）計算方差：

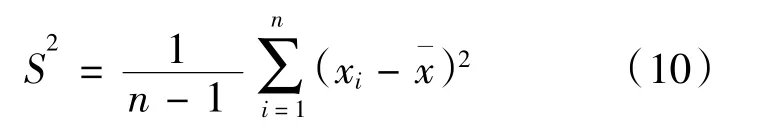
（3）計算熵、超熵：

輸入樣本的云特征向量（Ex，En，He），通過正向云發生器生成云圖，算法步驟如下：

e為方差。

（2）生成高斯隨機數：x～N（Ex，），Ex為期望值，為方差。

（4）重復上述步驟，生成N個云滴。

3.2 評估標尺云的確定

咨詢裝備保障領域專家意見，將評估等級劃分為5個等級，即：V={V1，V2，V3，V4，V5}，分別對應“非常差”“差”“一般”“良好”“優秀”，“非常差”“優秀”2個評估等級在評估中評價者對其概念判斷較為精準，而對“差”“一般”“良好”3個評估等級的概念判斷較“非常差”“優秀”來說，相對模糊，故采取黃金分割法確定標尺云，使得單邊約束評語較中間3個評語的取值相對較窄，更符合裝備保障評估的實際。其云數字特征見表3。

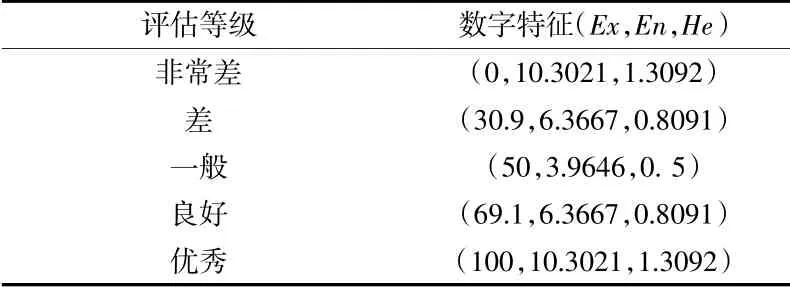
表3 評估標尺云數字特征

3.3 評估指標云的計算與云相似度計算

邀請專家對所有三級評估指標進行打分，獲取專家打分值后，根據逆向云發生器的算法，得到各項二級評估指標的云數字特征，而后計算其上層指標的云數字特征，計算式：

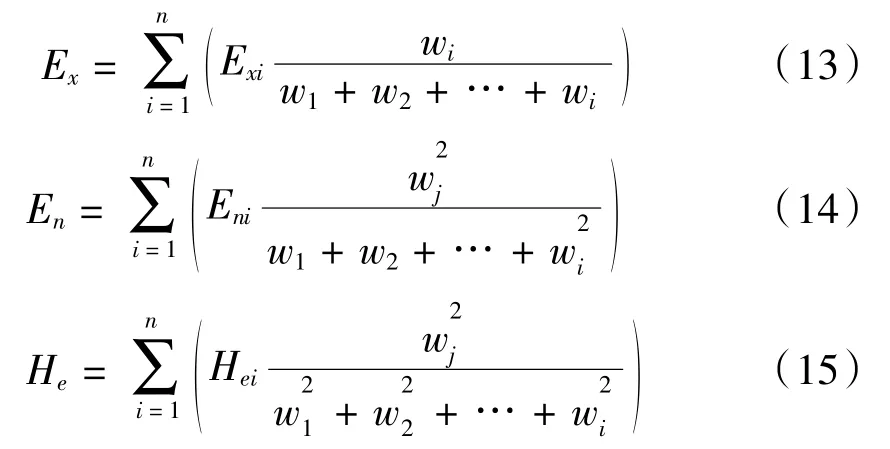
通過上述對評估標尺云的確定，結合評估指標云及評估綜合云的計算，得到其各層評估指標的數字特征及云圖，采取加權歐式距離計算各評估指標云與評估標尺云之間的相似度，步驟如下：

（1）（Ex，En，He）為評估指標云的數字特征，評估標尺云的數字特征為兩者間距離計算式為：

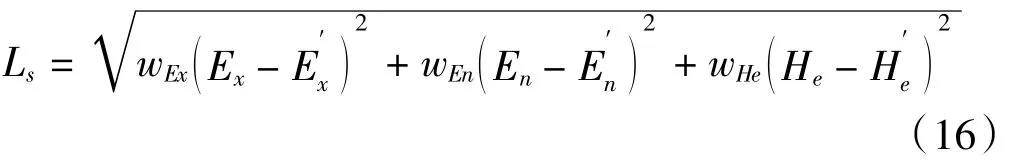
其中w為云數字特征權重，且wEx+wEn+wHe=1

（2）各評估指標云與評估標尺云相似度閾值為：

（3）各評估指標對評估標尺云的相似度為：

通過評估指標生成的云圖及與評估標尺云的相似度，最終確定評估等級。

4 實例應用

以某單位某次實兵演習裝備保障為例，根據式（1）～（8）計算主、客觀權重及組合權重，計算結果如表4所示。

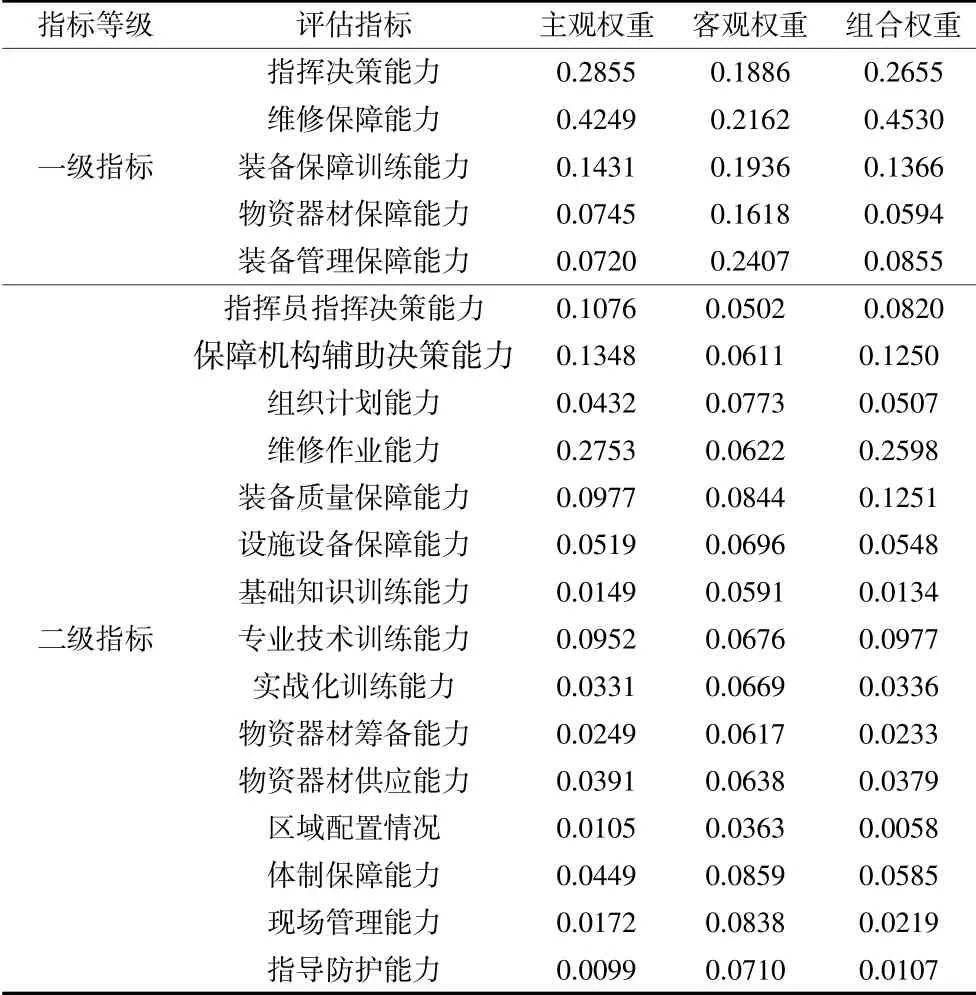
表4 評估指標權重數值

邀請10位裝備保障領域相關專家對本次裝備保障任務中15個二級評估指標進行打分，評估指標等級以評估標尺云為參考，打分區間為。將專家打分數據根據逆向云發生器算法公式（9）～（12）計算其數字特征，計算結果如表5所示。

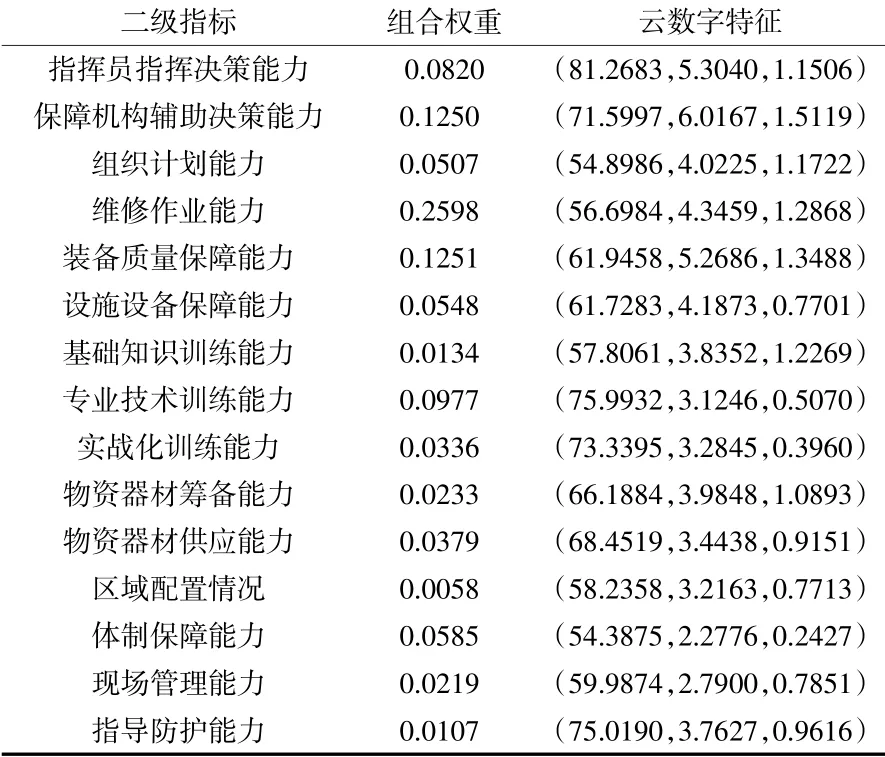
表5 二級評估指標云數字特征

將二級評估指標云數字特征及其組合權重運用公式（13）～（15），計算得到一級指標云數字特征，計算結果如表6所示。

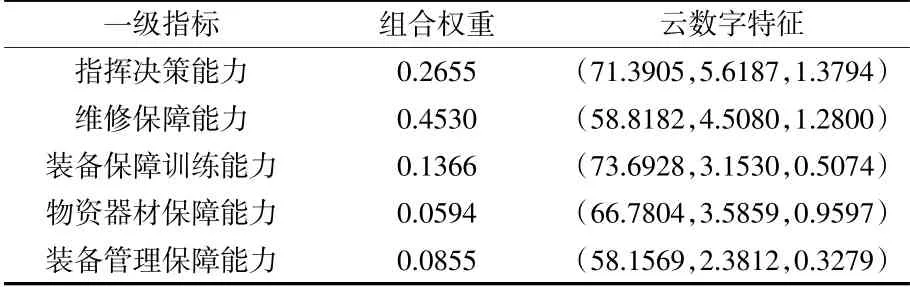
表6 一級評估指標云數字特征

最終計算得到裝備保障能力評估綜合云數字特征為（64.6044，4.6201，1.2292）。運用MATLAB軟件通過云正向發生器生成云圖，并將評估標尺云一并繪入圖中，生成評估綜合云圖，如圖1所示。

圖1 綜合評估云圖

按照云相似度計算式（16）～（18）計算綜合云與各評估標尺云的相似度，設云數字特征權重分別為wEx=0.5，wEn=0.25，wHe=0.25，計算結果如表7所示。

表7 綜合云相似度計算結果

由圖1可以看到，箭頭指處為裝備保障能力綜合評估云圖，可以直觀地看到其在評估標尺云圖上的分布在“一般”和“良好”等級之間，更趨近于“良好”等級，從表7計算結果來看，綜合云與評估標尺云各評估等級相似度分別為4.34%、8.34%、19.23%、60.19%、7.89%，和良好等級的相似度60.19%大于其他評估等級相似度，綜合可視化云圖及相似度計算數據，判定此次裝備保障能力綜合評估等級為“良好”。同理，可以確定一級指標指揮決策能力、維修保障能力、裝備保障訓練能力、物資器材保障能力、裝備管理保障能的評估等級分別為“良好”“一般”“良好”“良好”“一般”，表明此次實兵演習裝備保障活動實施過程中，裝備指揮決策能力、裝備保障訓練能力、物資器材保障能力較好，而維修保障能力、裝備管理保障能力需要進一步加強。

5 結語

針對裝備保障能力評估的諸多不確定因素，采取組合賦權法確定指標體系權重，并將云模型引入評估中，有效的打破了隨機性和模糊性表達上的局限，實現定性與定量之間的相互轉換，并以某單位某次實兵演習中裝備保障為例進行評估，確定評估等級的同時找準了影響裝備保障能力的短板弱項，有效的驗證該方法的可行性，為該單位裝備保障能力建設提供科學參考。