直管在橫向流體沖刷下的流固耦合分析

姜 超 梁鐵波 王昌朔 廖成宇 艾 陽

（中國核動力研究設計院核反應堆系統設計技術重點實驗室，四川 成都 610213）

0 引言

流致振動廣泛存在于管殼式熱交換設備中，流體沖刷傳熱管所造成的流致振動會對直管結構造成等幅循環載荷，且振動次數較大。當振動累積的疲勞損傷值達到傳熱管材料的臨界疲勞損傷值時，傳熱管就會發生破損。因此傳熱管的流致振動特性分析可為其使用壽命的預測提供參考。

近年來，隨著計算流體力學（CFD）技術的發展，國內外許多學者針對流體沖刷直管引發的流致振動現象做了很多研究。Williamson等人通過圓柱的渦激振動實驗，發現了2S、2P、2C之后第四種引起渦激振動的周期性漩渦尾流模式2T，這種模式是在每半個周期內形成三個漩渦，并且所有這些尾流模式都是反向對稱的。K.Lam等人基于表面渦模型和流固耦合方法，研究了低雷諾數橫流作用下的管束振動特性。陳德奇等人基于歐拉-伯努利梁理論，采用動網格技術，通過Fluent和Transient Structural實現帶格架5×5燃料棒束的雙向流固耦合計算，對其振動特性進行模擬研究。馮志鵬等人采用雙向流固耦合方法，并結合動網格技術對直管在內流、外流和內外流共同作用下沖刷直管的瞬態模擬計算，得到單向耦合與雙向耦合下直管的振動軌跡。喬永亮等人針對三維圓柱繞流問題，研究不同的湍流模型對計算精度的影響。趙穎杰等人在Workbench中用CFX和Transient Structural計算模塊對蒸汽發生器傳熱管的直管段進行了汽液兩相雙向熱流固耦合數值分析。徐楓等人采用數值方法，分別模擬了圓柱體和多種棱柱體在橫向流動中的流致振動現象，得到橫向和流向位移隨時間的變化曲線，研究發現圓柱中心的振動位移路跡大致為“8”字型。但目前針對不同的湍流模型對流致振動特性分析的研究還較少。

因此本文基于雙向流固耦合方法，針對不同的湍流模型，對直管在橫向流體沖刷作用下的流致振動特性進行了研究。結合不同流速工況下管中心位置的振動幅值及振動頻率，確定一種精度較高的流固耦合計算方法。

1 數值模型

對橫流沖刷直管的流致振動模擬，是建立在雙向流固耦合的基礎上，本研究采用Transition SST模型、Realizable k-e模型、低雷諾數k-e模型和LES模型分別對流體流動進行描述。

1.1 Transition SST模型

Transition SST四方程轉捩模型，是將SST kω兩方程湍流模型與另外兩個轉捩模型方程進行耦合，其中一個輸運方程描述轉捩流動的間歇因子γ，另一個方程描述從層流過渡到湍流的起始條件。

其中，SST k-ω關于湍流動能k和耗散率ω的輸運方程式為：

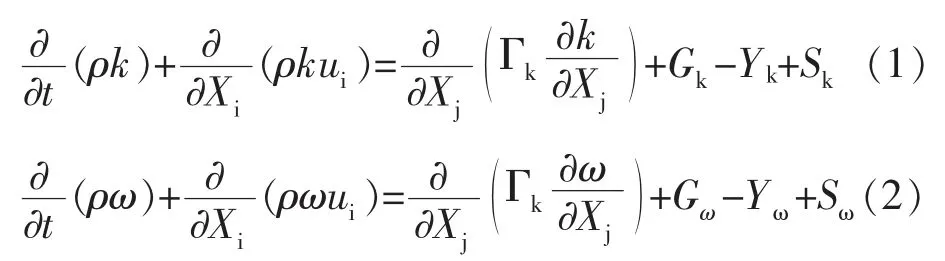
式中，G和G分別為k和ω的增量；分別為Γ和Γ的擴散系數；Y和Y分別為湍流引起的k和ω的耗散；S和S分別為k和ω的自定義源項。

其中，描述轉捩流動間歇因子γ的輸運方程式為：

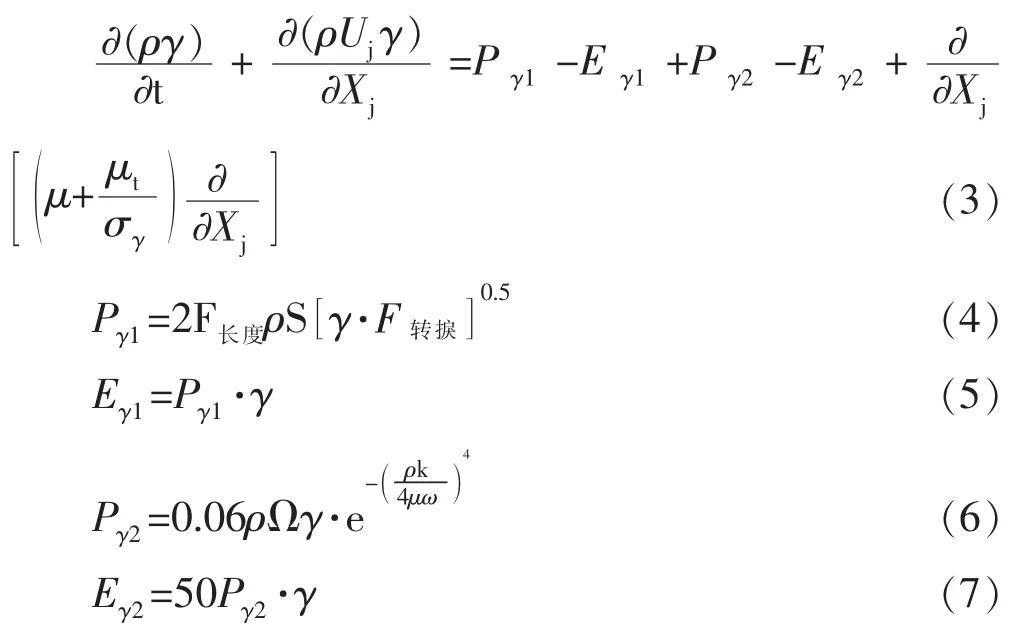
式中，S為應變速率的大小；Ω為漩渦強度；F為渦量雷諾數Re和動量厚度雷諾數Re的函數。

其中，描述轉捩開始位置的動量厚度雷諾數Re的輸運方程式為：

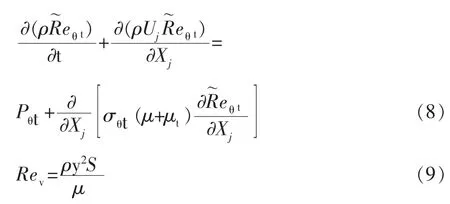
式中，y為沿法線方向到壁面的垂直距離。

1.2 Realizable k-e模型

Realizable k-e模型中，湍流動能k和耗散率ω的輸運方程為：

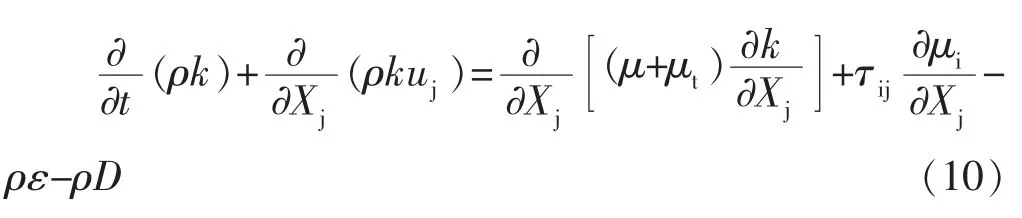
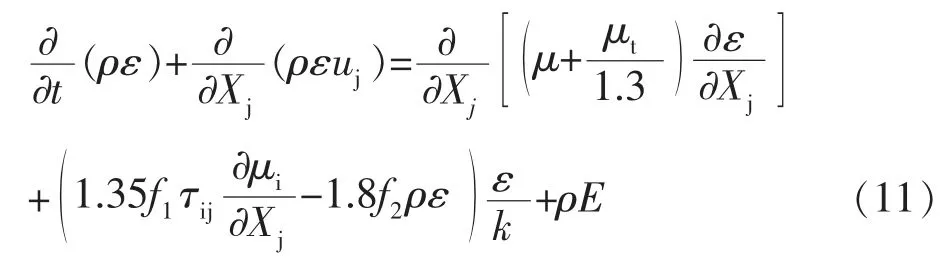
式中，μ為渦流粘度；f和f為阻尼系數；D和E分別為湍流動能k和耗散率ω的源項。

1.3 低雷諾數k-e模型

低雷諾數k-e模型的湍流動能k和耗散率ω的輸運方程與Realizable k-e模型形式相似，不同的是低雷諾數k-e模型中渦流粘度不是常數：

式中，C為常數；f為阻尼函數。

1.4 LES模型

LES模型是利用濾波的方法，對于大尺度的渦采用直接數值模擬求解，而對于其余各向同性的小尺度渦流則可用亞網格尺度模型采用雷諾平均方法進行求解。

動量方程形式如下：

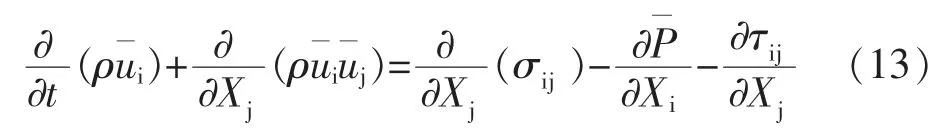
湍流應力張量表示亞網格尺度的應力：

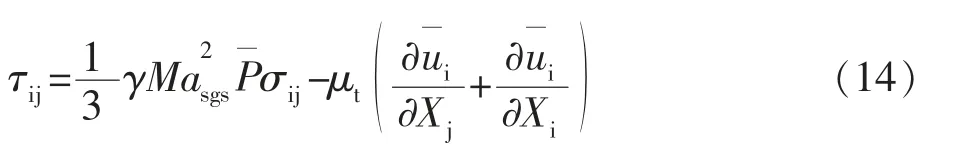
式中，μ為亞網格尺度下的湍流粘度；σ表示兩個正交單位向量的點積；Ma為亞網格尺度下的馬赫數。

2 物理模型及邊界條件

2.1 物理模型

數值計算的模型參數與David Schowalter的試驗參數保持一致，直管與流場的尺寸參數詳見表1。直管軸向與流場的長和高垂直，直管圓心到流體進口的距離為50mm，高度也是50mm，幾何模型如圖1所示。

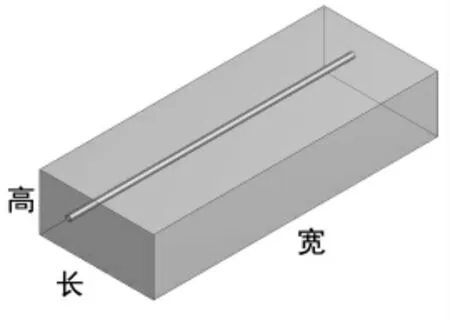
圖1 幾何模型示意圖

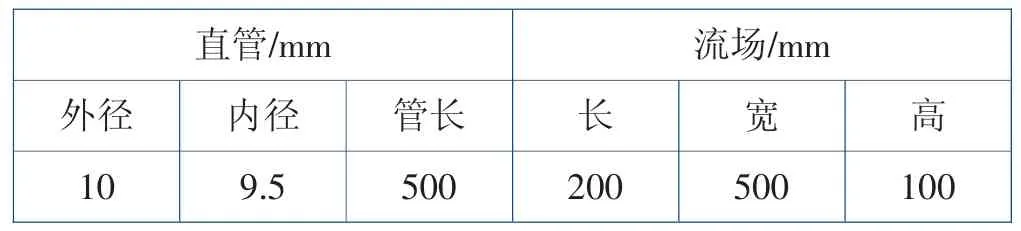
表1 直管與流場的尺寸參數

2.2 邊界條件

對于直管流致振動問題的數值求解，流場的入口類型為“速度入口”，出口類型為“壓力出口”。David試驗中所采用的無量綱流速u：

式中，無量綱流速u的取值范圍為1～6；u為來流速度；f為直管的一階固有頻s率；d為直管的外徑。

在穩態流場計算的基礎上進行結構的靜力學分析，然后再進行模態分析，得到直管固有頻率。直管的一階固有頻率f為173.6Hz。根據公式（15）可得試驗中來流速度u的范圍為1.74～10.42m/s，因此本文將入口流速范圍取為3～7m/s。

3 數值模型計算

3.1 流致振動特性計算

基于ANSYS Workbench平臺，采用動網格技術和雙向流固耦合計算方法，研究直管在3～7m/s流速范圍內的橫向沖刷下的流致振動特性，得到直管中心點沿來流方向（x方向）和垂直來流方向（y方向）上的振幅以及振動頻率。

以3m/s工況為例，進行網格無關性驗證計算。采用不同湍流模型，經流固耦合計算得到的直管中心點振幅及振動頻率。由網格無關性驗證計算可知，當網格數量增加至8.6萬時，Realizable k-e模型得到數值解不再隨網格數量變化；當網格數量增加至17.5萬時，低雷諾數k-e模型得到數值解不再隨網格數量變化；當網格數量增加至26萬時，Transition SST和LES模型得到數值解不再隨網格數量變化。

經過數值計算，得到不同湍流模型在3m/s來流速度下直管中心點的位移軌跡，并得到直管中心點在x和y方向上的振動幅值及振動頻率。位移軌跡如圖2所示。

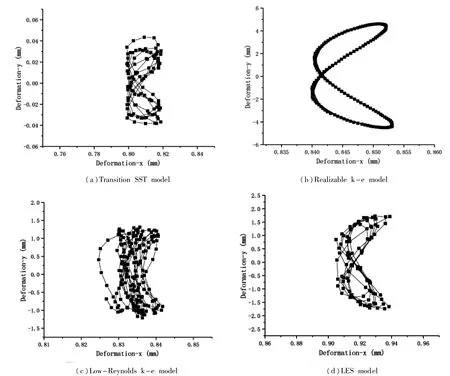
圖2 直管中心點的位移軌跡

綜合以上四種湍流模型在3m/s流速工況下流致振動的計算結果，發現采用Realizable k-e模型和LES模型計算振動更易達到收斂，得到的振動幅值也更加穩定。在3m/s流速工況下，直管的振動特性參數與David試驗值的對比詳見表2。

表2 直管振動特性參數

3.2 湍流模型適用性分析

此外，本文還選取4m/s、5m/s、6m/s和7m/s的入口流速，分別進行了流固耦合計算，得到不同工況下的直管流致振動特性。直管中心點在x、y方向上的振幅以及振動頻率見圖3～圖5。

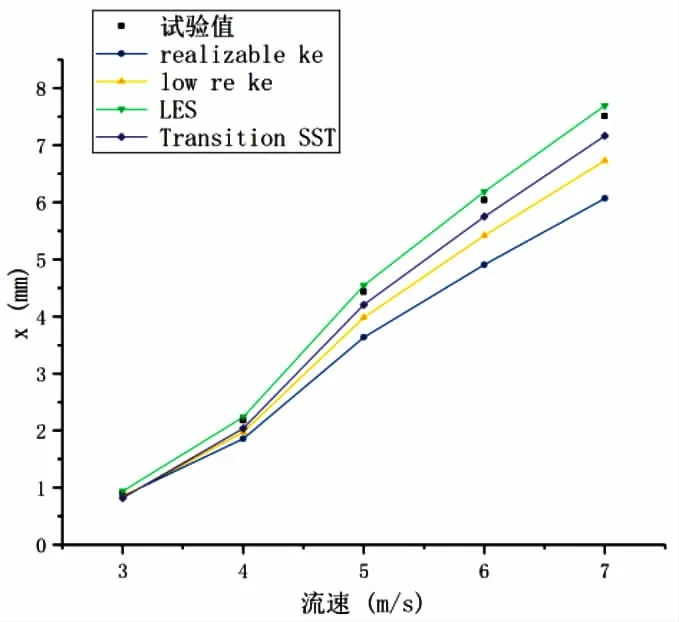
圖3 直管在x方向上的振幅

由圖3和圖4可知，在3～7m/s的流速范圍內，采用LES和Transition SST模型計算得到的直管中心點在x方向的振幅與試驗值最為接近，與試驗值之間的偏差分別為3.08%和10.11%；采用LES模型計算得到的直管中心點在y方向的振幅與試驗值之間的偏差最小，與試驗值之間的偏差為4.19%，而其他三種湍流模型顯然無法準確模擬出直管在y方向的振幅。

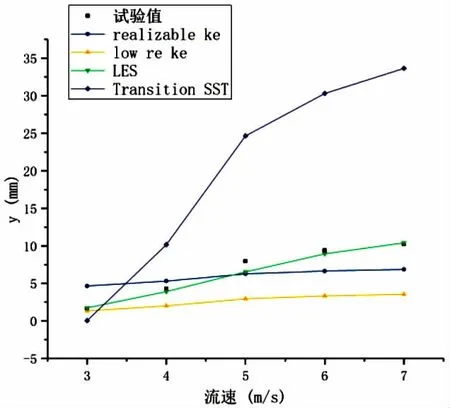
圖4 直管在y方向上的振幅

由圖5可知，在3～7m/s的流速范圍內，采用LES模型模擬得到的流致振動頻率最接近試驗值，與試驗值之間的偏差在1.51%以內。

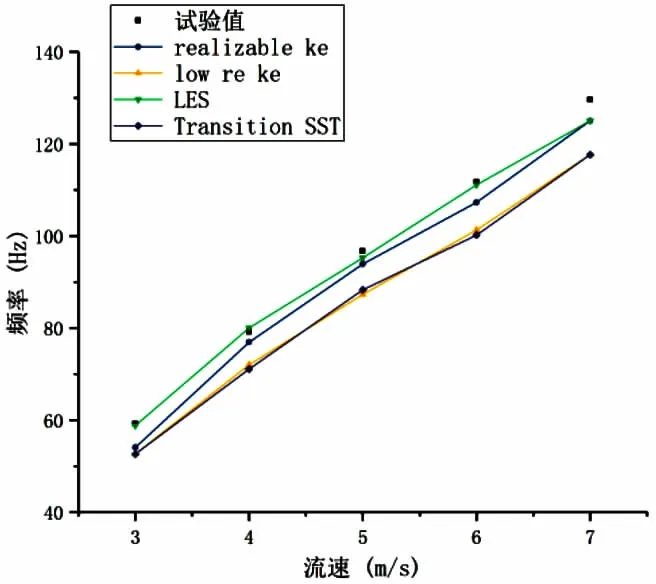
圖5 直管的流致振動頻率

4 結語

本研究采用四種不同的湍流模型，在3～7m/s流速范圍內，分別進行流體橫向沖刷直管的流固耦合計算，得到直管的流致振動特性。通過與試驗值對比分析，得出結論如下：

（1）在3～7m/s流速范圍內，在流固耦合計算中，流場的湍流模型選擇LES模型能更好地模擬直管在橫流沖刷下的流致振動，得到的x、y方向上的振幅最接近試驗值，且偏差在5%以內；

（2）在3～7m/s流速范圍內，LES模型對流致振動頻率的模擬最準確，其次為Realizable k-e模型。

本研究認為，在3～7m/s流速范圍內，LES模型能更好地模擬直管在橫流沖刷下的流致振動問題，耦合計算得到的振動幅值與試驗值之間的偏差小于5%，振動頻率與試驗值之間的偏差小于2%，但更廣范圍內的適用性，仍需進一步的驗證。

d：直管的外徑

f：直管的一階固有頻率