小樣本概率關聯度模型研究
寧小磊, 吳穎霞, 趙新, 趙軍民, 張凱, 郝跳鋒,呂梅柏, 胡亞峰, 陳韻
(1.中國華陰兵器試驗中心, 陜西 華陰 714200; 2.西安現代控制技術研究所, 陜西 西安 710065;3.西北工業大學 航天學院, 陜西 西安 710072)
關聯分析是發現、查詢數據之間關聯性或相關性的一種實用分析技術,描述了事物中某些屬性同時出現的規律和模式[1-2]。關聯分析在經濟學、軍事學、互聯網、航空航天及人工智能等領域有著廣泛應用[3-4],其中時間序列分析是數據關聯分析領域的熱點研究內容。
對不同工程背景及應用需求,目前已經提出了多種數據關聯分析方法[5-6]。文獻[1]提出了一種信息不確定條件下的時間序列關聯分析法,解決了時間序列中含有不確定信息時的數據關聯分析問題。文獻[7]提出了一種灰色關聯分析方法,解決了時間序列曲線相似性關聯分析問題。常見的時間序列關聯分析方法還有TIC法、相關系數法、誤差分析法、EARTH方法等[7],這些方法操作簡單,應用廣泛,但主要適用于單樣本時間序列之間的分析,不適合工程中經常遇到的多樣本(多元)時間序列情況[4]。針對多樣本關聯分析,文獻[4]提出了一種概率關聯度模型和概率關聯分析方法,實現了由序列曲線關聯向立體面板關聯的方法拓展,但計算時需要由比較序列樣本構建累積分布函數。實際應用中由于試驗抽樣的昂貴性、復雜性和困難性等,比較序列在實際情況中常常是小樣本數據容量,構建的累積分布函數與真實分布差別一般較大,若直接應用概率關聯度模型,關聯分析效果較差,嚴重影響了概率關聯度模型的工程應用范圍。
針對上述問題,本文提出一種小樣本概率關聯度模型。使用樣本函數或樣本統計量代替樣本構造累積經驗分布函數并計算概率關聯系數,發展了概率關聯度模型的理論框架。當比較序列樣本容量n<5時,使用樣本函數或樣本統計量構建累積分布函數計算概率關聯系數;當比較序列樣本容量n≥5時,使用Bootstrap方法重抽樣擴展樣本后構建積累分布函數計算概率關聯系數,改進了概率關聯度模型中關聯系數的計算方法,從而提高了概率關聯分析的效率。通過仿真案例和實際應用驗證了本文方法的正確性和有效性。
1 問題描述與分析
假設有參考序列x為
x=[x(1),x(2), …,x(k), …,x(T)]
(1)
比較序列y為
(2)
式中:k為時刻;T為序列長度。
參考序列x和比較序列y之間的數據關聯度為C,一般地,C可由如(3)式計算
C(x,y)=consistency(x,y)
(3)
式中:consistency(·)為一致性分析函數,也稱一致性檢驗算子,一般有C(x,y)∈[0,1]。文獻[4]總結分析了目前常見的一致性分析函數consistency(·),并提出了一種適合多樣本時間序列的概率關聯算子和概率關聯分析方法。
參考序列x和比較序列y之間的概率關聯度計算步驟如下[4]:
步驟1計算k時刻概率關聯系數poperator(k)
poperator(k)=Fy(k)(x(k))
(4)
步驟2計算概率關聯度p
p=c(poperator)
(5)
式中:Fy(k)(·)為由比較序列樣本y1∶n(k)確定的累積分布函數;Fy(k)(x(k))為x(k)在累積分布函數Fy(k)中的累積分布函數值;c(·)為概率關聯度模型中的綜合概率度計算公式,可取均勻檢驗結果。
從(4)~(5)式可見,步驟1中需要由比較序列樣本y1∶n(k)構建累積分布函數Fy(k),當比較序列y1∶n(k)樣本容量較大時(樣本量n較大時),可以構建比較精確的累積分布函數Fy(k),綜合計算得到的概率關聯度p比較符合實際。當比較序列y1∶n(k)樣本容量較小時,由比較序列y1∶n(k)構建的累積分布函數Fy(k)因抽樣誤差與實際分布函數差距較大,此時,若應用綜合計算概率關聯度p進行分析決策風險較大。工程實際中,由于試驗抽樣的昂貴性、復雜性和困難性,經常會遇到小樣本情況的比較序列數據,限制了概率關聯度模型的實際應用效果和應用范圍。
2 小樣本概率關聯度模型
2.1 改進思路
綜上可知,小樣本條件下概率關聯度模型應用遇到的主要問題是:比較序列y1∶n(k)樣本容量n有限,基于比較序列樣本y1∶n(k)不容易構建精確的累積分布函數Fy(k),導致概率關聯度模型使用效果較差。解決該問題的有效方法是使用小樣本比較序列y1∶n(k)構建滿足要求的累積分布函數Fy(k)。
Bootstrap方法是Efron于1979年提出的一種逼近復雜系統統計量估計值分布的統計方法[8],是目前被廣泛采用的小樣本數據處理方法,可以用來解決概率關聯度模型面臨的小樣本問題,即使用Bootstrap方法重抽樣擴展樣本后構建積累分布函數計算概率關聯系數。但通常Bootstrap方法樣本容量以n≥5較合適[9-10],當n<5時,其計算結果的任意性很大,構造的經驗分布函數和統計效果較差。針對樣本容量n<5的情況,文獻[3,9]使用了一種樣本順序比率統計量K,在樣本容量n<5的條件下應用效果較好[3],認為相對于樣本總體分布函數或經驗分布函數,使用樣本順序比率統計量K分布函數相容性檢驗效率更高,可見小子樣樣本構建樣本順序比率統計量K經驗分布函數比小子樣樣本構建樣本經驗分布函數精度要好。因此,可以使用樣本順序比率統計量K的經驗分布函數代替概率關聯度模型中的經驗分布函數。
2.2 變量函數概率關聯度模型改進
文獻[4]提出的概率關聯度模型,使用比較序列樣本y1∶n(k)直接構建經驗分布函數,但樣本順序比率統計量K是比較序列樣本的函數,不能直接使用。為了解決該問題,拓展概率關聯度模型的使用范圍,提出了變量函數概率關聯度改進模型,使其能同時應用于樣本或樣本函數構建經驗分布函數。
為便于描述,首先引入2個引理。
引理1設X是一連續隨機變量,其分布函數為F(X),則F(X)服從[0,1]上的均勻分布。
引理2設Y=f(X)是一連續隨機變量,其分布函數為F(f(X)),則F(f(X))服從[0,1]上的均勻分布。
從上述2個引理可見,變量或變量函數(變量統計量)均可以代人概率關聯度模型中計算概率關聯系數,因此對基本概率關聯度模型改進如下:
步驟1計算k時刻概率關聯系數poperator(k)
poperator(k)=Fy(k)(f(x(k)))
(6)
步驟2計算概率關聯度p,算子如下
p=c(poperator)
(7)
式中:f(·)為樣本函數或樣本統計量,一般為線性或非線性函數關系式,根據問題背景靈活選擇。
變量函數概率關聯度改進模型,可以采用樣本或樣本函數構建經驗分布函數,來滿足小樣本概率關聯度模型改進使用需求。
注1:通過上述改進,概率關聯度模型適應性更廣,但需要注意的是,并不是每一種樣本/變量函數f(·)都可以參與計算概率關聯系數,這是因為函數計算會引入誤差,或者說抽樣誤差會通過函數計算放大,所以選擇合適的變量函數或樣本統計量很關鍵。(雖然很難,但仍可以尋找到一些有用統計量,即樣本函數f(·),在小樣本條件下應用效果較好,比如文獻[9]找到的樣本順序比率統計量K。)
2.3 經驗分布函數構造
2.3.1 經驗分布函數
設x(1),x(2),x(3), …,x(n)為來自分布函數F的隨機樣本,其經驗分布函數Fn(x)定義為[11]
(8)
式中:I[·]為示性函數;#A為集合A中元素的個數。Fn(x)為x的右函數,共有n個跳躍點,跳躍度為1/n,即Fn(xi)-Fn(xi-1)=1/n,i=1,…,n,且有Fn(-∞)=0,Fn(+∞)=1。
2.3.2 樣本容量n<5經驗分布函數構造
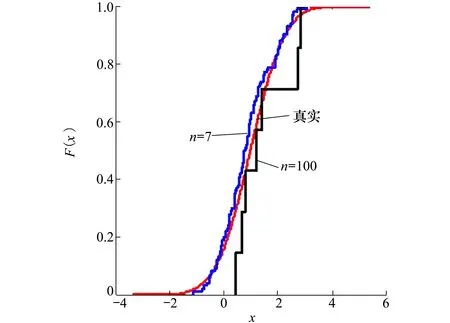
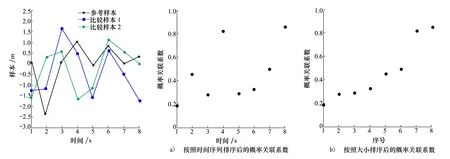
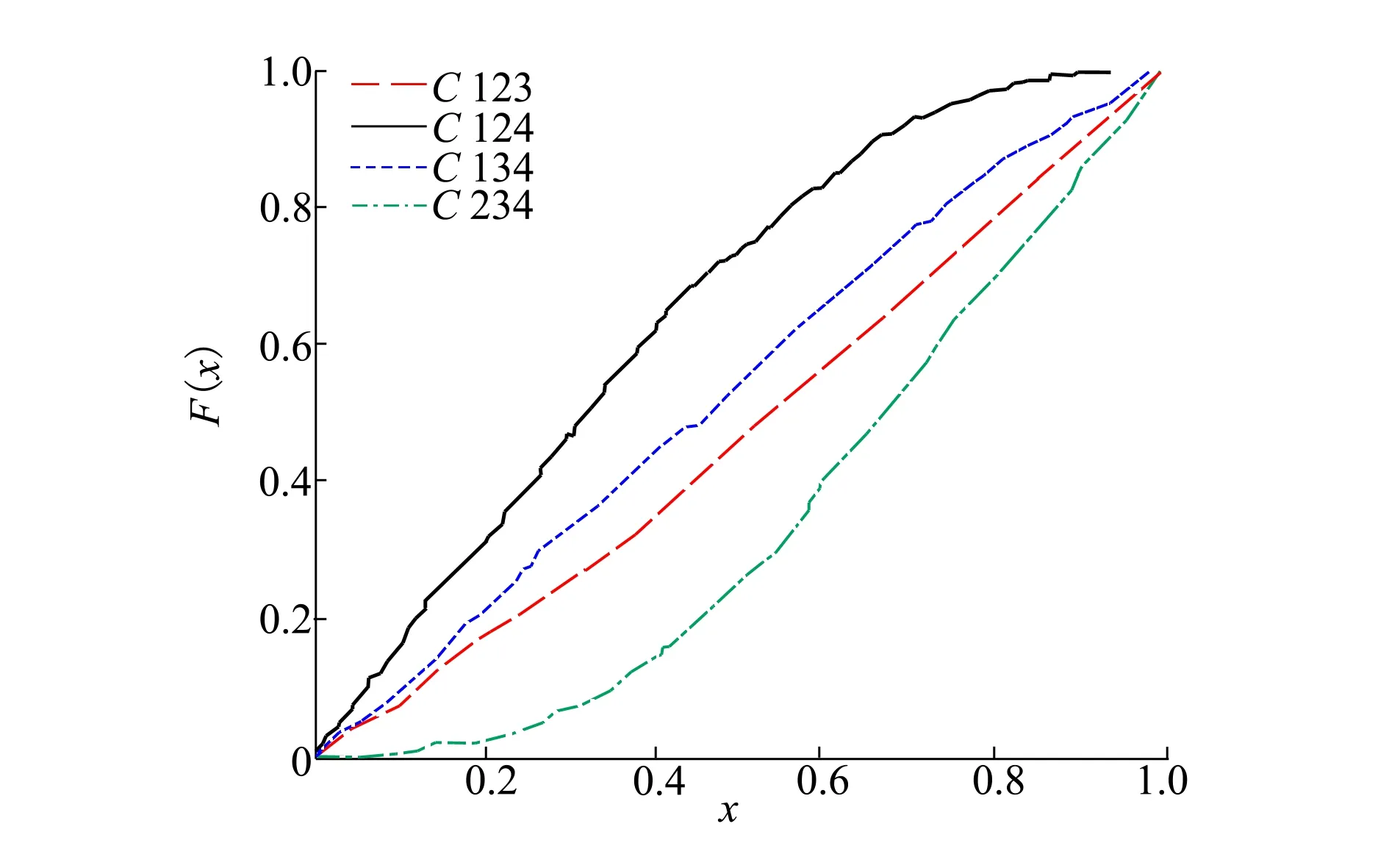
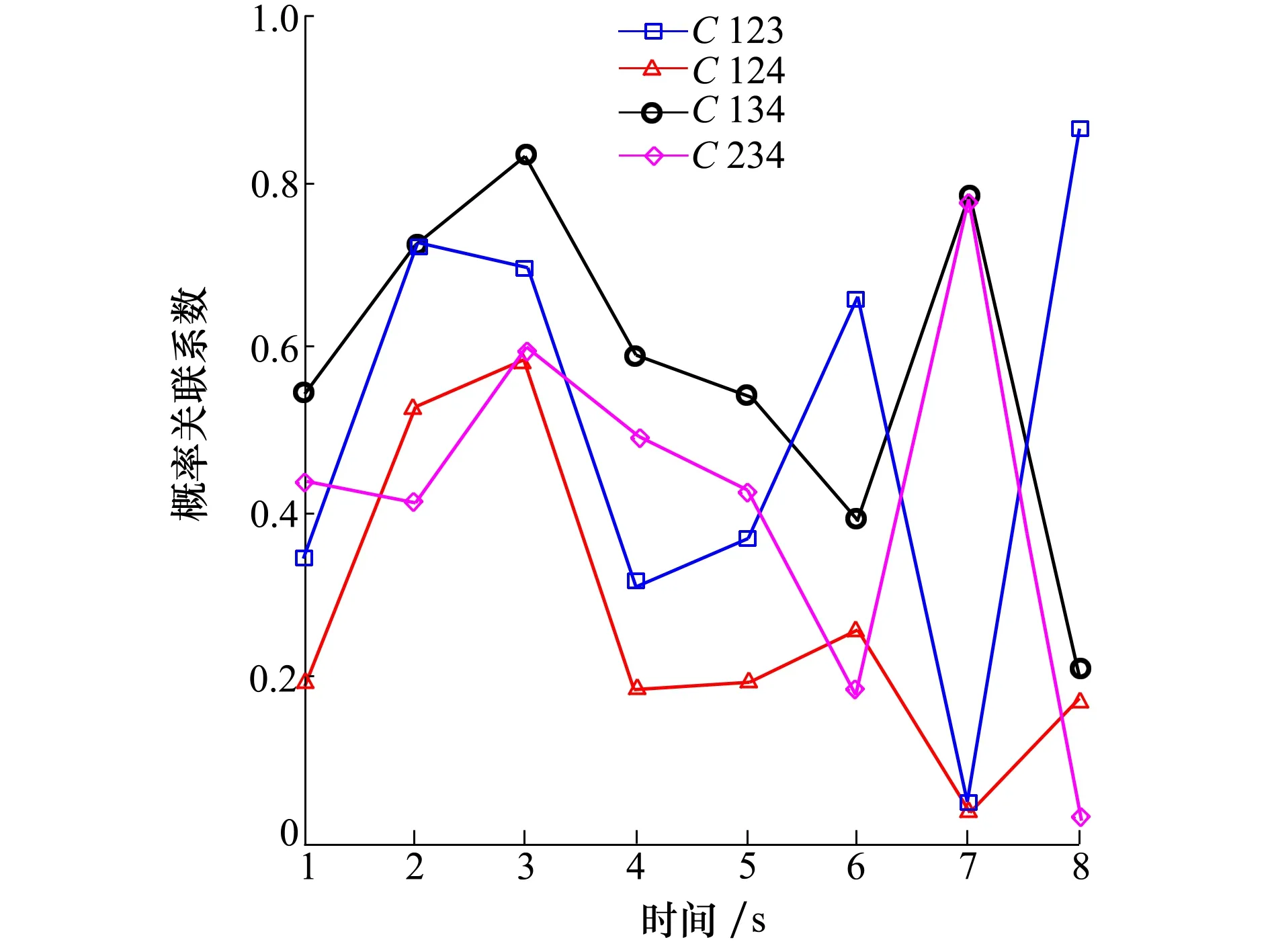
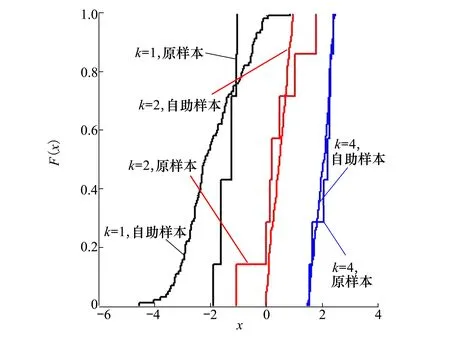
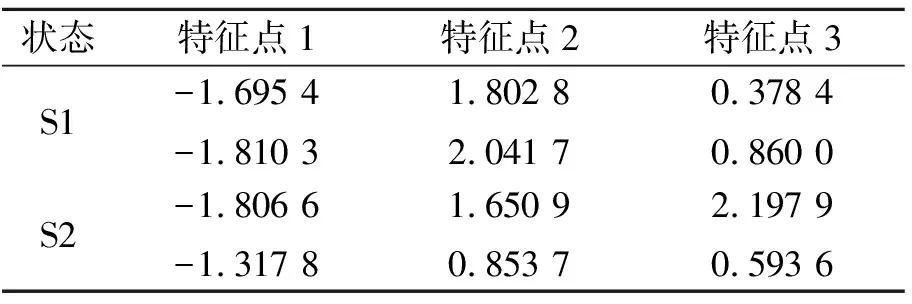
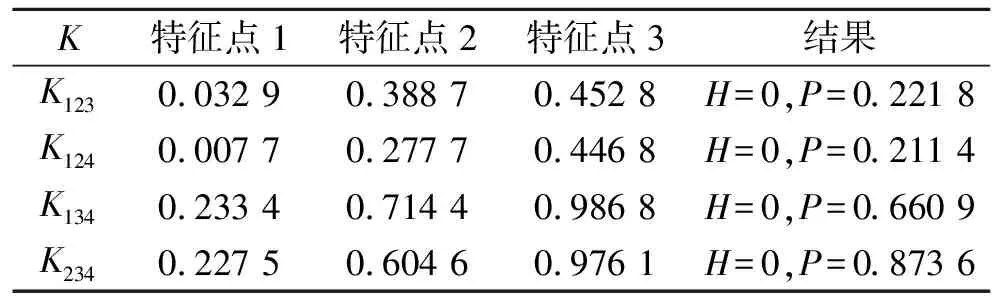
設樣本x=[x(1),x(2),x(3), …,x(n+1)](其中1個樣本模擬參考序列樣本,其他樣本模擬比較序列樣本),對樣本按自小至大順序排列,得到樣本順序統計量x′=[x(1),x(2),x(3),…,x(n+1)],則樣本順序比率統計量Kijk=(x(j)-x(i))/(x(k)-x(i)),1≤i 當n=2時,有1個統計量K123=(x(2)-x(1))/(x(3)-x(1)),且0≤K123≤1,對于樣本x來自總體X~N(μ,σ2),K123的累積分布函數為[3,9] (9) 2.3.3 樣本容量n≥5經驗分布函數構造 2.3.3.1 經典Bootstrap方法步驟 (10) (11) (12) (13) 2.3.3.2 Bootstrap方法改進 Bootstrap方法通過大量再生子樣進行統計推斷,緩解了小樣本問題,但經典的Bootstrap方法的采樣方式具有一定局限性,主要是:①樣本的累積經驗分布函數將樣本的取值范圍限制在[x(1)x(n)]中,且樣本的取值是離散的,對于連續取值的變量無法獲取樣本點之外的信息。②從公式(10)可見,當i=n或x=x(n)時,有pn=1,但理論上應是當n→∞,才有pn=1;同理x=x(1),有pn=0,但理論上應是當x→-∞,有pn=0。圖1給出不同樣本構造的經驗分布函數及真實分布函數對比。為了普適性應用概率關聯度模型,對基本Bootstrap方法進行修正,改進的主要思路是: 1) 使用樣條函數代替原經驗分布函數構造使用的階躍連接,從而解決了對于連續取值的變量無法獲取樣本點之外的信息問題。 圖1 經驗分布函數 按照以下步驟計算參考序列x和比較序列y之間的小樣本概率關聯度。 步驟1計算k時刻概率關聯系數poperator(k) (14) 步驟2計算概率關聯度p p=c(poperator) (15) 性質1小樣本概率關聯度具有以下基本性質。 1) 規范性,即0≤p(x,y)≤1; 2) 整體性,對于不同的相關因素序列xi,xj,一般有p(xi,xj)≠p(xj,xi),i≠j; 3) 可比性和唯一性; 4) 干擾因素獨立性。 性質2概率關聯度不滿足偶對稱性,即χ={x,y},有p(x,y)≠p(y,x)。 性質3概率關聯度模型不滿足數乘變換一致性和平移變換一致性。 步驟1在相同初始條件下,分別得到參考序列x和比較序列y。 (16) (17) 式中:m為參考序列x1∶m(k)樣本容量,n為比較序列y1∶n(k)樣本容量,此處可以使用矩陣型概率關聯度模型[4]。 步驟2對參考序列x和比較序列y進行預處理,使其滿足等步長、等長度的數據序列要求。 步驟3計算k時刻概率關聯系數poperator(k) 1) 當y1∶n(k)樣本容量n<5時 ①構建樣本順序比率統計量Kijk=(x(j)-x(i))/(x(k)-x(i)),1≤i ②將參考樣本x(k)帶入經驗分布函數Fy1∶n(K)計算累積分布函數值,得到關聯關聯系數poperator(k)。 2) 當y1∶n(k)樣本容量n≥5時 ②將參考樣本x(k)帶入經驗分布函數Fy1∶n(K)計算累積分布函數值,得到關聯系數poperator(k)。 步驟4決策。檢驗poperator在一定置信水平α下是否服從[0,1]上的均勻分布。若通過檢驗,說明通過關聯分析。否則,未通過概率關聯分析。 通過幾個仿真測試案例驗證本文改進模型的正確性和有效性,仿真案例分別測試樣本容量n=2(Kijk有具體理論分布解析式)、n=3(Kijk沒有具體理論分布解析式)和樣本容量n≥5時(Bootstrap方法改進)的應用場景。 仿真1參考時間序列X和比較時間序列Y為: X=[0.053 0.059-1.912 0.402 1.837-0.618 -0.043 1.125]; Y=[-0.437-2.843 0.846 0.196 0.870-0.524 1.573-0.191;-0.014-0.465-0.950-1.404 -1.257 0.447-1.328-1.241] 檢驗參考時間序列X和比較時間序列Y的一致性。 比較時間序列Y樣本容量n=2,有1個統計量K123=(x(2)-x(1))/(x(3)-x(1)), 且0≤K123≤1,累積分布函數為 (18) 圖2給出了參考時間序列和比較時間序列樣本;將參考時間序列X帶入(18)式所示累積分布函數,得到各個時刻的概率關聯系數,如圖3所示;圖3b)給出了排序后的概率關聯系數。最后計算得到的概率關聯度P=0.608 3,結果:H=0。其中,H表示仿真模型驗證結果(kstest函數的計算返回值),當H=0時,表示兩組數據一致;當H=1時,表示兩組數據不一致。 圖2 樣本序列圖3 概率關聯系數 仿真2參考時間序列X和比較時間序列Y如下: X=[0.503 1.231 1.103 0.078 0.447-0.280 -0.419-0.384-1.851-0.406]; Y=[0.607 0.337 0.119 0.311 0.623-0.824 1.801-2.039 0.029 0.745;0.333-0.352 0.356-0.914 1.588 1.765 1.429-1.196 -0.479 1.567;0.985 0.968 1.506 1.341 1.526 0.403-1.318-0.110 0.567 0.213] 檢驗參考時間序列X和比較時間序列Y的一致性。 由于比較時間序列Y樣本容量n=3時,樣本順序比率統計量K沒有顯式表達式,首先通過數值模擬的方法給出了累積概率密度分布如圖4所示。得到累積分布函數后,計算參考樣本在其中的函數值便可得到概率關聯系數。圖5給出了各個時刻的概率關聯系數。最后計算得到的概率關聯度P=0.716 1,結果:H=0。 圖4 n=3時的累積概率密度分布 圖5 概率關聯系數 仿真3參考時間序列X和比較時間序列Y如下: X=[-1.769 2.155 2.174-0.493-0.268-0.070 -0.803-0.992-1.147-1.917]; Y=[-1.241 1.583 2.739 0.508 2.029 1.004 -0.348-0.546 2.404 0.709;-1.874 2.420 2.878 0.228 0.493 0.434-1.546-0.184 -0.560 0.118;-1.233 2.319 2.485 0.025 -0.559-0.757-0.210-0.699-1.800-1.646; -1.027 2.307 2.529-1.065 1.811 0.859 1.098 0.295-0.840-0.931;-1.042 1.667 2.707 0.148-0.364 0.194-0.355-1.012 1.490-0.653;-1.619 2.085 2.432 1.055-0.943-0.559-1.386 0.343-0.475 0.568;-1.616 2.210 2.019 1.827 1.334 1.828-0.350 0.440 0.479-0.776] 檢驗參考時間序列X和比較時間序列Y的一致性。 由于k時刻比較序列Y樣本容量n≥5,首先使用Bootstrap方法重抽樣,然后基于重抽樣樣本構建累積分布函數,部分結果如圖6所示。由圖6可見,改進的自助樣本構建的累積概率分布函數明顯比由原始樣本構建的累積概率分布函數光滑。各個時刻的概率關聯系數計算結果為[0.162 0.455 0.164 0.152 0.911 0.295 0.286 0.115 0.116 0.015],最后計算得到的概率關聯度P=0.073,結果:H=1。 圖6 部分時刻累積分布函數 炮射導彈是由坦克炮發射的一種精確制導武器,提高了坦克炮的遠距離精確打擊能力。研究不同狀態下炮射導彈的彈道一致性有利于部隊訓練使用。由于炮射導彈價格的昂貴性,現場試驗組織的復雜性,現場飛行試驗樣本容量一般為小子樣。假設高原、平原2種狀態下試驗數據如表3所示,根據炮射導彈的彈道特征[13],選擇了3個典型彈道特征點(第一波谷、第一波峰、平穩點)進行一致性檢驗。 表1 試驗數據 表2 檢驗結果 檢驗結果見表2,有理由認為這2種狀態滿足彈道一致性,這與實際現場試驗結果相符。 針對小樣本條件下的數據關聯分析需求,研究提出了一種小樣本概率關聯度模型。使用樣本函數或樣本統計量的累積經驗分布函數代替由樣本構造的累積經驗分布函數,發展拓展了概率關聯度模型。當比較序列樣本容量n<5,使用樣本樣本順序統計量的經驗分布函數計算概率關聯系數;當比較序列樣本容量n≥5,使用Bootstrap方法重抽樣構造經驗分布函數計算概率關聯系數,解決了小樣本比較序列構造的累積概率分布函數誤差較大導致概率關聯系數計算不準確的問題。仿真案例和實際應用驗證了本文方法的合理性和有效性。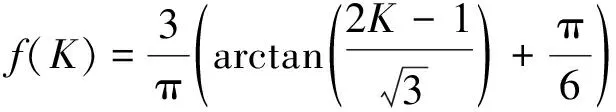
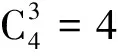
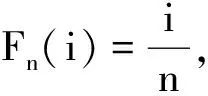
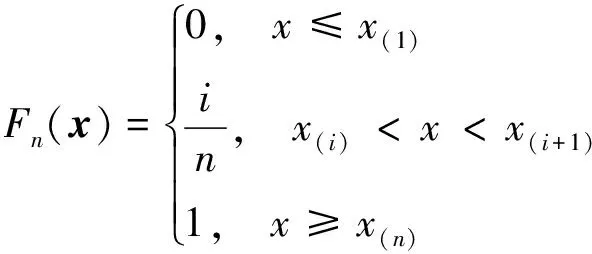
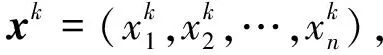
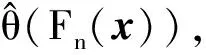
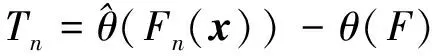
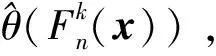
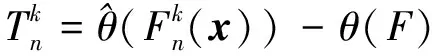
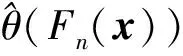
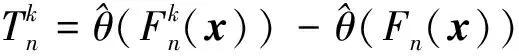
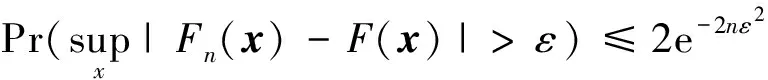
2.4 小樣本概率關聯度模型
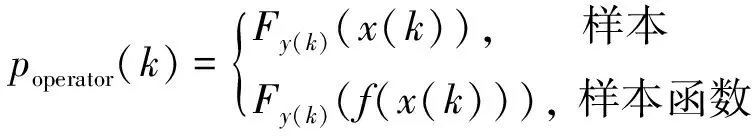
2.5 小樣本概率關聯度模型的基本性質
3 適用于小樣本問題的概率關聯分析步驟
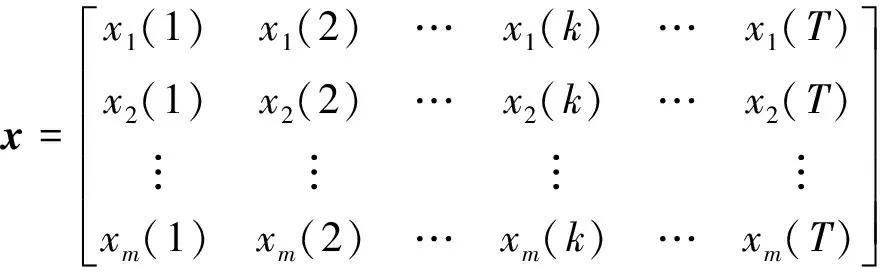
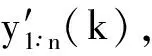
4 仿真測試與分析
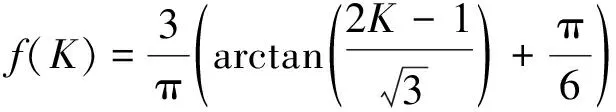
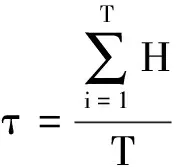
5 彈道一致性檢驗應用
6 結 論

