基于改進蜉蝣算法的水下磁場測量誤差補償

李林豐, 劉衛東, 李樂

(西北工業大學 航海學院, 陜西 西安 710072)

目前,基于三軸磁力計的航空磁探技術正逐步在水下軍事及民用領域得以應用,國內外已經開發了一系列磁場探測系統并且開展了對應的試驗。然而隨著探測距離的增加,接收到的磁性目標磁場強度大幅衰減,所以相比于航空磁場探測系統,基于水下航行器的磁場測量系統可以在距離磁性目標更近的空間進行磁場特征測量,并且可以得到更高的信噪比。因此,配置三軸磁力計的無人水下航行器(unmanned underwater vehicle,UUV)開始應用于水面磁性目標磁場特征測量[1-2]、水下磁性物質定位和跟蹤[3]以及海底磁性物理場探測[4]等任務中,這種測量方式具有很高的機動性和靈活性。

在不考慮磁力計本身誤差的情況下,三軸磁力計的測量誤差主要包括磁力計與UUV之間的安裝偏差形成的測量誤差、UUV上鐵磁性物質產生的固定磁場以及UUV航行過程中姿態發生變化時所產生的感應磁場[5]。為了提升磁力計對水下磁性目標磁場測量的精度,降低磁力計本身的安裝偏差和UUV干擾磁場對測量結果造成的影響,有必要對搭載于UUV上的三軸磁力計測量誤差的補償方法做深入研究。

在磁力計補償方法的研究中,Tolles等[6]將飛機上鐵磁性物質所產生的干擾磁場分為固定磁場、感應磁場以及渦流磁場,建立了經典的Tolles-Lawson方程。喬中坤等[7]在T-L模型的基礎上,對航磁補償技術做了進一步研究,于振濤等[8]在橢球假設理論的基礎上提出了載體干擾磁場的補償方法,這種方法需要三軸磁力計的測量軌跡擬合出一個橢球體方程,也就是說需要磁力計遍歷盡可能多的姿態角度,對于載體的要求較高。

后來的學者們根據三軸磁力計測量結果和真實地磁場值之間的關系,針對補償參數尋優算法進行了一系列研究,如使用Two-Step方法實現了搭載在微小型無人機上的三軸磁力計的補償及校準[9],這種方法具有結構簡單等優勢,但是計算過程中引入了一些中間變量,增加了補償參數求解的不確定性。Pang等[10]提出了基于最小二乘法的三軸磁力計校準,這種方法比Two-Step法具有一定的優勢,但是容易陷入局部最優。Li等[11]采用信賴域算法對補償參數進行估計,這種方法對于參數的初始值較敏感,因此在初始值選取較好的情況下可以得到不錯的補償結果。吳志添和Zhou等[12-13]分別使用總體最小二乘法(TLS)求解了補償校準參數;Liu等[14]使用奇異值分解方法完成了補償參數的估計。

由于三軸磁力計測量誤差的補償參數種類較多,估計難度高,基于上述優化算法具有一定的難度和挑戰。近些年來,隨著元啟發式算法的研究,人們發現這類算法對初始值不敏感,適合高維度的優化搜索問題,已有學者開始將啟發式算法引入磁力計的補償研究中,并且證明了這類算法相比于上述優化算法的優越性。李婷等[15]針對粒子群優化算法容易陷入局部最優的缺陷,提出了基于阻尼粒子群優化算法的磁場誤差補償,試驗結果表明相比于Two-Step,該算法的補償精度具有顯著的優勢。Zhang等[16]以某一地方的磁場強度值為常數作為約束條件,建立了地磁場的分量補償模型,并使用差分進化算法(DEA)對補償系數以及地磁場三分量進行了全局尋優,仿真結果表明該方法的補償結果要優于信賴域方法,補償后地磁場分量和總量誤差均明顯降低。Gao等[17]基于固定翼無人機的干擾磁場特征建立了磁場測量的誤差模型,推導了絕對誤差總和表達式,使用布谷鳥算法實現了補償參數的尋優,試驗結果表明布谷鳥的補償效果要優于卡爾曼濾波算法和遺傳算法。基于上述分析,國內關于載體干擾磁場的補償研究主要是針對航磁探測系統,除了補償模型外,三軸磁力計的測量精度主要受到補償參數優化算法的影響。

本文提出了基于改進蜉蝣優化算法(improved mayfly optimization algorithm,IMOA)的磁力計磁場測量誤差補償方法。首先,以課題組研制的遙控水下航行器(remotely operated vehicle,ROV)測磁系統為研究對象,分析了磁力計的安裝誤差和ROV干擾磁場,建立了磁力計的補償模型;然后,針對蜉蝣算法容易陷入局部最優以及收斂精度差的缺點進行改進,提出了IMOA方法;最后,基于IMOA方法對磁力計測量誤差的補償模型參數離線尋優,對該方法進行驗證。離線估計出來的補償參數可以應用于后續實際測量中,對磁場數據實時補償,提升ROV磁場測量系統對水下磁性目標磁場的測量精度。

1 ROV測磁系統組成

ROV測磁系統主要由一個三軸磁力計、銫光泵探頭、慣性導航模塊(INS)、數據采集模塊以及ROV運動平臺組成(見圖1)。其中,ROV主要由控制艙、能源艙、推進器、浮力模塊等組成,所有的艙體均為鋁合金材質,鋁合金的磁導率接近為1,因此艙體對磁場幾乎沒有影響,對磁場影響比較大的主要為ROV的8個推進器。

三軸磁力計和銫光泵探頭分別固定在三軸磁力計儀器艙和銫光泵探頭儀器艙內部,并且通過鋁合金測量桿固定在ROV前方不同位置處,這種結構布局減小了ROV航行時的一些隨機干擾磁場對光泵探頭和三軸磁力計2種磁場測量傳感器的影響。數據采集器和INS固定在數據采集器儀器艙內,數據采集器可以對采集到的磁場信息和姿態角信息進行濾波,數據采集模塊上安裝有SD卡用于數據存儲。

圖1 ROV磁場測量系統示意圖

2 三軸磁力計測量誤差

三軸磁力計在磁場測量過程中的誤差主要由磁力計本身相對于ROV的安裝誤差和ROV的干擾磁場形成。其中,ROV的干擾磁場主要包括硬磁誤差、軟磁誤差以及隨機干擾磁場,圖1所示ROV磁場測量系統中磁力計和ROV之間存在1 m以上的距離,因此隨機干擾磁場對于磁力計測量結果的影響可以忽略不計。

2.1 三軸磁力計安裝誤差分析

在將三軸磁力計搭載于ROV的過程中,由于安裝誤差的存在,三軸磁力計的3個測量軸無法與ROV的3個坐標軸嚴格對準,因此三軸磁力計對ROV干擾磁場的測量結果會有一定偏差,如圖2所示,其中OR-XRYRZR為ROV坐標系,Om-XmYmZm為三軸磁力計的坐標系。XR軸與ROV的縱軸方向平行,ROV航行方向為正,YR軸與ROV的橫軸方向平行,ZR軸與XRYR平面垂直,向下為正。磁力計安裝偏差的影響,會導致ORZR軸與OmZm軸之間產生夾角α,ORYR軸與OmYm軸之間產生夾角β,ORXR軸與OmXm軸之間產生夾角γ。

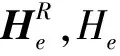
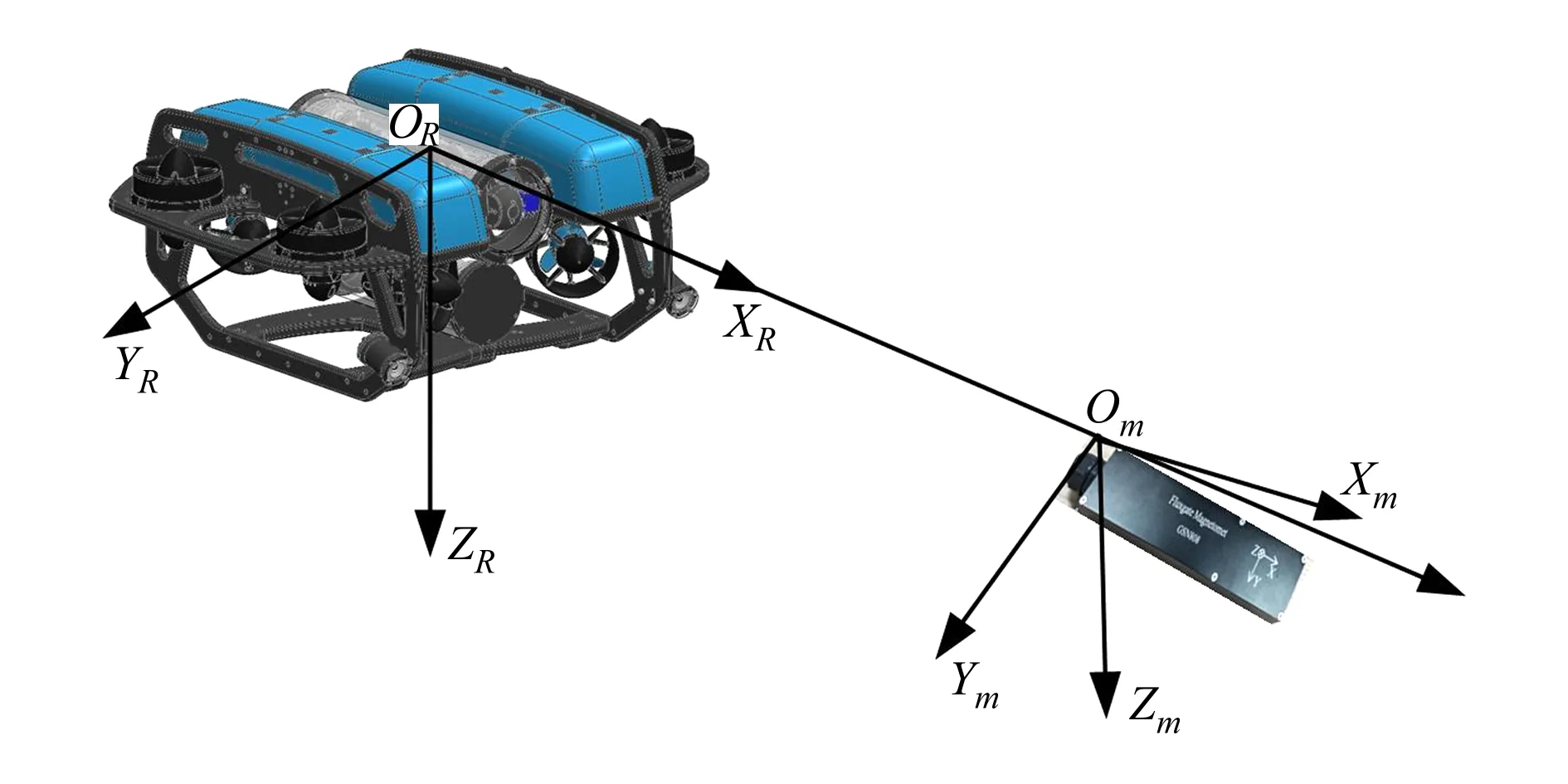
圖2 三軸磁力計相對于ROV的安裝誤差示意圖

2.2 ROV干擾磁場分析

三軸磁力計安裝在ROV上測量磁場時,由于ROV含有一些高矯頑力的硬磁性材料,這類材料經過地磁場的長期磁化以及外界載荷的作用,會產生一定的固定磁場,這種磁場在短時間內會保持相同的方向和強度,當ROV磁場測量系統組裝完成后,ROV與三軸磁力計之間的相對位姿為固定的,因此固定磁場可以表示為

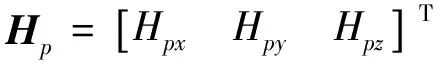
(3)

除硬磁性材料,ROV上還有高磁導率的軟磁性材料(如推進器上的硅鋼片等),ROV在航行過程中,由于洋流等外界的影響,ROV的姿態會發生不同程度的變化,從而導致軟磁性材料所產生的感應磁場發生變化,感應磁場的大小與作用在軟磁性材料上外界磁場的大小成正比,方向也由外界磁場方向決定,當ROV的姿態改變后,作用在三軸磁力計上的感應磁場也會發生相應的變化。感應磁場的表達式如公式(4)所示,其中kic為感應系數矩陣。由于感應系數矩陣的各個參數只取決于軟磁材料的磁屬性,當ROV磁場測量系統組裝完成后,ROV的材質為固定的,因此感應系數矩陣在相當長一段時間內不會發生變化。

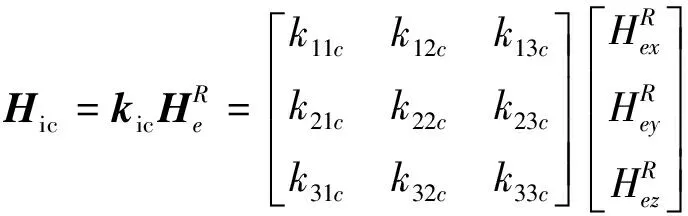
(4)

綜合(3)式和(4)式可知,ROV干擾磁場由以下兩部分組成。

HR=HP+Hic

(5)

2.3 三軸磁力計測量誤差補償模型

綜上所述,可知磁力計在水下測量地磁場過程中的輸出信號與真實地磁場信號之間有如下關系

(6)

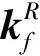
由公式(6)可以推導出磁力計坐標系下的真實地磁場表達式,如公式(7)所示。

(7)

(7)式左邊代表地磁場的實際值,右邊代表根據測量結果求解的地磁場理論值。Km可以被認為是綜合誤差系數矩陣,其表達式如(8)式所示，其中，I為3×3的單位矩陣。

(8)

對(7)式等號兩邊取模可以推導得到(9)式。

(9)

式中，f表示地磁場的真實值與理論值之差,理論上f應該等于零,從而對ROV干擾磁場的補償問題就轉化為非線性優化問題,通常在啟發式算法當中,將(10)式看作適應度函數。

minf(x)=

(10)

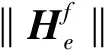
3 補償參數估計算法研究

蜉蝣優化算法(MOA)是希臘學者Konstantinos等[18-19]于2020年提出的一種仿生智能優化算法。根據優勝劣汰原則,該算法通過模仿雄性蜉蝣和雌性蜉蝣生物交配過程解決復雜優化問題。蜉蝣算法在種群更新方面可以看作是兼具了粒子群優化算法快速收斂的優點和遺傳算法“適者生存”的特性。但是,蜉蝣算法也存在容易陷入局部最優、收斂精度較差的缺陷,為此本節提出了基于Tent策略和Levy策略的改進蜉蝣優化算法(IMOA)。

3.1 原始蜉蝣算法原理

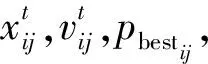
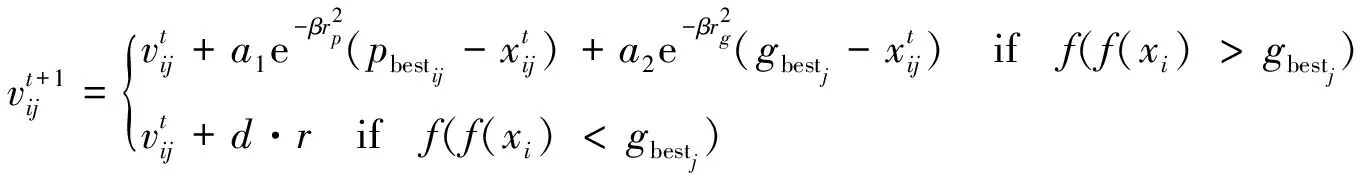
(11)

(12)

式中：a1,a2為雄性蜉蝣的吸引系數;β為能見度系數;rp代表雄性蜉蝣的當前位置與歷史最優位置之間的距離;rg代表雄性蜉蝣的當前位置與種群最優位置之間的距離;d代表舞蹈系數,用于吸引雌性蜉蝣;r為隨機系數,且r∈[-1,1]。

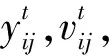
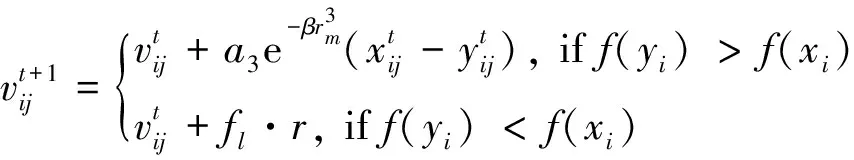
(13)

(14)

式中：a3代表雌性蜉蝣的吸引系數；rm代表雄性蜉蝣與雌性蜉蝣之間的距離；fl為隨機游走系數。

蜉蝣的交配是通過在雄性和雌性中分別隨機選取一部分樣本,雄性最優個體和雌性最優個體進行交配,次優的雄性個體和雌性個體進行交配,交配后所產生的子代通過公式(15)和(16)生成。

o1=L*m+(1-L)*f

(15)

o2=L*f+(1-L)*m

(16)

式中：o1和o2代表生成的2個子代,L為隨機數,且L∈[-1,1];m表示雄性蜉蝣;f代表雌性蜉蝣。

3.2 蜉蝣算法改進

從以下2個方面進行改進:①通過Tent混沌映射初始化蜉蝣種群,這樣不僅可以擴大種群的全局搜索范圍,還能避免種群初始化隨機性引起的算法不確定性;②采用Levy變異策略擾動部分陷入局部最優的蜉蝣個體,提升種群在迭代過程中的多樣性和抗停滯能力,使得算法可以跳出局部最優。

混沌理論是宇宙中普遍存在的一種非線性狀態,混沌變量具有隨機性、普適性,因此可以考慮將混沌理論應用于優化搜索問題中。研究表明[20],Tent映射具有優良的遍歷性和收斂速度,適合為優化搜索問題產生比較均勻的混沌序列。Tent混沌序列通過公式(17)生成。

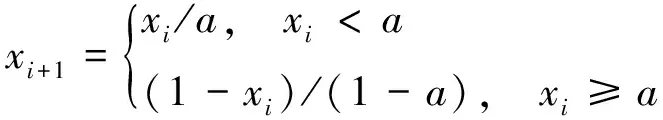
(17)

式中,a為一個隨機設置的值,且a∈[0,1],初始值x0隨機生成。

Levy變異策略來源于Levy飛行,是由法國數學家Levy提出的一種非高斯隨機過程,Levy飛行也是在自然界中普遍存在的一種現象,由于其飛行步長時大時小,因而在優化問題中可以兼顧全局優化和局部優化[21]。Levy變異的公式為

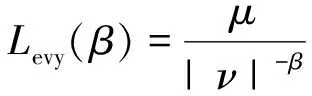
(18)

式中：β∈[0,2],μ服從N(0,σ2)分布,ν服從N(0,1)分布。

3.3 蜉蝣算法改進后計算步驟

使用改進后的MOA估計補償參數的主要步驟如下:

step1 初始化也就是生成補償參數的初始值,主要包括種群規模,目標函數的維度以及初始值的上下界,通過公式(17)生成的Tent混沌序列初始化雄性蜉蝣和雌性蜉蝣的位置,并對速度進行初始化,完成適應度函數值的初始化;

step2 開始進行迭代,首先是對雄性蜉蝣個體的更新,通過公式(11)～(12)更新位置和速度,并進行邊界處理,再更新全局最優適應度值;

step3 對雌性蜉蝣個體的更新,通過公式(13)～(14)更新位置和速度,并進行邊界處理,然后再更新全局最優適應度值;

step4 分別從更新后的雄性蜉蝣和雌性蜉蝣群體中選擇部分樣本,并且挑選出最優、次優等,根據公式(15)～(16)更新種群;

step5 根據輪盤概率,決定蜉蝣個體是否需要Levy變異,若需要變異,則按照公式(18)變異更新蜉蝣的位置;

step6 更新全局最優適應度值和最優位置。若達到最大迭代次數則結束迭代,否則轉入step2重新迭代。

4 試驗驗證

試驗地點選擇周邊沒有強磁干擾的開闊湖面,這樣測量得到的磁場僅由地磁場和ROV的干擾磁場耦合而成,有利于對本文所提出的補償參數估計算法進行驗證。在ROV的補償航行過程中,需要操控ROV在不同的航向上依次改變俯仰角和橫滾角,其變化范圍分別為±10°左右,其中慣導模塊的分辨率為0.1°,動態測量精度為0.5°。ROV航行過程如圖3所示,三軸磁力計隨著ROV的航行對當地的磁場進行持續測量。

圖3 ROV湖面補償航行示意圖

4.1 試驗過程

ROV補償航行過程中的姿態角變化如圖4所示,從圖中可以看出由于湖面水浪的作用,除了操縱ROV做出俯仰和橫滾動作外,航行過程中俯仰角和橫滾角也會發生波動。圖5為ROV航行過程中的磁場測量結果,其中圖5a)為三軸磁力計對當地磁場3個分量的測量結果,圖5b)為對三軸磁力計測量值矢量求和得到的磁場總量結果,從圖中可以看出隨著ROV姿態的變化,磁力計測量得到的3個分量具有較大的波動,其中航向角的變化對X方向和Y方向的磁場測量結果影響最大,會導致磁場測量值發生顯著的改變。計算得到的磁場總量在不同的航向上也有明顯的區別,而且磁場總量的峰峰值達到了1 540 nT,這說明了ROV的干擾磁場以及三軸磁力計的安裝誤差對磁力計測量結果的影響是不容忽視的,對于三軸磁力計的測量誤差進行補償十分必要。

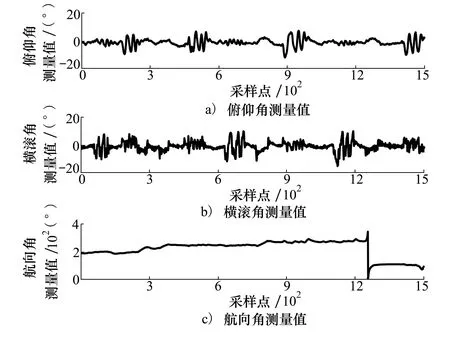
圖4 ROV補償航行過程中姿態角度測量結果

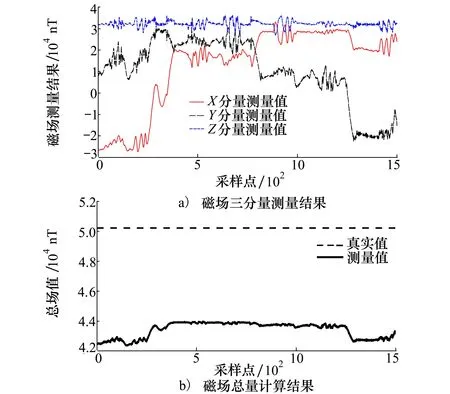
圖5 三軸磁力計磁場測量結果

4.2 試驗結果分析

在對ROV補償航行過程中測量得到的磁場信息進行補償參數估計前,首先基于ROV補償航行過程中采集到的當地經度、維度、海拔以及時間,參考國際地磁場模型(IGRF)求解出當地的背景磁場信息,作為三軸磁力計測量誤差補償的參考基準。然后,引入粒子群算法(PSOA)作為對比,在相同的條件下對本文采用的MOA和IMOA進行性能評估。

圖6為基于3種不同算法估計補償參數時適應度函數值的變化過程,可以發現在迭代前期,3種優化算法的適應度函數值均可快速下降,后期出現了平穩下降。從圖中可以發現大約經歷1 400次迭代后MOA計算達到收斂,經過800次迭代后PSOA和IMOA分別達到收斂,證明IMOA計算收斂速度要優于MOA。3種算法收斂后的適應度函數值分別為2.291×105(MOA),1.417×105(PSOA),3.926×104(IMOA),因此相對于MOA和PSOA算法,IMOA具有更好的收斂精度。

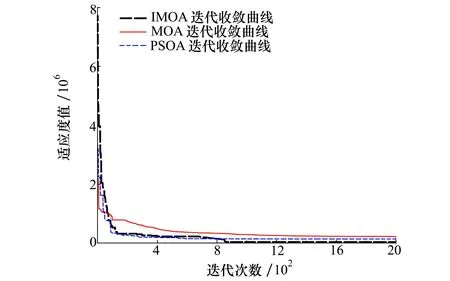
圖6 適應度函數值變化過程

分別使用3種算法估計得到的補償參數對三軸磁力計測量得到的磁場數據補償,為了便于對比3種算法的補償效果,對部分磁場測量數據補償后的誤差曲線如圖7所示,從圖中可以發現補償后的磁場誤差明顯降低。基于MOA和PSOA補償后的磁場總量及各分量誤差存在較大幅度的波動,而基于IMOA補償后的磁場總量和分量誤差分布比較均勻。

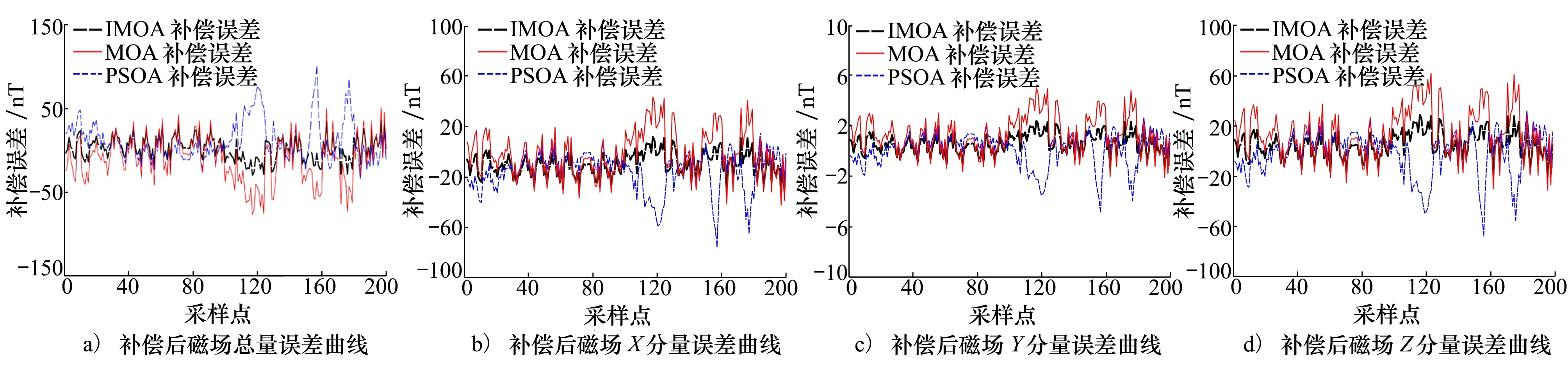
圖7 分別基于3種算法補償后的磁場誤差

為了定量地說明3種算法的補償效果,分別使用最大絕對誤差和平均絕對誤差來評估磁場的補償精度,如表1所示。

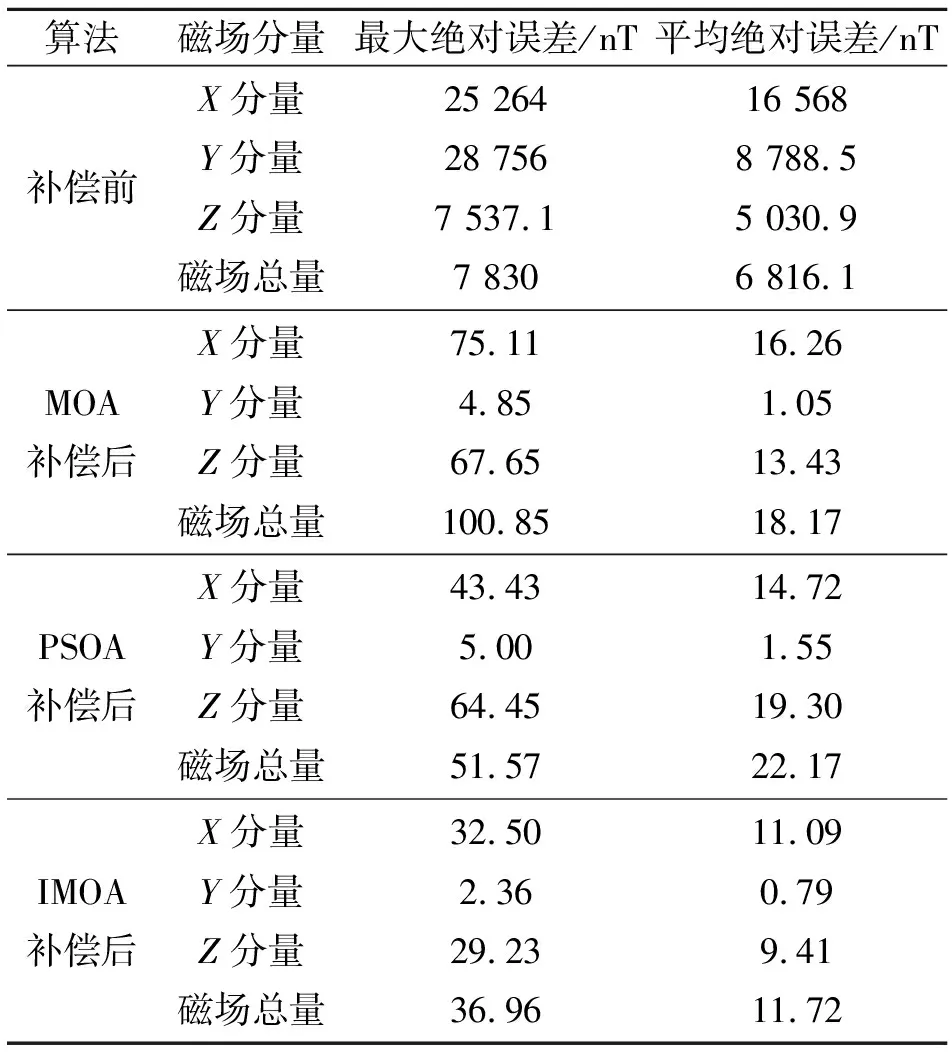
表1 補償前后磁場最大絕對誤差和平均絕對誤差

對于一組磁場數據,平均絕對誤差的表達式如(19)式所示,其中n表示磁場測量數據采樣點個數,mi表示三軸磁力計測量得到的第i組采樣點磁場值,xi表示第i組磁場數據經過補償后的結果。

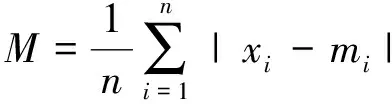
(19)

通過表1可以發現:經過補償后的地磁場總量及3個分量最大絕對誤差和平均絕對誤差都得到了顯著的降低。基于IMOA補償后,磁場的X分量、Y分量、Z分量以及總場的最大絕對誤差分別下降到真實磁場的0.58%,0.53%,0.059%以及0.55%。從表1可以看出,與基于MOA和PSOA的補償方法相比,基于IMOA的補償方法在磁場各分量和總量上具有較高的補償精度。

5 結 論

在ROV測磁系統近距離測量水面及水下磁性目標的磁場時,磁力計會受到ROV的干擾磁場等影響,導致測量結果精度難以保持穩定。針對上述問題,本文提出了一種基于改進蜉蝣算法的磁力計測量誤差補償方法。針對外場試驗中采集到的地磁場數據,分別基于MOA、PSOA和IMOA 3種方法對補償參數離線估計,并且將得到的補償參數應用到實際測量的磁場數據當中。試驗結果表明,IMOA方法能夠對磁力計的測量誤差有效補償,在相同的條件下,IMOA比MOA以及PSOA方法具有更優良的收斂速度和收斂精度。在后續的研究中,需要對IMOA的相關參數進一步尋優,此外,有必要將三軸磁力計本身的非正交誤差、零偏因子以及零漂誤差等因素考慮到補償模型當中,從而更加精確地測量水面及水下磁性目標的磁場。