函數“等值問題”變式探究
2022-11-08 09:02:50江蘇省海門中學226100
中學數學研究(江西)
2022年11期
江蘇省海門中學 (226100) 張 婕
函數“等值問題”是指“已知函數在多個自變量處的的函數值相等,這些自變量稱之為‘等值點’,求關于等值點的某個代數式的值、最值、范圍或參數的取值范圍等”的一類問題.函數“等值問題”在近年高考或各地模擬試題中高頻出現,往往處于數學試卷客觀壓軸題的位置,利用函數的圖象直觀可使問題的解決明朗化,所以也是培養和形成直觀想象數學核心素養的良好載體.
1、試題重現
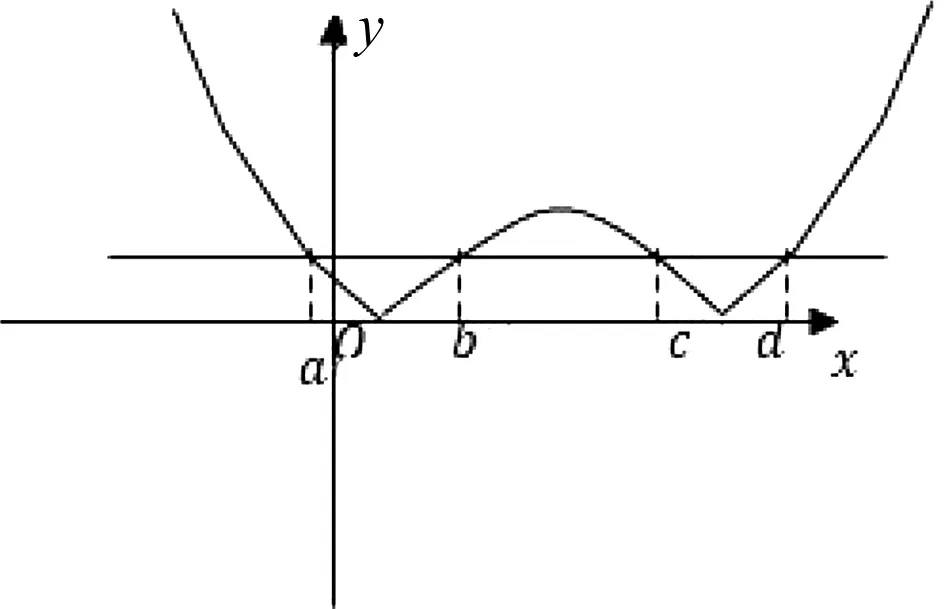
已知函數y=|x2-2x-1|的圖象與直線y=m(m∈R)有四個交點,且這四個交點的橫坐標分別為a,b,c,d滿足a 設f(x)=|x2-2x-1|,將已知條件“函數y=|x2-2x-1|的圖象與直線y=m(m∈R)有四個交點,且這四個交點的橫坐標分別為a,b,c,d”,進行轉譯為f(a)=f(b)=f(c)=f(d)=m,是典型的函數“等值問題”.作出函數y=|x2-2x-1|的圖象與直線y=m,利用函數圖象的對稱性求得a+b+c+d的值,利用求根公式用變量m表示出函數2(d-a)+(c-b),然后利用導數研究函數的單調性解得2(d-a)+(c-b)的最大值. 圖1 解:在同一直角坐標系內作出函數y=|x2-2x-1|的圖象與直線,如圖1. 函數“等值問題”是一類函數零點或方程的根等問題的延伸,借助函數圖象,數形結合解答問題,考查數學抽象、直觀想象及邏輯推理等數學核心素養在解題中的應用,多數情況下承載著高考函數客觀壓軸題的重任,比如,2020年高考數學天津卷選擇題壓軸題第9題就是一個典型例子: 求解函數“等值問題”的基本思路是:分析題意,從中挖掘出函數的奇偶性、單調性、對稱性及不變性等性質,結合函數式的特點及函數的相關性質,作出函……2、解法探析
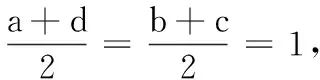

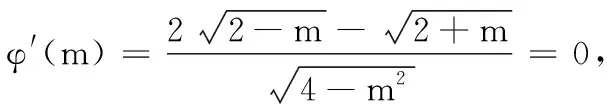
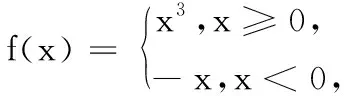
 登錄APP查看全文
登錄APP查看全文

