對一道教材例題的變式與引申*

合肥師范學院數(shù)學與統(tǒng)計學院 (230601) 李亞文 張新全

“變式教學”是我國數(shù)學教育的特色之一.由于“變式教學”的有效運用，使得我國學生在“雙基”方面的培養(yǎng)質(zhì)量得到很大的提升.筆者研究了人教版和滬科版教材中的例、習題，對課本中的一道例題進行了變式教學的探討.

1.原題再現(xiàn)

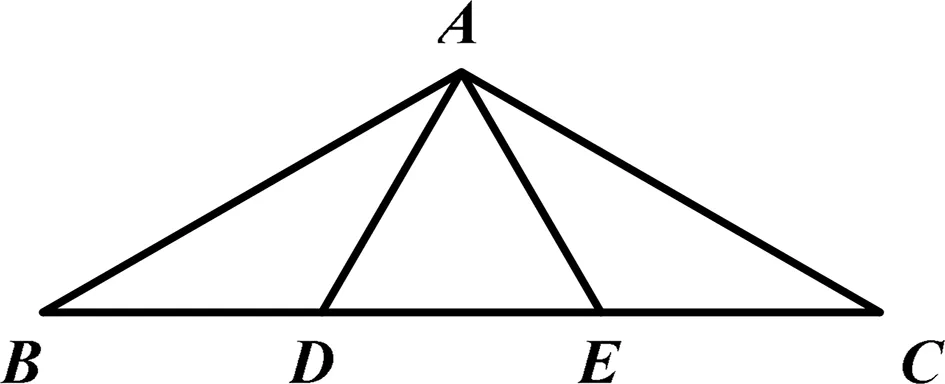
圖1

已知如圖1，在△ABC中，AB=AC,∠BAC=120°, 點D,E是底邊上兩點，且BD=AD,CE=AE.求∠DAE的度數(shù).

在人教版和滬科版教材中，該題均是“等腰三角形”這一節(jié)的例題，文[1]和文[2]對這道例題做了深入的研究，在此不作贅述，本文將變換視角，對該題進行再變式.

2.變式探究

本題涉及等腰三角形的性質(zhì)，三角形內(nèi)角與外角的關(guān)系，沿著這樣的思路，可以得到下面的變式.

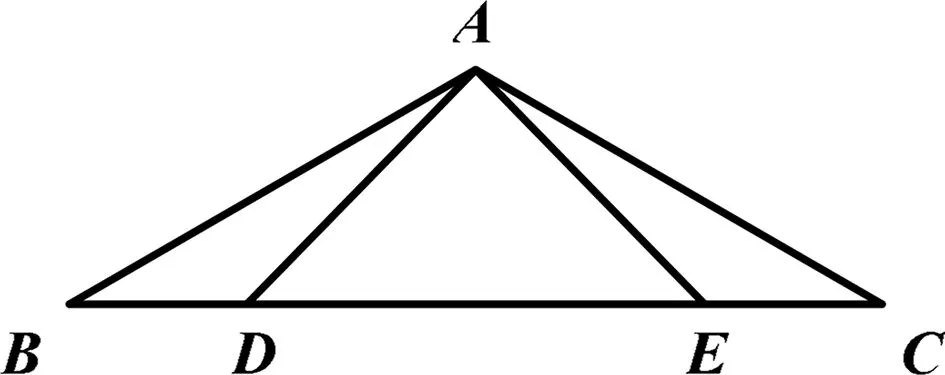
圖2

變式1 如圖2，點D,E在△ABC的邊BC上，AB=AC,AD=AE.求證：BD=CE.

這是人教版教材八年級上冊第82頁復習鞏固第6題，可以證明兩個三角形全等得到BD=CE,也可以作BC上的高，利用“三線合一”證明.

圖3

變式2 如圖3，P,Q是△ABC的邊BC上的兩點，并且BP=PQ=QC=AP=AQ，求∠BAC的度數(shù).

這是人教版教材八年級上冊第83頁拓廣探索第14題，利用等腰三角形的性質(zhì)可以求出相應(yīng)角度的度數(shù)，是例題的逆向思考.

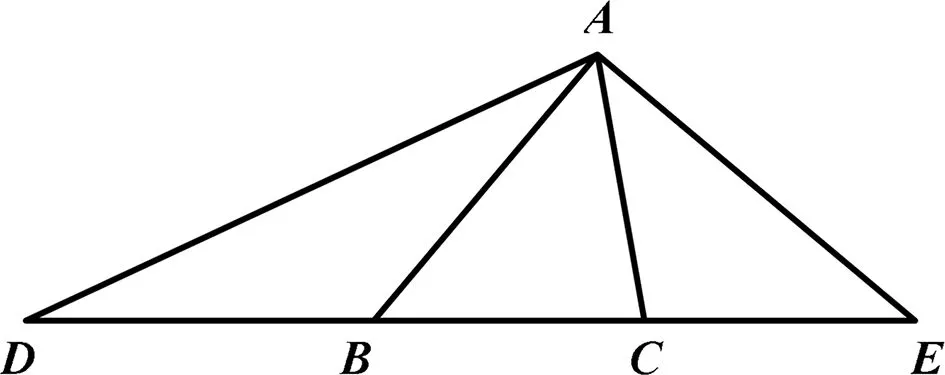
圖4

變式3 如圖4,在△ABC中，∠ABC=50°,∠ACB=80°,延長CB至D,使DB=BA,延長BC至E,使CE=CA,連接AD,AE.求∠D,∠E,∠DAE的度數(shù).

這是人教版教材八年級下冊第91頁復習題13 復習鞏固第5題，是例題的簡單綜合.這里的三個變式，都是教材上的習題，起到鞏固基礎(chǔ)知識，訓練數(shù)學思維，提升思維能力的作用，所有這些問題仍然是比較簡單的，我們還可以繼續(xù)進行變式.

變式4 在Rt△ABC中，∠BAC=90°，點D、E在BC上，且BD=BA，CE=CA，求∠DAE的角度.

對例題中相等的線段改變……