利用橢球約束求解區間平差模型的正則化方法

鄧 偉，宋迎春，李文娜，謝雪梅

(1.中南大學 地球科學與信息物理學院，長沙 410083;2.中南林業科技大學 土木工程學院，長沙 410004)

在大地測量數據處理中，隨著觀測手段的增多，觀測資料的累積，獲取先驗信息的可能性也越來越大，通過獲取的先驗信息建立約束條件一直是大地測量領域研究的熱點。傳統的最小二乘是基于殘差平方和最小的方法，但是其平差結果在一些特殊情況下并不能夠真實地表達出觀測對象的物理或者力學性質。比如將不等式約束應用到大壩變形監測中，通過坡度方向和控制點的大致移動方向建立不等式約束條件進行解算，避免在無約束平差時兩期平差值可能朝向任意方向的問題[1]。附加正確的、一定約束條件的平差模型，可以使平差結果在滿足最小二乘準則的基礎上，得到符合觀測對象規律的更合適的解。在現代大地測量領域，運用較為廣泛的就是等式約束[2-5]和不等式約束[1,6-8]，許多學者也對此進行了大量的研究并提出許多可靠的方法。

但是，在實際工程應用中，有許多用區間形式表達的參數約束信息。比如地球物理反演中的三維電阻率反演法，反演參數為電阻率，根據物理常識可以獲得電阻率范圍[9]。又如在大地測量參數反演中，反演參數巖土的密度值，由于密度是固有的正值，便能假設其大于零，且可以根據內部巖石特征得到參數值必定在某個區間內[10]。

針對參數帶區間約束的平差模型，許多學者進行了各種算法研究。謝雪梅通過將平差問題轉化為一個簡單的二次規劃問題，基于矩陣的正則分裂提出了一種迭代算法，并驗證了該算法在系數矩陣病態情況下的有效性[11]；肖兆兵將區間約束轉化為二次規劃問題，基于Kuhn-Tucker條件，針對參數的不確定度提出了一種平差迭代算法[12]。夏玉國基于積極集思想，將最優化理論中的子空間截斷牛頓法應用到測量平差中，有效改善了區間約束下平差模型的計算效率[13]。

帶區間約束條件的最優化問題，有數學學者將區間約束條件轉化成橢球約束條件進行求解[14]。即在區間約束周圍外接一個橢球，擴大約束范圍，利用橢球約束方法進行求解，將橢球特征矩陣的逆作為廣義嶺估計的嶺參數。這種方法雖然可以解決區間約束最小二乘問題，遺憾的是解有時不在區間約束內。本文借助數學上的這類方法，提出一種改進的求解橢球約束的方法，通過對橢球特征矩陣進行加權，減小特征矩陣的半徑來迭代求解，直至求出最優解。

1 區間約束最小二乘平差問題

帶有區間約束的平差模型為：

L=AX+e，權陣為P，

s.t.α≤X≤β.

(1)

式中：s.t.是subject to的縮寫，意思是“受約束”；A為m×n(m≥n)維系數矩陣;X=[x1,x2,…,xn]T為n維參數向量;L為m維線性化后觀測值與近似值之間的差值;e為n維隨機誤差向量;α=[α1,α2,…,αn]T為參數下界;β=[β1,β2,…,βn]T為參數上界。

L=AX+e,

(2)

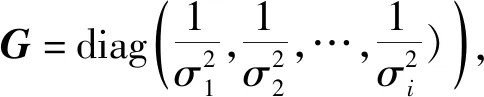
式(2)中，根據最小二乘平差準則VTPV=min，可以等價求解如下問題：

min(L-AX)TP(L-AX),

(3)

構造拉格朗日函數：

f(X)=(L-AX)TP(L-AX)+

(4)

分別對X和λ求導：

(5)

所以，

(6)

由于最優解Xλ都是在橢球面上取得，問題可以轉變為求解在橢球面上的最小二乘問題。用傳統的拉格朗日法求解式(6)的過程中，關鍵在于拉格朗日乘數λ的確定。文獻[14]中不再將λ看作一個常數，而是看作依賴于樣本的嶺參數。通過式λ=XTATPL-XTATPAX對其進行迭代求解。文獻[15]基于平衡損失函數，提出一種既考慮估計的精度，又考慮模型擬合優良程度的方法。

雖然將區間約束轉化成橢球約束可以減少約束方程，便于加入平差模型進行求解，尤其是在待估參數向量維數比較高時，但是這是一種不對等的轉換。為了便于從幾何上來分析，以二維平面上的區間約束轉換成橢球約束作為參考。如圖1可以看出，將區間約束轉化成橢球約束相當于在原本區間約束周圍外接一個橢球。如果此時再使用傳統的拉格朗日方法對橢球約束平差模型進行求解，可能會導致參數解雖然在橢球面上，但是不符合原本的區間約束條件。基于這個問題，文中提出一種新的求解橢球約束平差模型的方法，即將橢球約束條件作為一個懲罰項加入平差模型中，構造出一個新的輔助函數。懲罰項不斷加權，按照一定步長減小約束橢球的半徑，直至確定滿足原始區間約束條件的解為止。

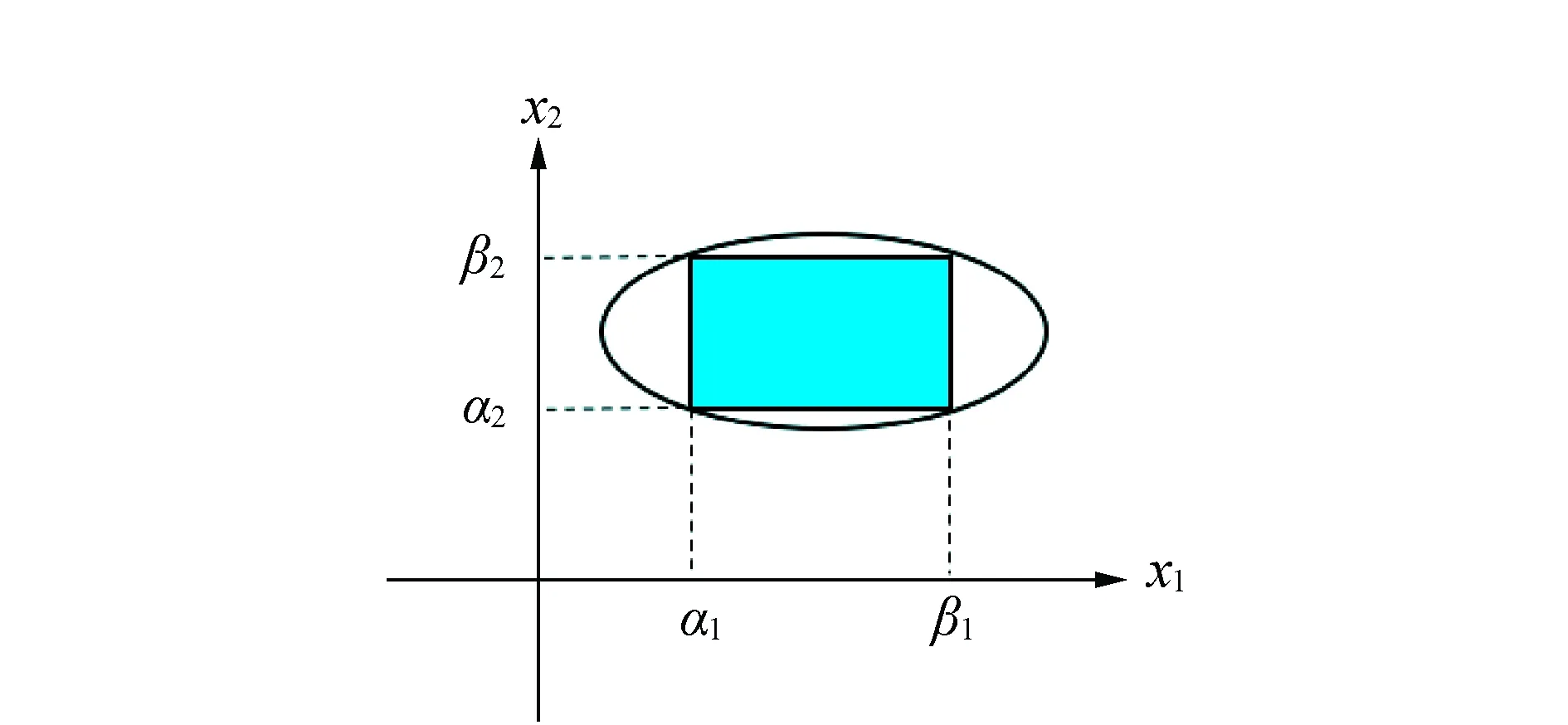
圖1 區間約束區域與橢球約束區域比較

2 二次罰函數法

二次罰函數法是罰函數法的一種特殊形式[16]，懲罰項為約束條件的平方，優點在于比較簡單、直觀。對于等式約束最小二乘問題：

minf(x) s.t.ci(x)=0.

(7)

其中f(x)為目標函數；ci(x)=0為等式約束條件，式(7)的二次懲罰函數形式為：

(8)

其中，ρ>0為懲罰因子。二次懲罰法將違反每個約束的平方的倍數加到目標函數上，在ρ→∞的過程中，對約束條件的“懲罰”就越大，可以求解出一系列的無約束解。

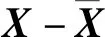
構造罰函數：

(9)

式中：μ為加權因子;Gμ為權矩陣，Gμ=μG，0≤μ≤1。通過式(9)可以看出，在μ變化的過程中，每一個橢球面上都可以求出一個在最小二乘準則下的解，但是要對該解進行判斷，判斷其是否滿足區間約束條件。μ從1開始減小，直到確定不等式(3)的解為止。

F(X)=

(10)

求F(X)關于X的一階導數并令其為0。

(11)

令二次罰函數法求得的解為：

(12)

二次罰函數法具體步驟：

1)利用先驗信息確定參數上下界α和β。

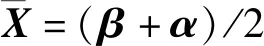
3)系數矩陣A，觀測向量L，權矩陣P，初始懲罰項Gμ，μ=1作為輸入項。

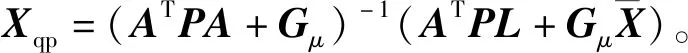
5)若對于Xqp中的所有元素，都滿足α≤Xqp≤β(即參數值在約束區間之內)，則算法終止。

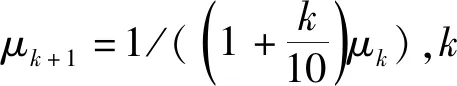
3 二次罰函數正則化

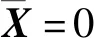
典型的正則化方法是Tikhonov正則化[17]，標準Tikhonov正則化的形式為：

(13)

式中：α為正則化參數。確定正則化參數的方法主要有L-曲線法[18]、廣義交叉核實法(Generalized Cross-Validation，GCV)[19]和嶺跡法[20]。鑒于廣義交叉核實法適用性較弱和嶺跡法選取的主觀性太強的缺點。文中選擇使用適用性強，并且能獲得較為合理的正則化參數的L-曲線法來選取正則化參數。

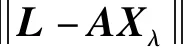
在二次罰函數法中引入正則化項，即：

minf(X)=

(14)

求f(X)關于X的一階導數并令其為0。

(15)

(16)

對于參數帶區間約束的平差模型，由于其雙邊不等式約束的特殊形式，直接求解可能比較麻煩。在計算時通常將其轉化成橢球約束進行求解，變成在橢球面上求解最小二乘解的問題。針對橢球約束會弱化不等式約束，導致解可能不在區間約束內的缺點，文中提出的二次罰函數法可以很好解決這個問題。

當系數矩陣病態時，雖然橢球約束會對模型有一定的改善，但是這種改善太依賴于參數的先驗信息。基于這樣的缺點，文中提出在二次罰函數的基礎上加入正則化項。既能通過約束條件使得最小二乘解滿足觀測對象的實際情況，又能更大限度解決系數矩陣病態帶來的解不穩定的問題。

橢球約束正則化最小二乘法步驟：

1)利用先驗信息確定參數上下界α和β。

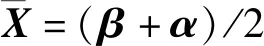
3)將系數矩陣A，觀測向量L，權矩陣P，初始懲罰項Gμ作為輸入項。

4)根據L-曲線法求出正則化參數α。

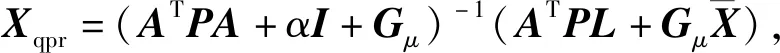
6)若對于Xqpr中的所有元素，都滿足α≤Xqpr≤β(解算出的參數值在約束區間之內)，則算法終止。

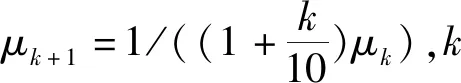
4 算例與分析

在地球物理領域常常會遇到不適定問題，例如三維電阻率反演。其正演過程是基于有限差分或有限元一類計算方法的數值解，反演則是求數量巨大的各網格剖分單元電阻率值。反演需要求取的參數是各網格單元的電阻率值，而電阻率值是可以通過物理常識確定區間范圍的，可以將約束范圍條件加入平差模型進行解算[9]。

將非線性的三維電阻率反演問題線性化后，可以得到如下的反演方程：

AΔm=Δd.

式中，A為敏感度矩陣;Δm為模型參數增量向量;Δd為觀測數據dobs與正演理論值dm的殘差向量;dm是根據給定的模型參數由數值正演得到的理論觀測值。三維電阻率反演問題往往表現為混定問題，導致方程為病態方程。

通常在模型中加入如下的不等式約束：

ρli≤mi≤ρui.

其中，mi為第i個網格的電阻率;ρli和ρui分別為第i個網格電阻率的下限和上限。對于ρli和ρui，可以根據物理常識來得到其變化的大致范圍。

綜合反演方程和不等式約束模型，可以得到如下的三維電阻率反演的目標函數：

F=min(Δd-AΔm)T(Δd-AΔm),

ρli≤mi≤ρui.

為了評價文中算法在大地測量反演中的效果，設計了如下算例進行驗證。算例中用一個希爾伯特矩陣代替三維電阻率反演中線性化后的系數矩陣，真值假設為Xzhen=[1,2,3,4,5,6]T，假設根據常識得到的電阻率反演范圍為：l=[0 0 0 0 0 0]T，u=[5 6 7 8 9 10]T，觀測值L為根據系數矩陣和真值計算出來的觀測值真值加上隨機誤差表示。A和L分別為：

L=AXzhen+e.

e為服從正態分布的隨機數組成的向量，用其來模擬測繪實際工程中的觀測誤差。為了避免數據的特殊性，采用50次數值模擬實驗，分別采取以下5種方案進行計算：

1)最小二乘法。

2)嶺估計法(嶺參數采用L-曲線法確定)。

3)奇異值分解法。

4)傳統橢球約束法。

5)二次罰函數正則化法。

令最小二乘解為Xls，嶺估計解Xre，截斷奇異值分解的解為Xsvd，傳統橢球約束的解為Xec，本文算法的解為Xqpr。

m1=(Xls-Xzhen)T(Xls-Xzhen),

m2=(Xre-Xzhen)T(Xre-Xzhen),

m3=(Xsvd-Xzhen)T(Xsvd-Xzhen),

m4=(Xec-Xzhen)T(Xec-Xzhen),

m5=(Xqpr-Xzhen)T(Xqpr-Xzhen).

m1，m2，m3，m4，m5分別代表每種方法求解出的參數偏離模擬真值的程度，結果如表1所示。

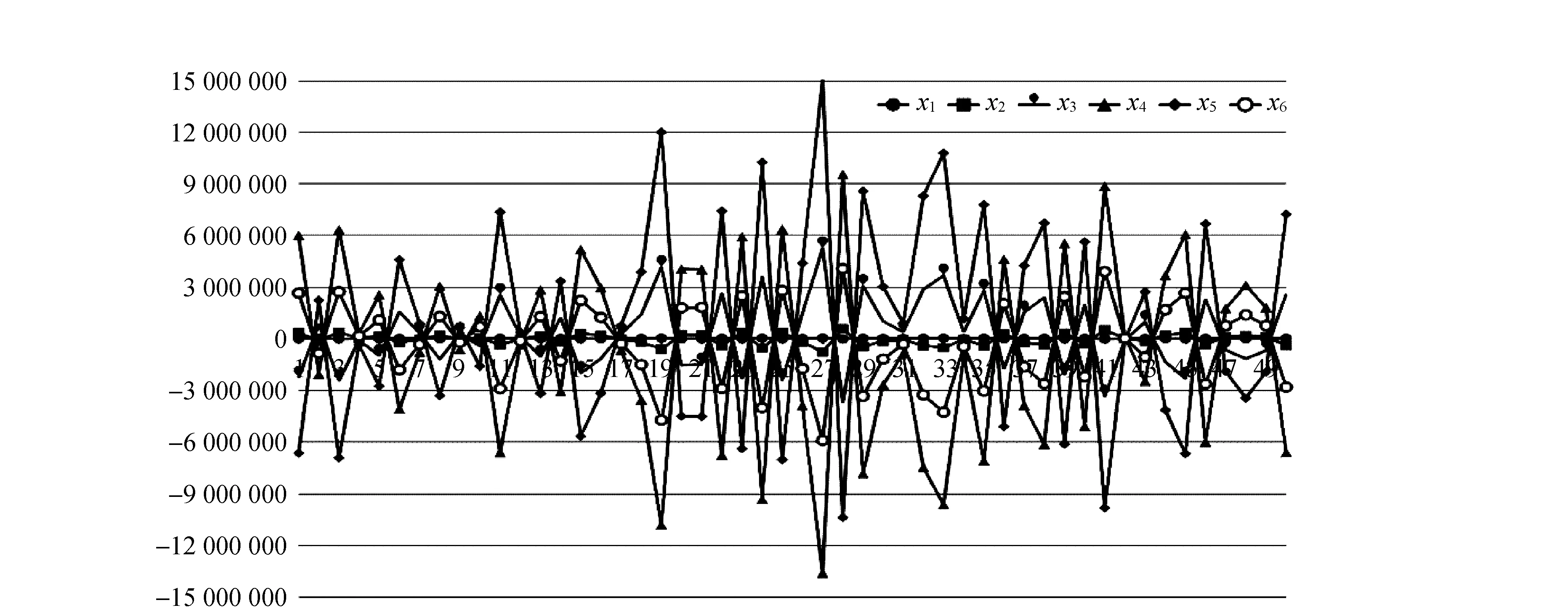
圖2 最小二乘法計算結果

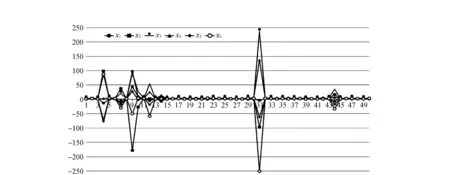
圖3 嶺估計法計算結果

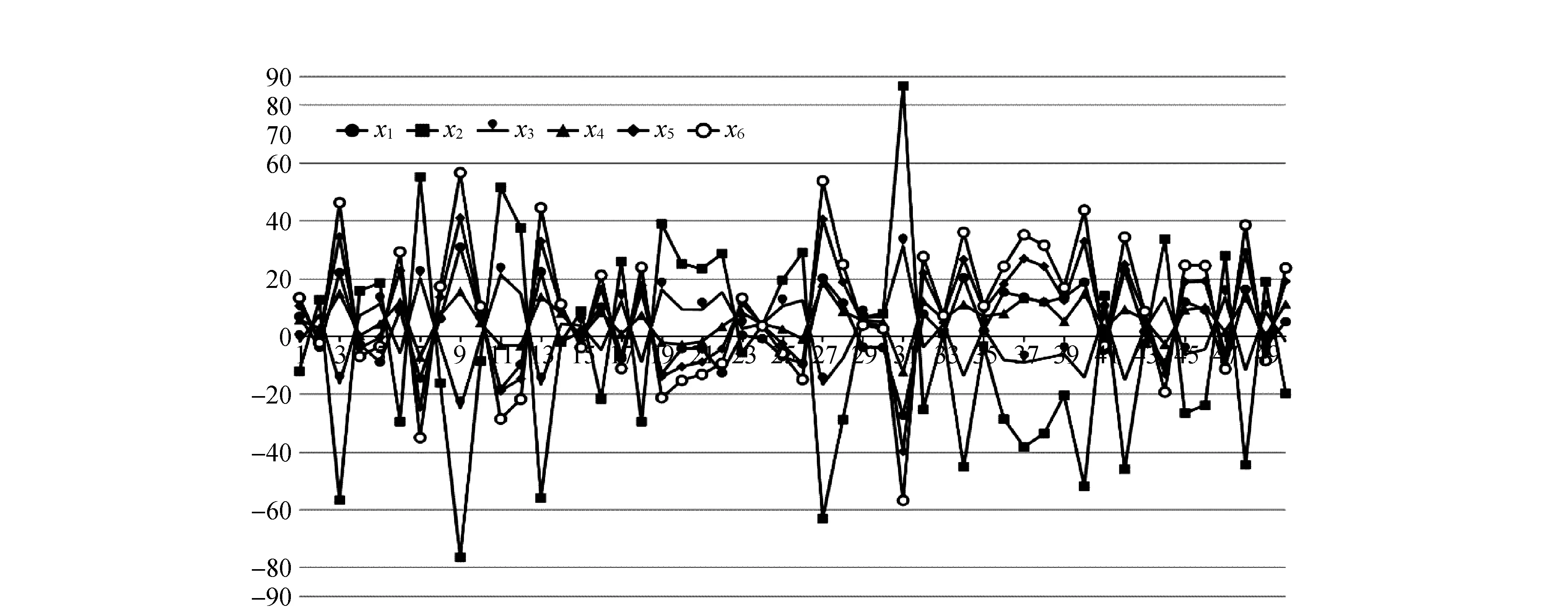
圖4 截斷奇異值分解法計算結果

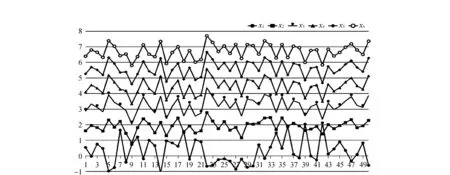
圖5 傳統橢球約束計算結果

圖6 文中算法計算結果

對模擬算例結果進行分析：

1)從表1可以看出，解偏離模擬真值的程度從大到小依次為：Xls>Xre>Xsvd>Xec>Xqpr。

2)設計矩陣A的條件數為1.495 1×108，屬于嚴重病態矩陣。從圖2可以看出，最小二乘解極不穩定，此時最小二乘解已經嚴重失真。

3) 嶺估計法對于參數的估計精度太依賴于嶺參數的選取，對模型的病態程度改善不夠理想。解的穩定性相較于最小二乘法雖然有所改善，但是其只注重于降低病態性，沒有考慮被觀測對象的實際情況。

4) 截斷奇異值分解法是通過去除設計矩陣接近于0的奇異值，通過損失待求參數的無偏性為代價來換取均方根誤差的降低。解的偏離真值程度相較于最小二乘雖有所改善，但是依然很大，且解不穩定。

5) 利用參數先驗信息，將其作為約束條件加入平差模型，可以極大提高解的穩定性。但是傳統的橢球約束算法會出現解不在約束區間里面的情況，從圖5可以看出，部分x1出現了小于0的情況。

6) 利用文中算法求出的解穩定性較好，不僅可以解決傳統橢球約束算法的解可能不在區間內的缺點，而且通過加入正則化項，可以求得正則化參數與橢球特征矩陣逆的最優組合，更好地降低模型的病態性。

5 結束語

在大地測量數據處理領域，通過在平差模型中加入有效的先驗信息作為約束條件，可以降低模型的不穩定性，提高解的精度和可靠性。文中在傳統的橢球約束解算方法上，通過引入數學領域的二次罰函數法，對橢球特征矩陣進行加權，解決了傳統橢球約束算法的解可能不在約束區間內的問題。傳統橢球約束是以橢球特征矩陣的逆為嶺參數的廣義嶺估計，文中在二次罰函數的目標函數中引入正則化項，選出正則化參數與橢球特征矩陣逆的最優組合。算例表明，文中算法在求解區間約束病態模型上有優勢。

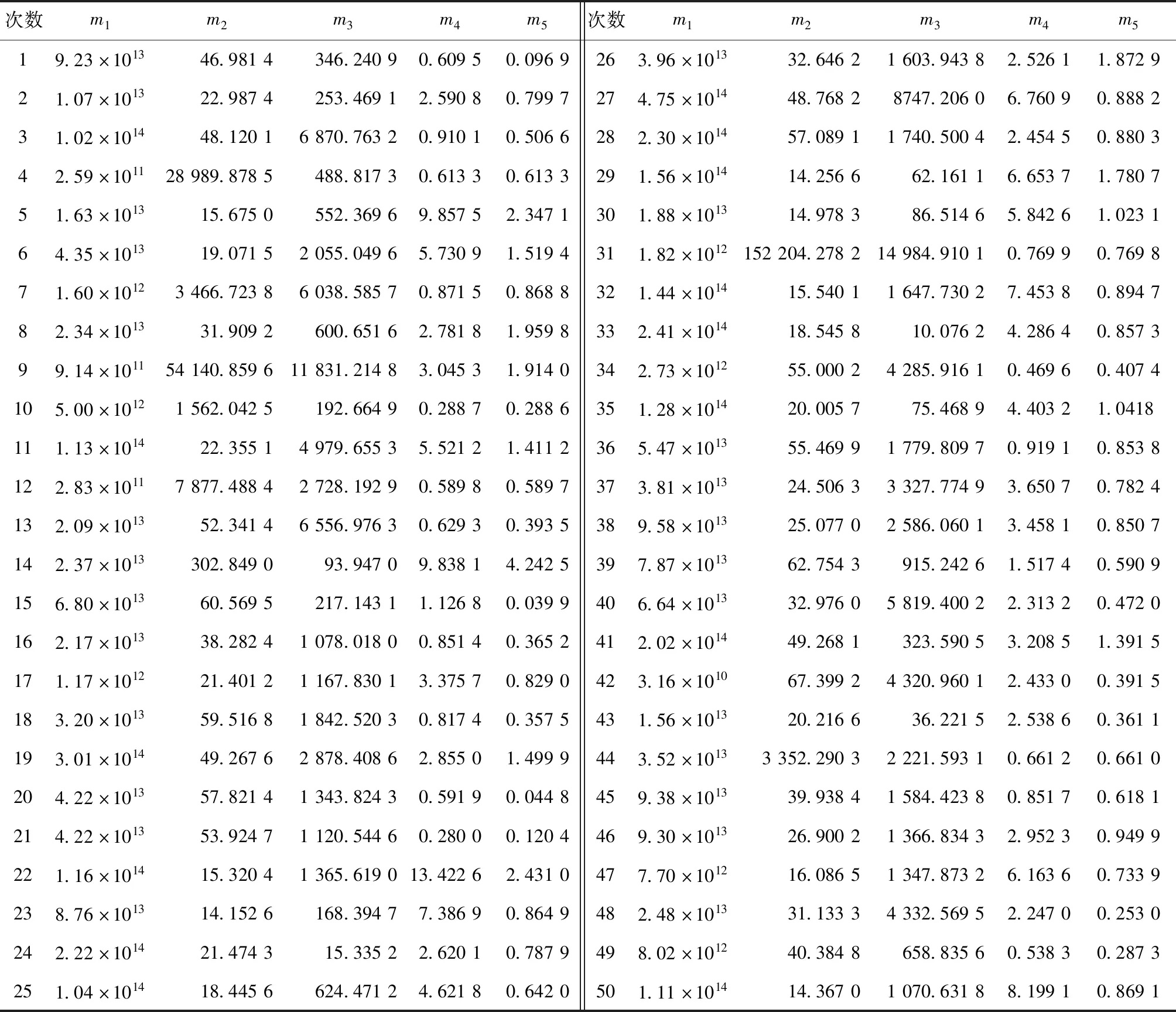
表1 解偏離真值的程度