北斗三號短基線四頻組合定位方法研究

王劍超，王志斌，李春杰，石 磊，楊海峰，張凱麗，韓 宇

(1.東南大學 交通學院，南京 211189;2.河北雄安京德高速公路有限公司，河北 霸州 065700;3.河北省交通規劃設計研究院有限公司，石家莊 050021)

當前全世界各種衛星導航系統都在不斷建設和完善，我國的北斗三號全球衛星導航系統也在2020年6月宣布組網成功，并提供多頻數據服務[1]。隨著衛星數據中的信號頻譜類型逐漸增加，多頻組合觀測是時下導航定位技術發展的熱門方向之一。研究表明，通過多頻數據的線性組合，能夠得到具有長波長、弱電離層延遲、較小觀測噪聲等優點的組合觀測值，對于提高模糊度固定效率和提升定位精度都有重要的意義[2]。

多頻觀測值組合可以改變載波波長，消減幾何方面的誤差影響，因此利于固定整周模糊度[3]。基于此，已有學者對不同情況下的多頻組合系數選擇進行了研究，并經過測試驗證了最優系數的正確性[4-5]。文獻[6]對單系統雙頻組合與雙系統單頻組合進行了分析比較，結果表明單系統雙頻組合能達到與雙系統單頻接近甚至更好的定位效果，但文章僅驗證了雙頻組合，對于更多頻的組合沒有作出進一步的分析。

目前的相關研究中，TCAR(three-frequency carrier ambiguity resolution)算法是常用的三頻觀測值組合模糊度解算方法[7-9]。傳統的TCAR算法是利用三頻觀測值線性組合，形成超寬巷、寬巷、窄巷觀測值，然后逐級固定解算模糊度的一種快速解算模糊度的方法，類似的還有CIR(cascaded integer resolution)方法，但由于第二步的寬巷模糊度難以確定，導致了該方法在模糊度解算時成功率并不理想。

在此基礎上，為了提高多頻模糊度解算效果，文獻[8]提出了一種利用北斗超寬巷輔助GPS寬巷模糊度固定的方法，利用北斗三頻組成超寬巷波長的特點幫助北斗模糊度固定，再利用北斗GPS，實現組合模式下的寬巷模糊度固定。文獻[9-10]針對目前北斗三號已提供5個頻率的數據，深入地對多頻相位模糊度固定(multi-frequency carrier ambiguity resolution,MCAR)進行了研究，結果顯示四頻數據組合可構造更多的弱電離層延遲和小觀測噪聲影響的組合觀測值，對于提高模糊度固定率有重要意義，但時下鮮有對于四頻組合定位方法的研究。

綜上所述，國內外許多學者對北斗等衛星系統多頻定位均展開了一定的研究[11-12]，同時在三頻組合方法上也早已取得了成熟的理論和實踐成果[13-16]，論證了多頻組合解算的可行性，表明了多頻觀測值組合對于模糊度固定及提升定位精度都有關鍵作用。當前三頻組合方法的研究結果都已較為成熟，但四頻及以上的多頻組合方法研究仍有很大的探索空間，在研究多頻組合理論和研究多頻模糊度解算方法的基礎上，本文提出了一種北斗四頻組合定位解算方法，并利用實測數據對該方法與北斗單頻、北斗三頻組合等方法進行了分析比較。

1 北斗三號多頻觀測值組合理論

理論上，北斗的四頻觀測數據可以隨機組合成多種不同特性的觀測量，但并不是所有的組合都可以用于定位計算，針對不同的應用場景，應選取適當的組合系數。

基于當前北斗三號的多個頻率觀測數據，通過對不同頻率的相位觀測值進行線性組合，可以獲得波長、電離層延遲等方面具有不同特點的組合觀測值。設BDS-3的4個頻段(B1C,B1I,B3I,B2a)的頻率分別為f1,f2,f3,f4，波長為λ1,λ2,λ3,λ4，系數為l,k,m,n，則以周為單位的相位觀測值組合為：

φ(l,k,m,n)=l·φ1+k·φ2+m·φ3+n·φ4.

(1)

相應地偽距組合觀測值表示為：

P(l,k,m,n)=

(2)

組合后的頻率、波長和整周模糊度為：

f(l,k,m,n)=l·f1+k·f2+m·f3+n·f4,

(3)

(4)

N(l,k,m,n)=l·N1+k·N2+m·N3+n·N4.

(5)

式中：c表示光速;N表示整周模糊度。此外，設β(k,l,m,n)和θ(k,l,m,n)分別表示一階和二階電離層延遲度因子，則可得其計算式為：

(6)

(7)

在本研究中，設各頻率的觀測值噪聲都相等且相互獨立，則對應的多頻偽距及載波相位觀測噪聲滿足：

(8)

(9)

其中，η(k,l,m,n)表示比例系數并且有：

(10)

通過不同的組合系數可以組合得到不同波長的虛擬觀測值，將不同組合按波長長短分為超寬巷(EWL，λ≥2.93)、寬巷(WL，0.75≤λ<2.93)、窄巷(NL，0.10≤λ<0.19)，對北斗三號4個頻點的數據部分組合信息進行統計，如表1所示。

表1 不同信號組合及相關信息

從表1中可以發現，不同的組合形式得到的虛擬觀測值在波長、電離層延遲以及觀測噪聲方面很難同時滿足選擇標準，因此，針對某一標準進行組合系數選擇時并不一定能夠獲得最佳的模糊度固定效果，在實際使用時需要針對實際場景進行組合系數的選取。

針對雙頻窄巷模糊度有時難以固定的問題，本文提出四頻雙窄巷組合模型，通過聯立兩個獨立不相關的雙頻窄巷觀測方程，增加多余觀測量，從而提高模糊度解算的效率和可靠性，因此，文中選取表1中的(0,1,1,0)及(1,0,0,1)兩個窄巷組合進行四頻組合定位模型的構造。

2 北斗三號四頻組合定位解算模型

2.1 北斗三號四頻組合方法

首先采用(1,0,0,1)的組合系數選取B1C和B2a頻率進行雙頻窄巷組合，設這兩個頻率的窄巷組合為NL1，則得到相應的雙差偽距和載波相位觀測方程為：

Δ?PNL1=Δ?ρ+Δ?I+Δ?T+Δ?ε,

(11)

λNL1Δ?φNL1=

Δ?ρ+λNL1Δ?NNL1-Δ?I+Δ?T+Δ?ε.

(12)

同理，采用(0,1,1,0)將另外的B1I和B3I頻率進行雙頻窄巷組合，設窄巷組合為NL2，則得到的組合方程為：

Δ?PNL2=Δ?ρ+Δ?I+Δ?T+Δ?ε,

(13)

λNL2Δ?φNL2=

Δ?ρ+λNL2Δ?NNL2-Δ?I+Δ?T+Δ?ε.

(14)

當一個歷元中有n+1顆共視衛星時，NL1雙頻窄巷組合可以分別列出n個偽距觀測方程和n個載波相位觀測方程，相應的NL2雙頻窄巷組合也可以列出n個偽距觀測方程和n個載波相位觀測方程，僅存在2n+3個未知數，聯立所有方程可以進行單歷元的解算，通過線性化可以得到誤差方程為：

(15)

其中，A矩陣為基線向量的系數陣，B矩陣為模糊度陣Δ?N的系數陣，具體為：

(16)

(17)

LL,LP分別為載波相位和偽距觀測方程的常數陣，設流動站和基準站分別為i,j，k為參考星，則常數陣具體為：

LL=

(18)

LP=

(19)

通過上述觀測模型，結合卡爾曼濾波實現模糊度浮點解的單歷元解算，同時可以獲得其協方差陣，通過LAMBDA算法即可對模糊度搜實現固定。

2.2 附有模糊度參數的卡爾曼濾波方法

根據組合觀測方程，可以得到相應的卡爾曼濾波狀態方程和觀測方程為：

(20)

各參數含義如表2所示。

表2 卡爾曼濾波方程各參數意義

在利用卡爾曼濾波解算雙差模糊度浮點解時，設某歷元觀測到的共視衛星為n，相應的就有3個坐標改正數和2n個模糊度組成待求參數，因而狀態向量和系數矩陣可設置為：

Xk=

[δX,δY,δZ,Δ?N11,Δ?N12,…，Δ?Nn1,Δ?Nn2]T,

(21)

(22)

式中：δX,δY,δZ為三維坐標改正值;Δ?Nn為待求窄巷組合雙差模糊度;Ak為坐標改正值的系數陣;λ為載波波長構成的待求雙差模糊度系數。在實際求解中，三維坐標改正值初值可設為0，根據偽距和載波的函數關系，雙差模糊度初值則可由式(23)求得。

Δ?N=(Δ?P-Δ?L)/λ.

(23)

由于初值并不夠精確，因而一般將初始狀態協方差矩陣初值設為較大值，為：

(24)

在進行靜態測量時，接收機位置不會發生變化，因此靜態測量的狀態轉移矩陣一般設為單位陣，而動態噪聲陣一般設為零矩陣。結合卡爾曼濾波的更新步驟，即可對代求參數進行估計。

需要注意的是，隨著觀測時長變長，衛星可能會發生升起或者降落，因而雙差模糊度也會發生相應的變化，因此需要設置相應的轉換矩陣，當衛星升降時對狀態向量進行轉換[9]。

3 算例分析

3.1 數據來源

本試驗數據是利用接收機在江蘇省南京市江寧區實地接收的GNSS數據，分別為長度17 m的基線SJTH-JSJN以及長度3 km的基線Coor1650-JSJN；基線SJTH-JSJN數據觀測時間為2021-1-15 UTC00:00:00—00:20:00，采樣間隔為1 s，共計 1 200個歷元的數據；基線Coor1650-JSJN數據觀測時間為2021-6-14 UTC08:00:00—14:00:00，采樣間隔為30 s，共計720個歷元的數據。兩組數據分別通過BDS單頻方法，BDS-3三頻TCAR方法和BDS-3四頻方法3種方案進行處理。

3.2 精度分析

在數據預處理后，分別通過上述3種方法進行解算，并以中海達解算軟件HGO的坐標解算結果為真值計算定位精度，結果如圖1和圖2所示。

從總體趨勢上來看，在17 m的短基線中，平面方向的解算結果比較穩定，定位誤差均在3 mm以內，高程方向解算結果波動較大，但總體定位誤差也優于6 mm；在3 km的短基線中，3種方法的解算結果定位誤差均能達到N,E方向3 mm，U方向7 mm。

為更加直觀地分析3種解算方法的相對定位精度，本文統計了兩組基線數據多種解算方式的標準差和均方根誤差值(RMSE)，分析解算結果的內符合精度和外符合精度，解算結果如圖3和圖4所示。

圖1 三種解算方式定位結果(基線SJTH-JSJN)

圖2 三種解算方式定位結果(基線Coor1650-JSJN)

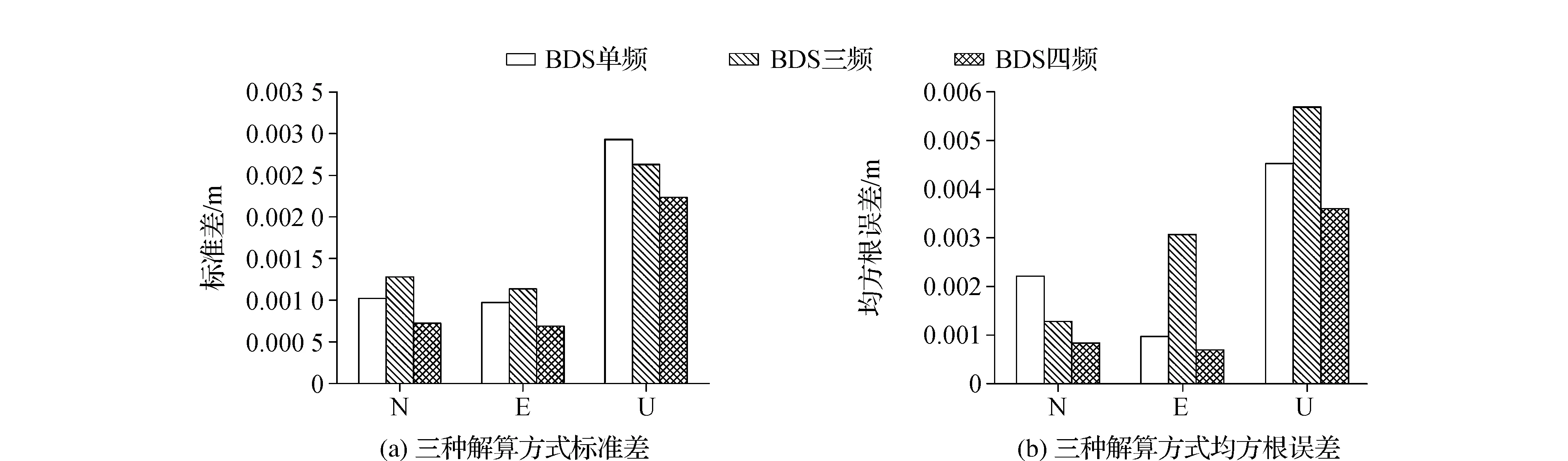
圖3 三種解算方式標準差及均方根誤差(基線SJTH-JSJN)

圖4 三種解算方式標準差及均方根誤差(基線Coor1650-JSJN)

從圖3和圖4中可以看出，在兩組試驗中，3種解算方式的標準差及均方根誤差的總體趨勢大體一致。從標準差來看，在17 m長的基線SJTH-JSJN中，3種方法在N,E方向上均在1.5 mm左右，U方向為2.5 mm左右，其中BDS-3四頻組合方法定位穩定性較好；在3 km的基線Coor1650-JSJN中，3種方法N,E方向都在2 mm以內，U方向上2.5 mm左右，其中BDS-3四頻組合方法在N,E方向上達到1.5 mm以內，U方向上達到2 mm以內，同樣體現了3種方法中BDS-3四頻組合方法的穩定性較好。

從均方根誤差來，在基線SJTH-JSJN中，3種方法在N,E方向上均小于3 mm，U方向在5 mm左右，其中BDS四頻組合解算結果最佳，平面精度優于2 mm，高程方向精度達到3.6 mm；在基線Coor1650-JSJN中，3種方法平面精度均在5 mm以內，高程方向BDS-3四頻組合方法解算結果最佳在5.5 mm，三頻TCAR方法最差在7.5 mm，實驗同樣體現了BDS-3四頻組合方法在總體精度上與其他方法精度接近甚至更佳。為了進一步體現三頻組合與其他解算方式的精度差距，統計了表3和表4。

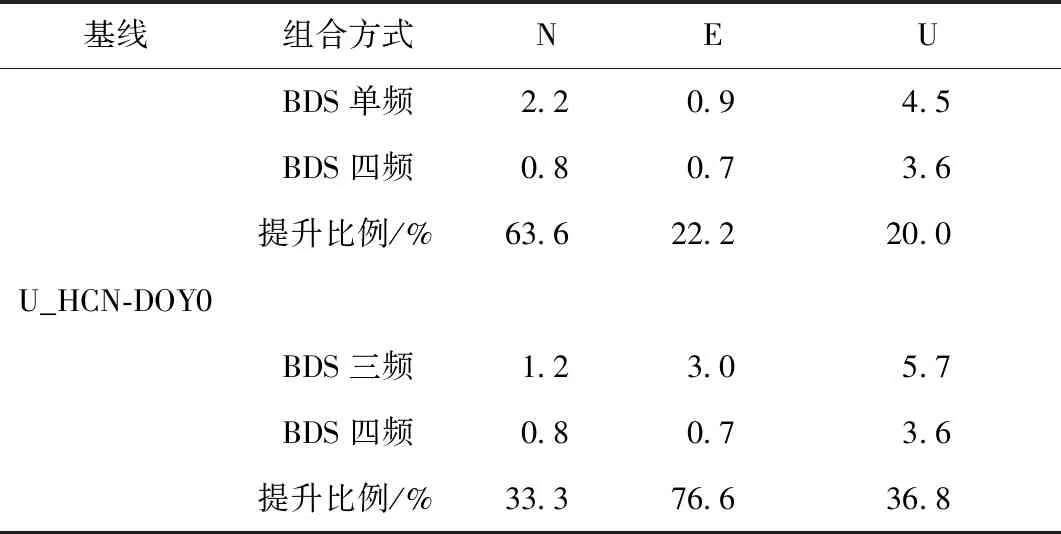
表3 SJTH-JSJN基線解算結果RMSE統計 mm

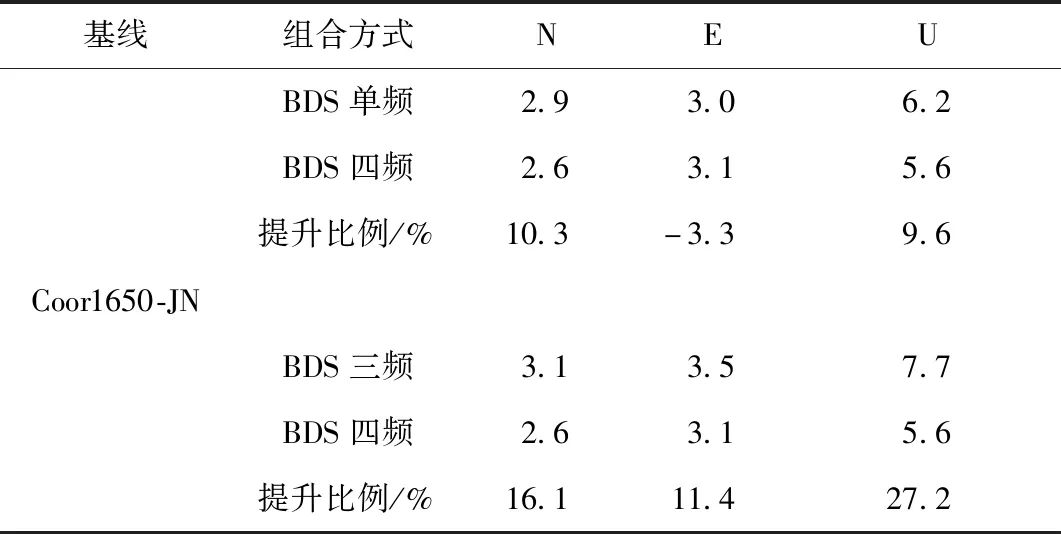
表4 Coor1650-JSJN基線解算結果RMSE統計 mm

從表3和表4中可以看出，BDS四頻組合的解算結果總體要優于另外兩種解算方法。在17 m的短基線SJTH-JSJN中，與BDS單頻方法相比，N,E,U方向分別提升了63.6%、22.2%、20.0%，相比于BDS-3三頻方法提升了33.3%、76.6%、36.8%；在3 km的短基線Coor1650-JSJN中，與BDS單頻方法相比，N,E,U方向分別提升了10.3%、-3.3%、9.6%，而相對于BDS-3三頻方法提升了16.1%、11.4%、27.2%。可以發現，在兩組試驗中BDS-3四頻組合方法總體的定位解算精度要優于其他兩種方法，因此，可以證明該四頻組合方法具有一定的可行性和可靠性。

4 結束語

本文提出了一種短基線北斗四頻組合的定位解算方法，并利用實測的數據進行試驗，比較了BDS-3四頻組合方法與BDS單頻,BDS-3三頻TCAR方法的定位精度，結果表明：

1)在17 m的短基線下，該方法平面精度優于 2 mm，高程方向精度優于4 mm；在3 km的短基線中，平面精度優于4.5 mm，高程方向精度優于6 mm。

2)綜合兩組試驗結果，該四頻組合方法相比于BDS單頻方法平面精度平均提高了35.6%，高程精度平均提高了16.1%；相比于三頻TCAR方法平面精度平均提高了46.6%，高程精度平均提高了33.2%，在本次實驗中總體定位解算效果優于單頻和三頻解算方法。

3)本文討論的方法目前僅限于短基線情況下的測試，若要進行中長基線的分析，針對對流層延遲及電離層延遲等的影響，或需建立不同的定位解算模型。同時，應增加對于該方法的試驗測試數據，建立持續分析的過程，對其性能進行多方面的評估。