多通道多分量分解方法在變轉速工況齒輪故障特征提取中的應用
張 亢 田澤宇 陳向民 廖力達 吳家騰
1.長沙理工大學能源與動力工程學院,長沙,4101142.湖南大學機械與運載工程學院,長沙,410082
0 引言
旋轉機械的振動信號包含了機械設備中零部件的健康狀態信息。對振動信號進行分析和處理是從振動信號中提取故障特征的重要手段,而故障特征是對旋轉機械進行故障狀態判斷與預測的依據[1]。齒輪是應用廣泛的旋轉機械部件,當其發生故障時,故障激勵會導致振動信號產生調制現象,使得振動信號呈現非平穩的多分量調制特征[2-3]。要提取故障特征就需要減小噪聲和其他分量的干擾,從中分離出調制成分。然而實際中,齒輪所在齒輪箱結構的復雜性以及運行工況的波動性會使傳感器測得的振動信號包含復雜的耦合成分[4],且振動信號的分量可能跨多個頻帶或同一頻帶包含多個分量,以及分量在支撐域重疊,從而造成調制成分分離困難[5]。
目前主要通過對振動信號進行分解來分離調制成分。根據信號分解實現方式的不同,現有分解方法主要可分為時域分解方法、頻域濾波分解和時頻域重構方法。經驗模態分解[6]、局域均值分解[7]、本征時間尺度分解[8]等遞歸式時域分解方法得到了大量應用,這一類方法以信號的時間尺度特征為基礎,而時頻域重疊的多分量信號在同一時間尺度上分布著多個分量,此類方法會將其識別為單個分量而無法分解;頻域濾波方法以頻帶劃分為基礎,如奇異譜分解[9]、小波包變換[10]、變分模態分解[11]等,該類方法對頻帶的劃分是機械的格型劃分,缺乏自適應性,另外對于跨多個頻帶的分量信號,會被分解到不同的頻帶之中,從而失去物理意義;時頻域重構方法通過將目標分量所在的時頻支撐域之外的時頻分布系數置零,達到分離各分量的目的,如同步壓縮變換[12-13]等。這類方法具有銳化的時頻脊線,提高了時頻的可讀性,然而當信號分量在時頻域發生交叉時,由于交叉部位擁有相同的時頻分布系數,故無法對其進行分解或錯誤分解。
根據上述分析,對于分解具有復雜時頻特征的非平穩信號,不能僅僅以信號的時頻域局部特征為基礎,而是要找到既能獨立代表分量又不受時頻特征影響的物理量作為分解的依據。最近,STANKOVIC等[14]提出了一種新的多通道多分量非平穩信號分解方法(MMD),該方法將信號中的分量用一組權重系數加權的向量線性組合表示,并以時頻聚集性度量值為優化目標,通過迭代優化得到各個分量的權重系數組,從而獲得相應的分量信號。MMD方法與前述以時頻局部特征為分解依據的分解方法相比,其本質不同在于將信號中的分量表示成一個由權重系數加權的向量,而不同的分量具有不同的系數組合,因此,理論上,對跨多個頻帶或單個頻帶中有多個分量以及分量信號發生了交叉的復雜信號也能進行分解,特別適合具有多分量調制特點且由于多激勵源耦合造成時頻分布復雜的齒輪箱振動信號的分析。目前,MMD方法僅應用于仿真信號的分析[15-16],而對于高采樣率的實際振動信號,進行時頻聚集性度量的計算量很大,從而導致MMD算法的分解時間長,實用性差。因此,要利用MMD方法分析實際振動信號,必須解決原算法中時頻聚集性度量計算量大的問題。對數窗能量準則[17]通過折中選取最佳窗長,降低時頻矩陣的規模,減少算法迭代次數,從而可間接降低時頻聚集性度量的計算量與時長。
綜上,本文在將對數窗能量準則融入MMD方法、提高MMD方法計算效率的基礎上,通過仿真信號將MMD方法與傳統的基于時間尺度的分解方法進行了對比,證明了其優勢。進一步,利用這種全新的方法,從復雜的變轉速工況齒輪箱故障振動信號中分離含有故障調制成分的分量信號,并從中提取故障特征,從而為變轉速工況齒輪故障特征提取提供了一條新的途徑。
1 MMD方法
對于任意一組多通道多分量信號x(n),MMD方法將x(n)中的每一個分量信號看作若干個特征向量的線性組合,通過優化迭代獲得該線性組合的權重系數,便可得到x(n)相應的分量信號,其具體步驟如下:
(1)將x(n)寫成
(1)
其中,x(m)(n)(m=1,2,…,S)代表第m個通道信號(即傳感器測得的數據),每一個通道信號實際上都是一組多分量信號;xp(n)=Ap(n)ejφp(n)(p=1,2,…,P)表示第p個分量成分(即系統產生的源信號),Ap(n)和φp(n)分別為瞬時幅值和瞬時相位;αmp和φmp分別為源信號經傳感器改變的幅值和相位。通過式(1)可以看出任意一個傳感器信號可以由源信號分量的線性組合來表示。
將式(1)進一步寫成矩陣形式:
Xsen=AXcom
(2)
其中,xp(p=1,2,…,P)表示分量信號xp(n)的向量形式。傳感器信號矩陣為
Xsen=[x(1)(n)x(2)(n) …x(S)(n)]T
系統產生的分量信號矩陣為
Xcom=[x1(n)x2(n) …xP(n)]T=
[x1x2…xP]T
常系數轉換矩陣為
將系統產生的信號分量轉換為傳感器測得的信號。
(2)計算Xsen的自相關矩陣R:
(3)
其中,(·)H表示矩陣的Hermitian轉置,自相關矩陣R為一個方陣。
(3)對自相關矩陣R進行特征值分解:
(4)
其中,矩陣U為特征向量矩陣;Λ為特征值對角陣;λp為特征值;up為對應的特征向量。由式(3)和式(4)可以看出,特征向量up可以用傳感器信號的線性組合表示,由上文已知傳感器信號是源信號分量的線性組合,從而可以將特征向量up用源信號分量的線性組合表示,即
(5)
當S≥P時,由式(5)可以知道,每個分量信號xp同樣可以由特征向量的線性組合表示,即
xp=η1pu1+η2pu2+…+ηPpuP
(6)
其中,ηip(i=1,2,…,P)為未知的權重系數。
(4)因為不同信號成分在時頻面上的時頻聚集性不同,所以可以用時頻聚集性來判斷信號成分。信號在時頻域的支撐區間的面積可以定量描述信號的時頻聚集性。設每個分量信號xp在時頻域的支撐區間為DTp,其面積為Dp,如果分量有重疊,那么其支撐區間必然也會重疊,但實際中支撐區間一般不會完全重疊,因此不失一般性,假設D1≤D2≤…≤DP。信號時頻分布的Lq范數可用來表示信號在時頻面上支撐區間的面積,即Lq范數可以作為聚集性測度值M{·}來度量信號的時頻聚集性,即
(7)
其中TFR(n,k)表示信號的時頻分布。因為短時傅里葉變換(short time Fourier transform,STFT)具有計算簡單、不會產生交叉項干擾等優點,且得到了成熟應用,因此,本文將STFT作為信號的時頻表示。
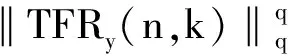
(8)
i=1,2,…,P
那么將此時的權重系數ηi1代入式(6),便可得到第一個分量信號x1。
式(8)實際上是一個優化問題,即以y的時頻聚集性測度最小為優化目標,在保證‖y‖2恒定的情況下,利用具體的優化算法計算相應的未知權重系數ηi1。本文采用遺傳算法來求解該優化問題。
(6)由式(6)可知,x1=η11u1+η21u2+…+ηP1uP,將第一個分量信號x1替換為第一個特征向量u1,然后將u1(即x1)從剩余的特征向量uk(k=2,3,…,P)中去除,即
(9)
此時得到了一組新的特征向量us(s=1,2,…,P),形成新的線性組合y=β1u1+β2u2+…+βPuP;對y重復步驟(5),可得到第二小的支撐區間面積D2對應的權重系數ηi2(i=1,2,…,P),將ηi2代入式(6)即可得到第二個分量信號x2;將x2替換特征向量u2,并從剩余的特征向量uk(k=3,4,…,P)中去除,依此類推,整個過程是一個迭代優化的過程,直到沒有新的特征向量us產生,代表信號中所有的分量xp(p=1,2,…,P)被分解出來,此時迭代終止。
從上述分解過程可以看出,每一個分量信號都是不同權重系數加權的特征向量的線性組合,其中特征向量來自于信號自身構成的矩陣,即整個分解過程是不需要先驗知識的,而表示每個分量的特征向量的線性組合是唯一的,這確保了得到的分量信號是不重復的;此外,以時頻聚集性測度最小為優化目標,通過迭代優化獲得權重系數,這保證了每一個特征向量的線性組合只對應了一個單分量信號,而不是交叉分量或組合分量等虛假分量。
2 時頻聚集性度量與仿真信號分析
2.1 基于對數窗能量準則的時頻聚集性度量
在MMD方法中,一方面,時頻聚集性度量的準確性決定了分解的效果;另一方面,以信號時頻矩陣的范數值作為時頻聚集性度量值,時頻矩陣的規模會影響算法的計算量。而對于實際振動信號,因為其較高的采樣頻率會導致大維數的時頻矩陣,所以會有很大的計算量。因此,如何保證時頻聚集性度量準確的前提下又具有小的計算量,是MMD方法應用于實際振動信號分析的關鍵。
良好的時頻分辨率是時頻聚集性度量準確的前提[18],STFT的時頻分辨率與窗長N和采樣頻率fs密切相關。對于實測振動信號,采樣頻率fs是預先設定的,窗長N決定了時頻分辨率。本文通過對數窗能量準則Q(N)來自適應確定最優窗長:
(10)
其中,G(n,k)為信號的STFT時頻分布;lgE(N)為窗能量E(N)的對數值;Mw為窗函數個數。因此,Q(N)實際上為信號STFT時頻能量與窗函數能量的對數的比值。隨著窗長N的增大,式(10)中分子分母增長速度的快慢不同,那么理論上Q(N)會在某些窗長發生折中,而當Q(N)在某個折中位置為最小值時,意味著STFT的時頻聚集性在窗長范圍內最優,那么此時對應的窗長N為最佳窗長[17-18]。
2.2 仿真信號分析
仿真信號s(t)如下:
(11)
它由3個分量組成,其中調幅分量s1(t)與線調頻分量s2(t)在時頻域發生了交叉,s3(t)為跨時頻尺度的調制分量。
首先通過對數窗能量準則確定最優窗長,為考察準則的魯棒性,設置采樣頻率分別為800 Hz、1000 Hz和1200 Hz,窗函數選用Hanning窗,窗長范圍設定為8~256。根據式(10)計算不同采樣頻率下的對數窗能量準則曲線,如圖1所示,可以看出,800 Hz、1000 Hz、1200 Hz采樣頻率下的最優窗長分別為95、119和137。
根據最優窗長對s(t)進行STFT,同時在相同采樣頻率下,選擇一個較小和一個較大的窗長進行對比,結果如圖2所示。可以明顯看出,在不同采樣頻率下,都是根據最優窗長進行STFT時獲得的時頻效果最佳;另外,在采樣頻率為1000 Hz的情況下,分別選擇不同窗長,在同一臺計算機上針對仿真信號將MMD算法各運行了30次。統計循環迭代次數和平均計算時間兩個指標,如表1所示。可以看出,相比于其他窗長,當采用對數窗能量準則確定的窗長119時,MMD算法的平均運行時間最短,迭代次數最少,說明了引入對數窗能量準則的必要性。
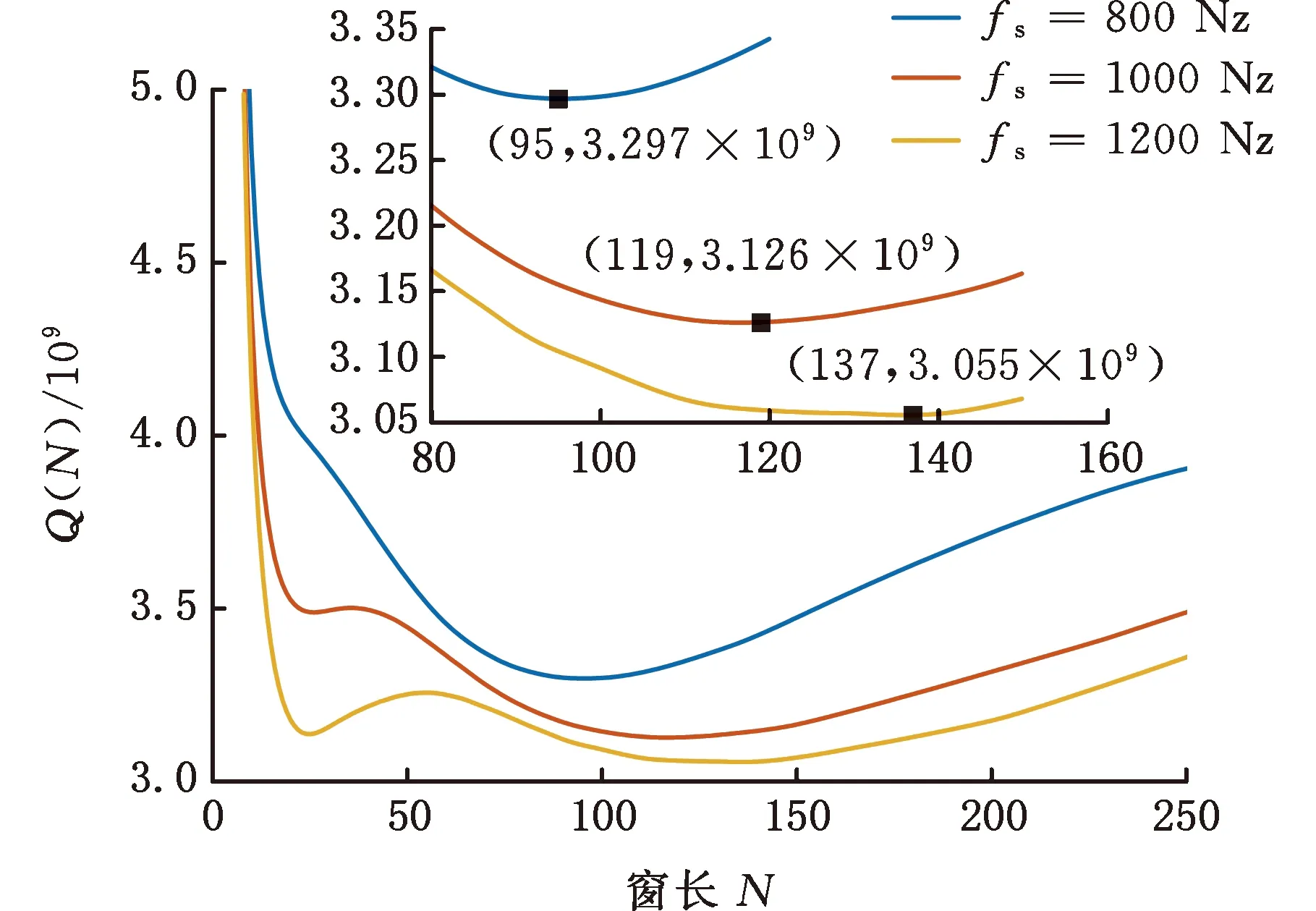
圖1 s(t)在不同采樣頻率下的對數窗能量準則曲線Fig.1 Logarithm window energy rule curve of s(t) atdifferent sampling frequencies
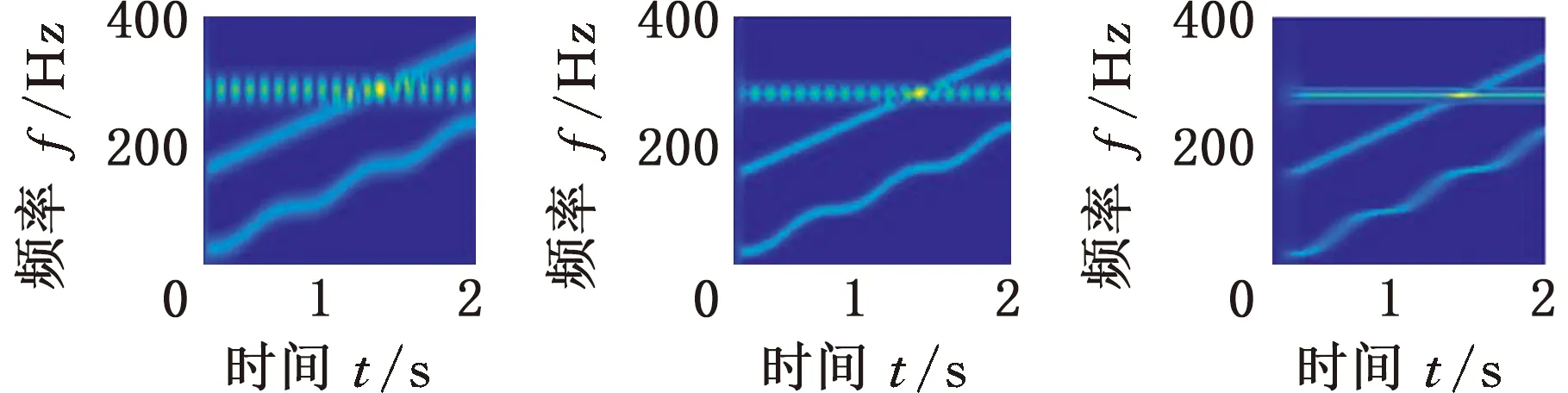
(a)fs=800 Hz,N=50 (b)fs=800 Hz,N=95 (c)fs=800 Hz,N=180
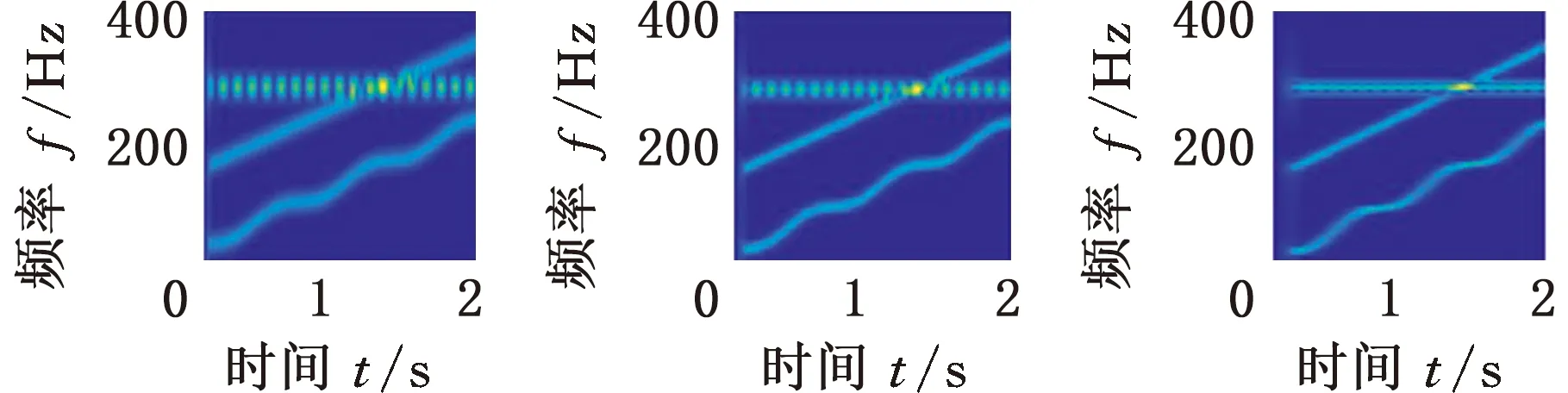
(d)fs=1000 Hz,N=95 (e)fs=1000 Hz,N=119 (f)fs=1000 Hz,N=209
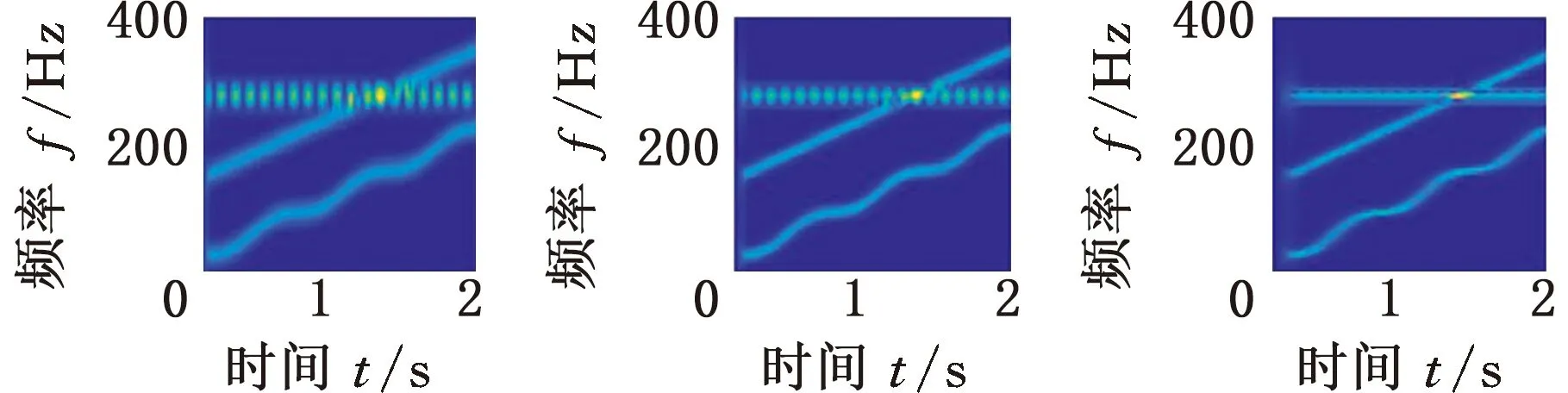
(g)fs=1200 Hz,N=119 (h)fs=1200 Hz,N=137 (i)fs=1200 Hz,N=210
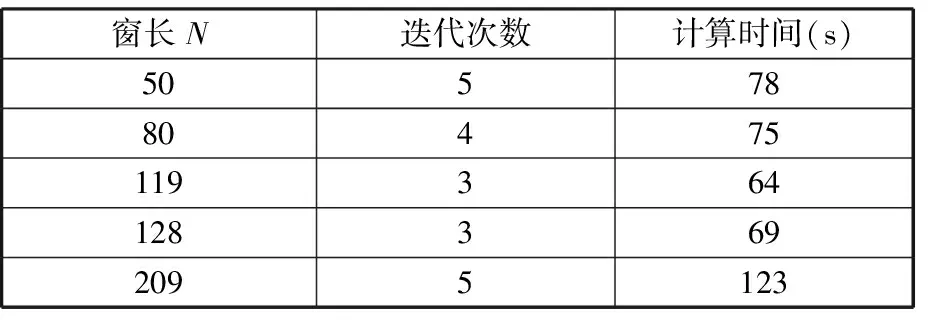
表1 不同窗長下MMD算法的迭代次數與運算時間
基于上述分析,將仿真信號s(t)的采樣頻率設置為1000 Hz,對應最優窗長為119,進行MMD分解。得到的自相關矩陣的特征值如圖3所示,可以看出,非零特征值的個數為3,即P=3,正好等于s(t)的實際分量數。根據S≥P,取S=3,經過迭代分解,結果如圖4所示。可以看出,交叉分量得到了很好的分離,得到的第三代特征向量準確地對應了仿真信號的3個分量,說明了MMD方法的有效性。
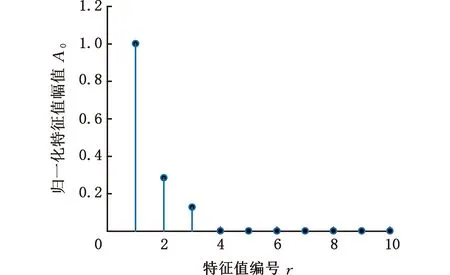
圖3 自相關矩陣的特征值Fig.3 Eigenvalues of the autocorrelation matrix
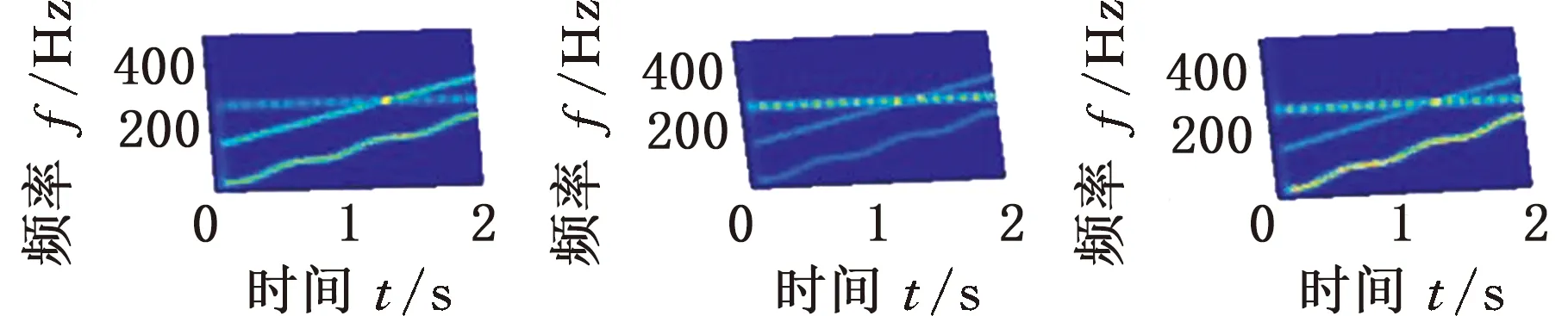
(a)初始特征向量
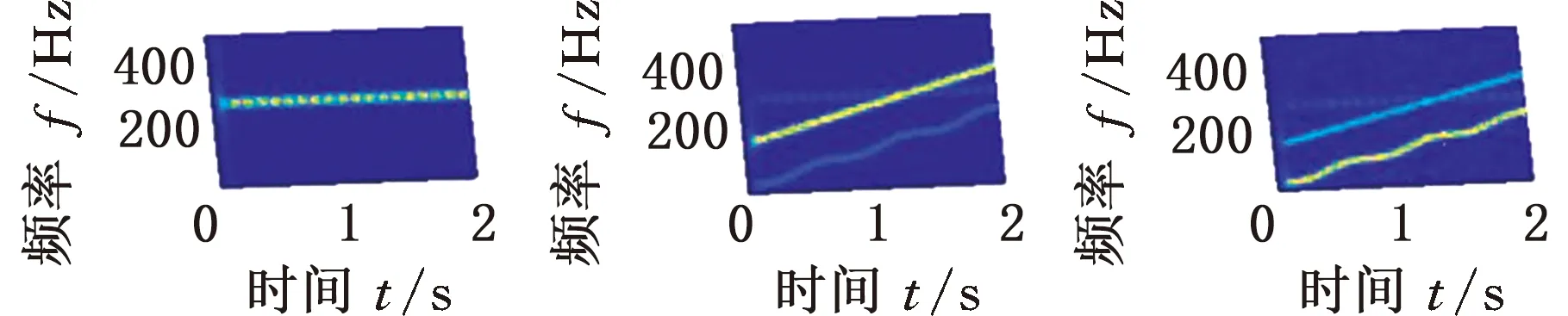
(b)第一代特征向量
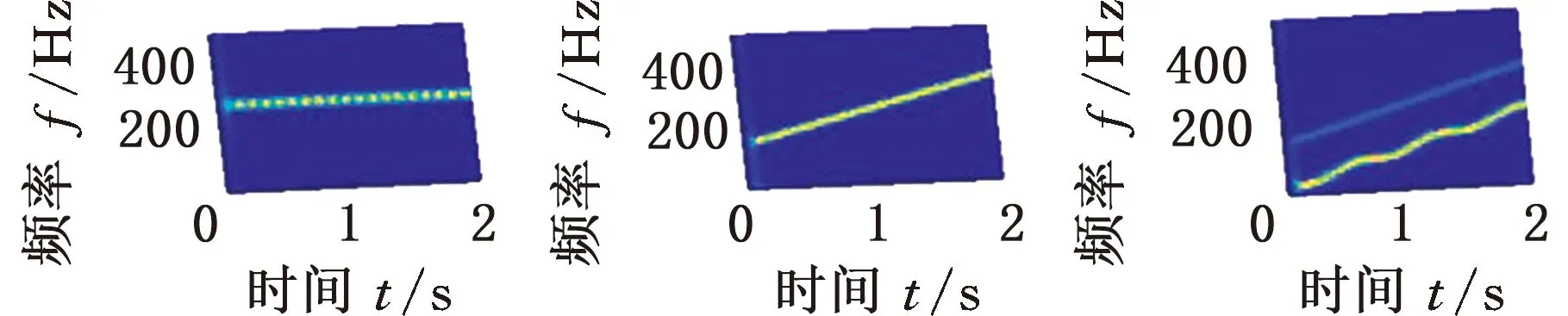
(c)第二代特征向量
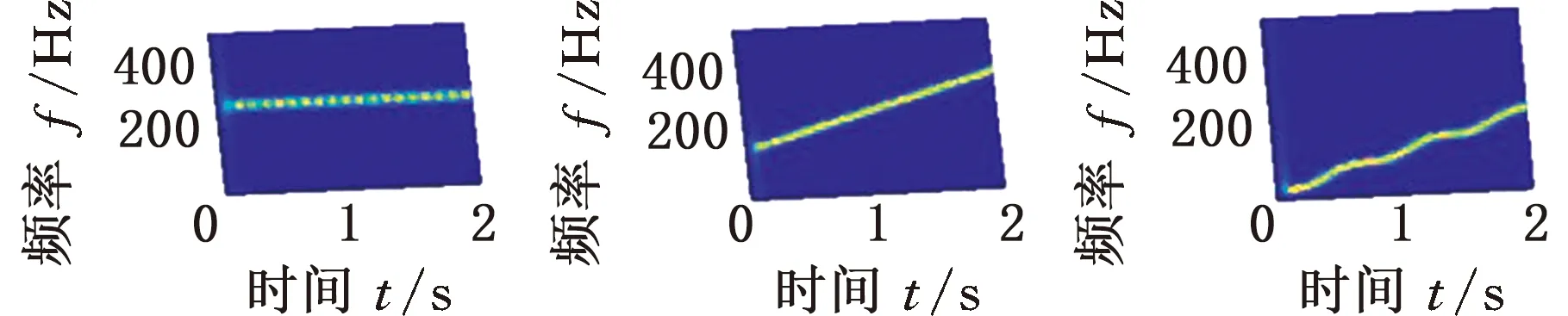
(d)第三代特征向量圖4 仿真信號s(t)的MMD分解結果Fig.4 MMD decomposition results of simulationsignal s(t)
采用目前應用廣泛的經驗模態分解(empirical mode decomposition,EMD)和變分模態分解(variational mode decomposition,VMD)方法分解仿真信號s(t),為直觀對比,分解結果也用STFT時頻圖表示。EMD與VMD分解得到的前3個分量如圖5和圖6所示。由圖5可以看出,EMD將原信號中的交叉分量當成了一個分量,而非交叉分量也由于時間尺度跨度大,被分解為兩個分量;由圖6可知,VMD算法的頻帶劃分清晰,原信號按頻率被機械地分割到3個頻帶之中,得到的3個分量均失去了物理意義。對比結果進一步說明了MMD方法的優越性。
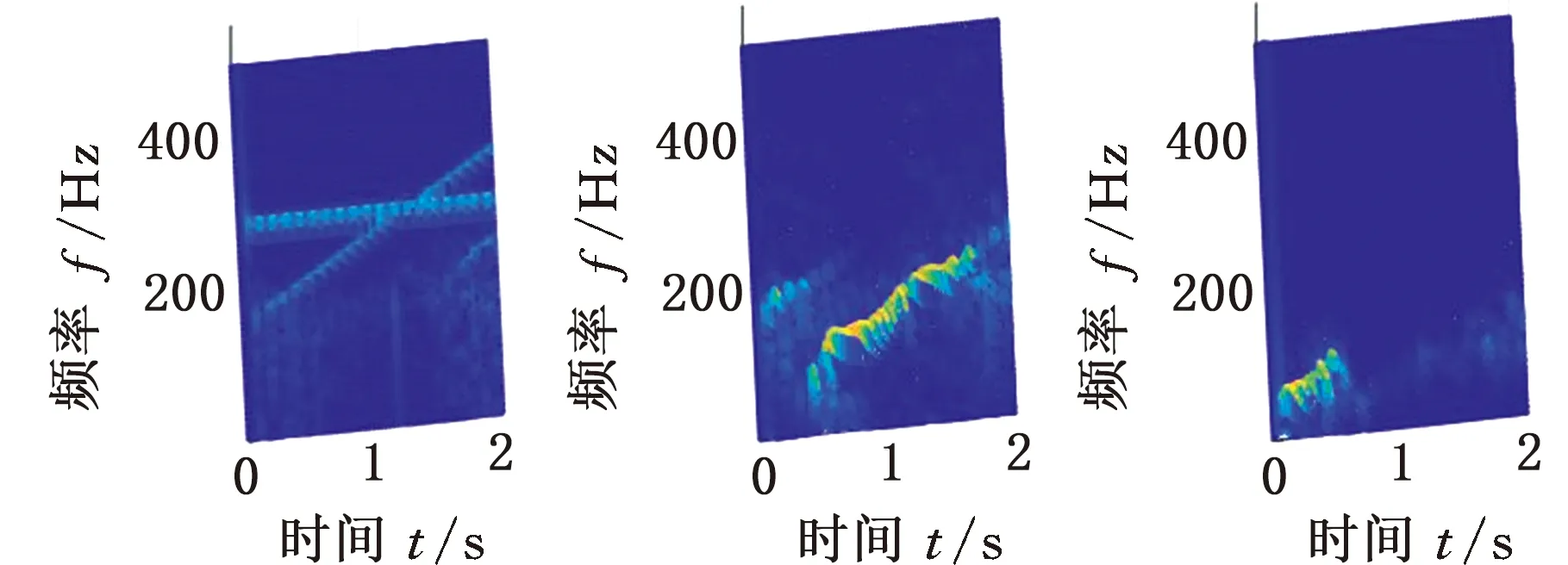
(a)IMF1 (b)IMF2 (c)IMF3圖5 仿真信號s(t)的EMD分解結果Fig.5 EMD decomposition results of simulation signal s(t)
(a)BIMF1 (b)BIMF2 (c)BIMF3圖6 仿真信號s(t)的VMD分解結果Fig.6 VMD decomposition results of simulation signal s(t)
3 在變轉速工況齒輪故障特征提取中的應用
齒輪箱包含多種運動零部件,運行時存在多種振動形式,尤其是當工作在非穩態工況時,各個部件的固有頻率振動成分與齒輪、軸承等旋轉部件的嚙合振動、故障沖擊振動等成分在時頻域很可能發生重疊。傳統的以時間尺度特征為分解依據的方法無法分離這些成分,而根據仿真信號的分析MMD方法特別適合處理該類信號。本節首先利用MMD方法對變轉速工況下的齒輪箱振動信號進行分解,將包含故障成分的分量從其他干擾分量和噪聲中分離出來,然后通過譜分析提取故障特征。
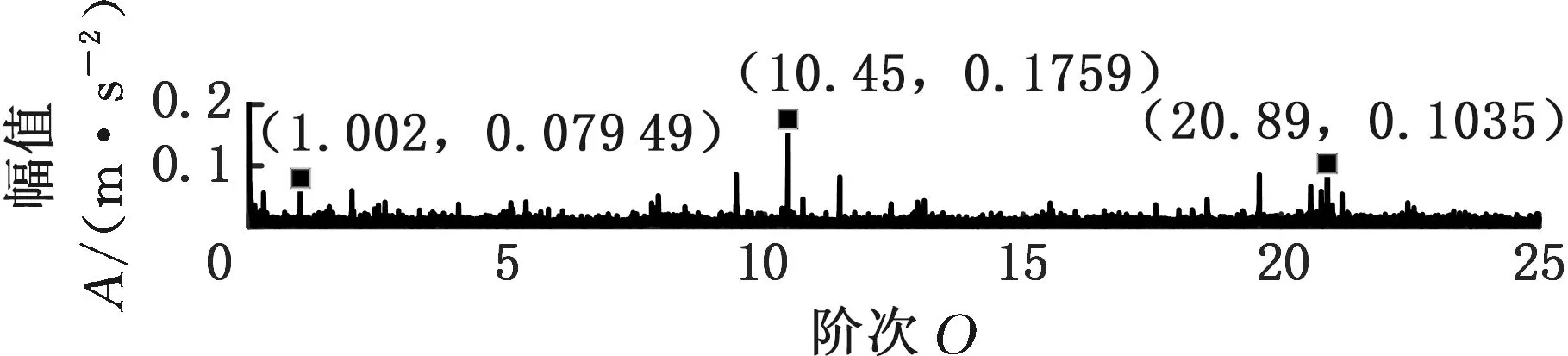
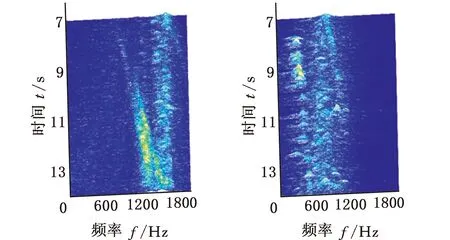
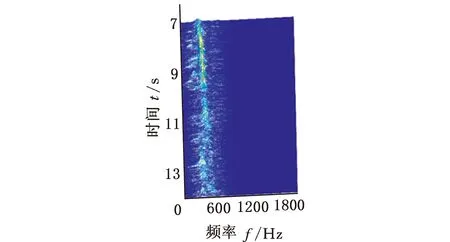
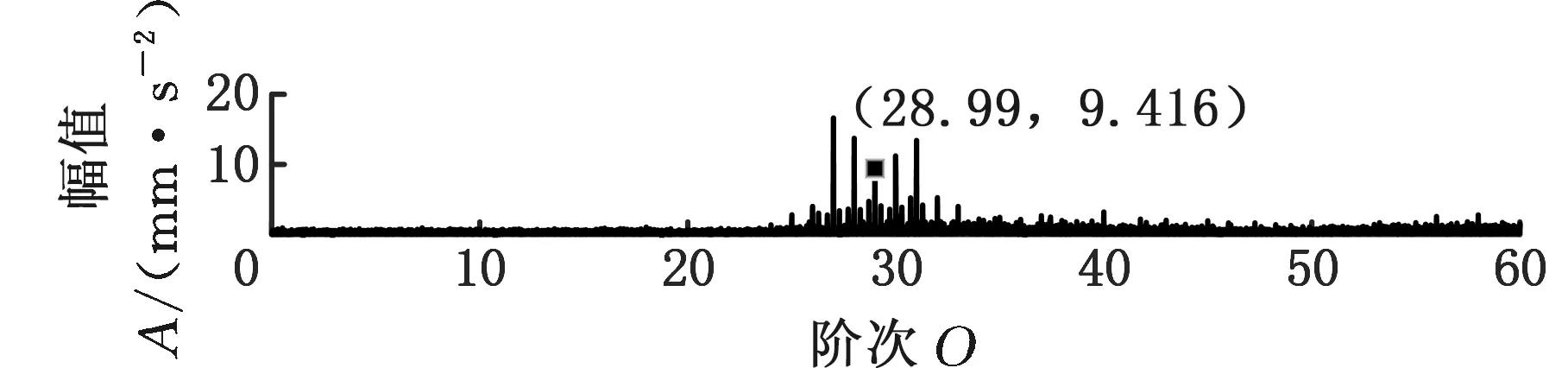
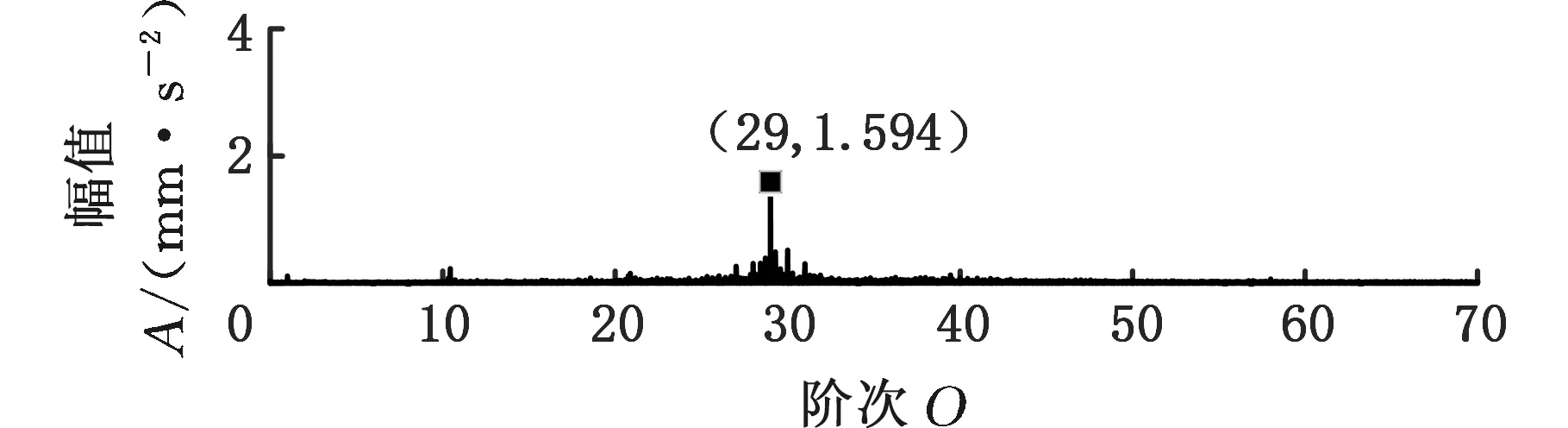
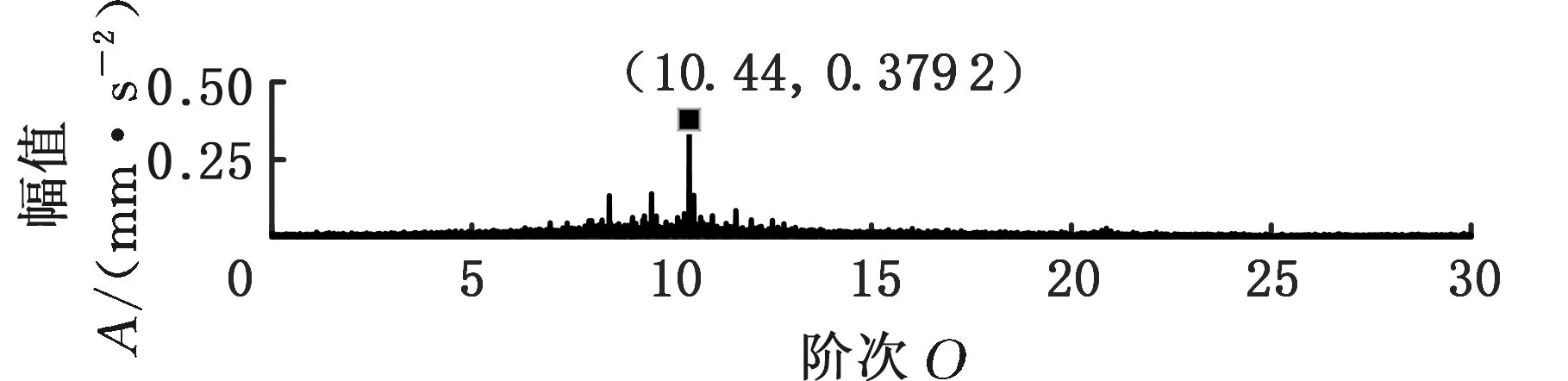
在SpectraQuest公司的旋轉機械故障模擬綜合實驗臺上進行變轉速工況下齒輪故障實驗,振動信號由5個PCB三向加速度傳感器測取,共有S=15個通道,實驗臺以及傳感器安裝位置如圖7a所示,數據采集設備為SIEMENS公司的LMS SCADAS Mobile多通道數據采集系統,如圖7b所示。故障齒輪所在齒輪箱的結構如圖8所示,轉軸Ⅰ和轉軸Ⅲ分別為輸入軸和輸出軸,齒輪1、2、3、4均為標準直齒輪,齒數分別為29、100、36和90。實驗前,分別在齒輪1和3上設置了齒面磨損和斷齒故障(實驗1)。為驗證變轉速工況下分析效果,實驗時輸入軸轉速從440 r/min增至3200 r/min,采樣頻率設置為4096 Hz,某通道的時域信號和轉軸I的轉速曲線如圖9所示,其STFT時頻圖見圖10a。可以看出,分布有包括隨轉速變化的齒輪嚙合振動、故障沖擊振動以及不隨轉速變化的部件固有頻率振動等多種振動成分,且這些成分跨時間尺度特征大,成分之間存在多處交叉,分布復雜。

(a)旋轉機械故障模擬綜合實驗臺

(b)LMS SCADAS Mobile多通道數據采集系統圖7 旋轉機械故障實驗臺與數據采集系統Fig.7 Rotating machinery fault test bench and dataacquisition system
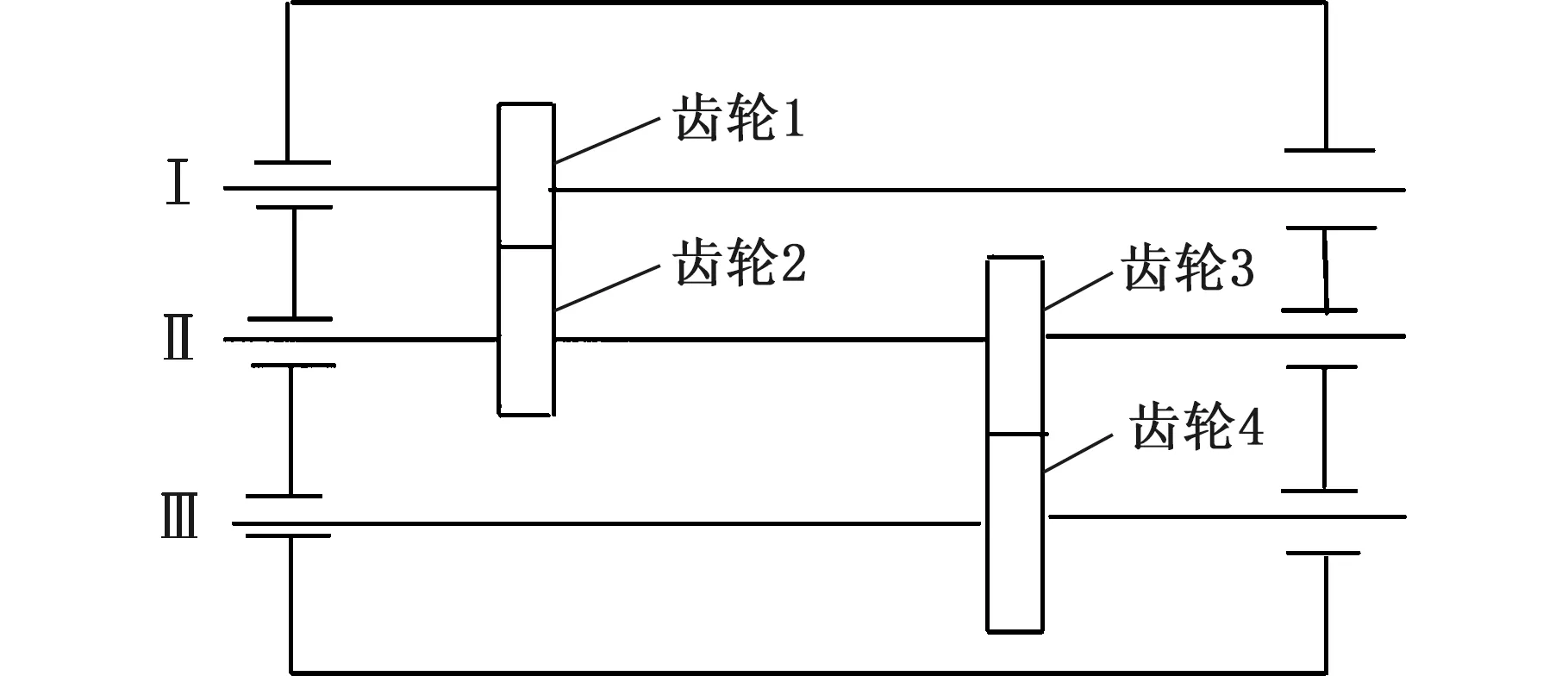
圖8 齒輪箱結構簡圖Fig.8 Structural diagram of gearbox
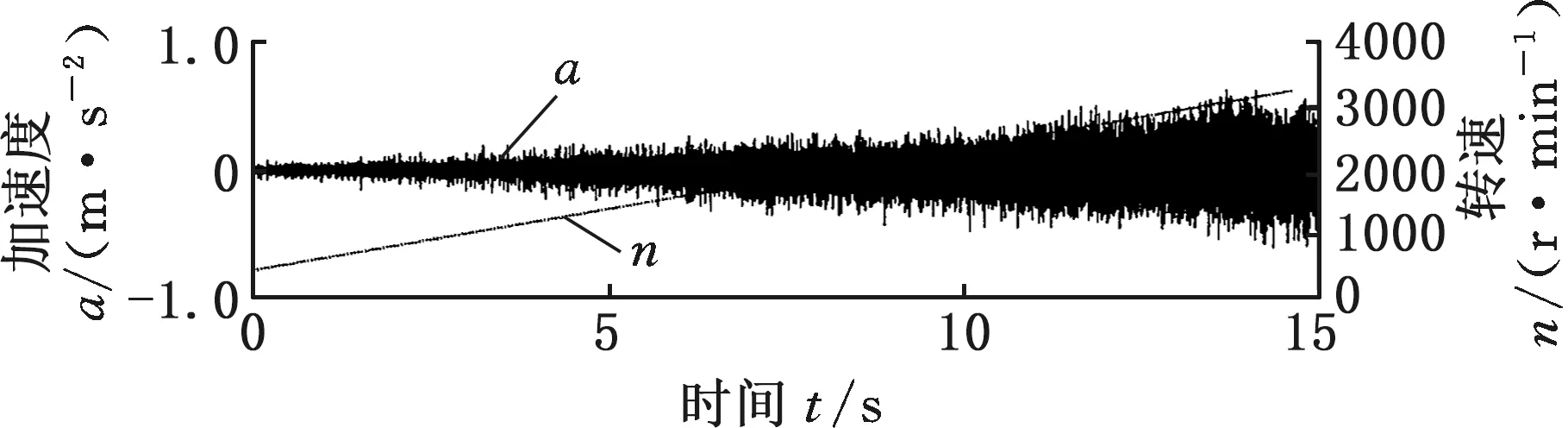
圖9 某通道時域信號與轉軸Ⅰ轉速曲線Fig.9 Time domain signal of a channel and rotatingspeed curve of shaft Ⅰ
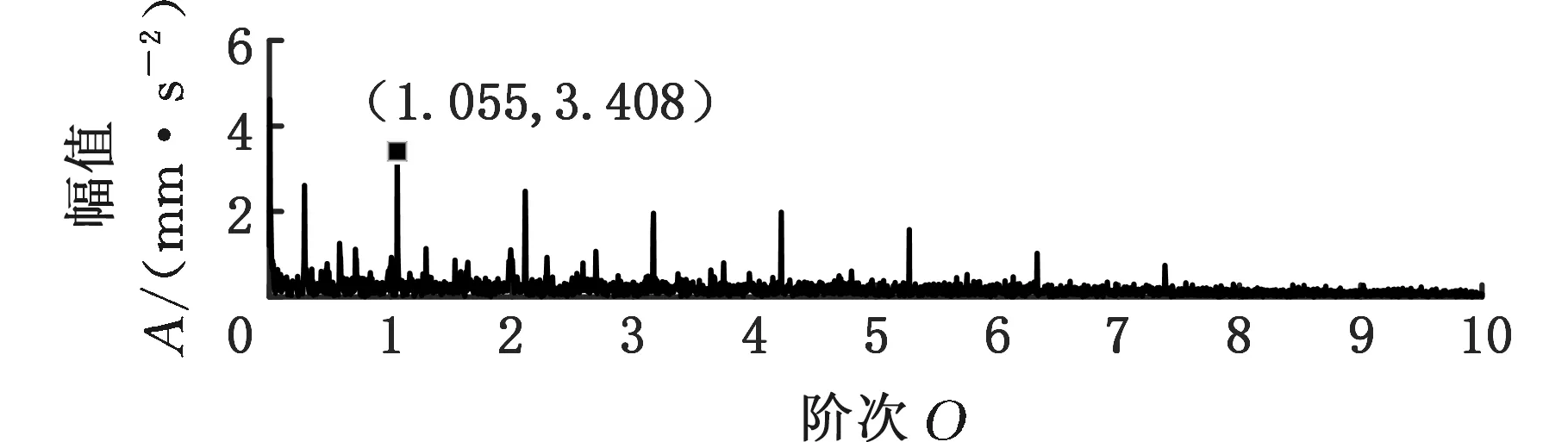
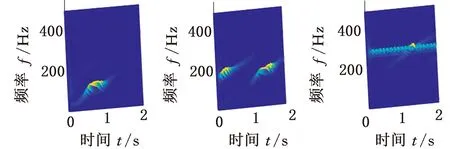
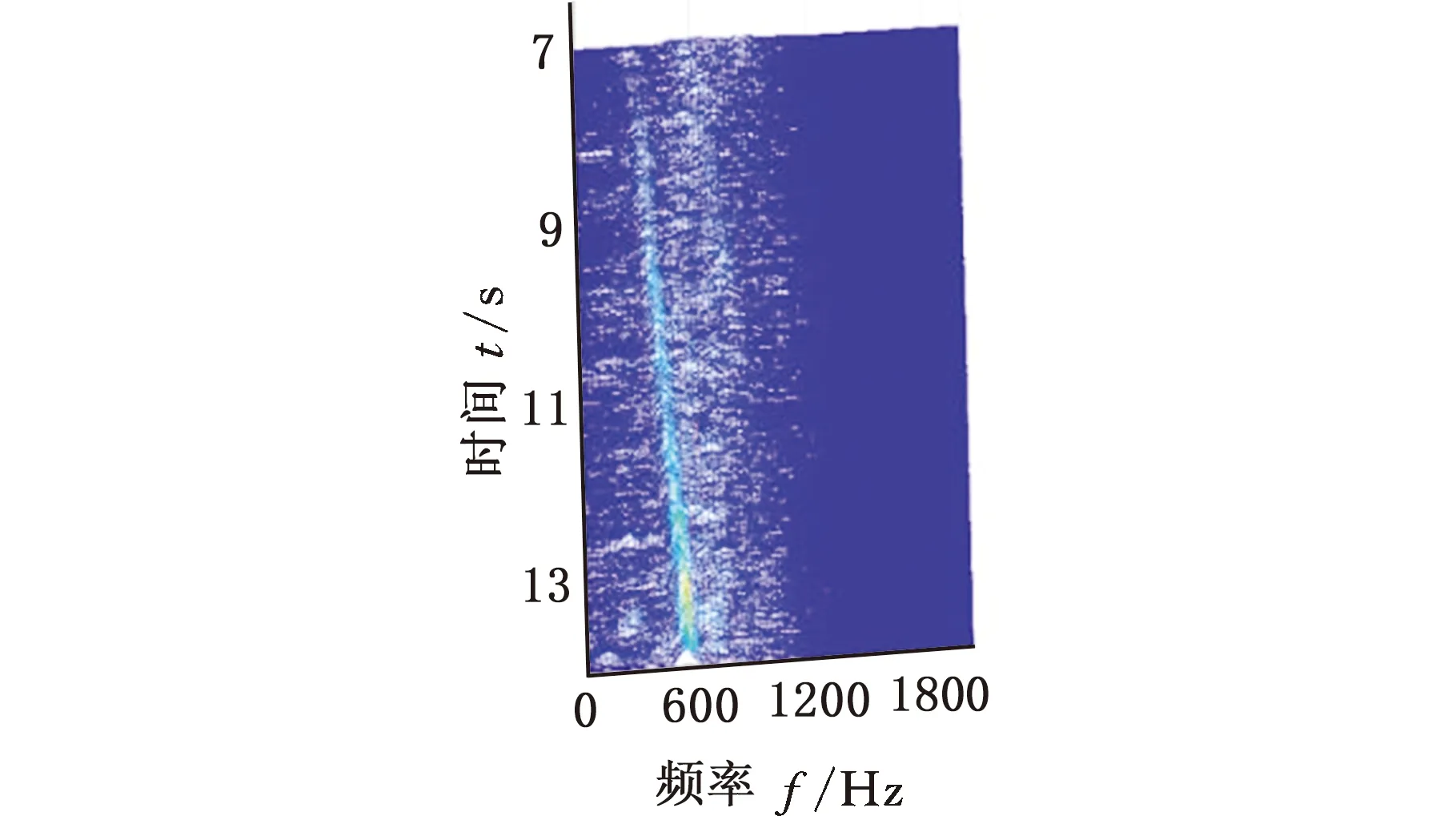
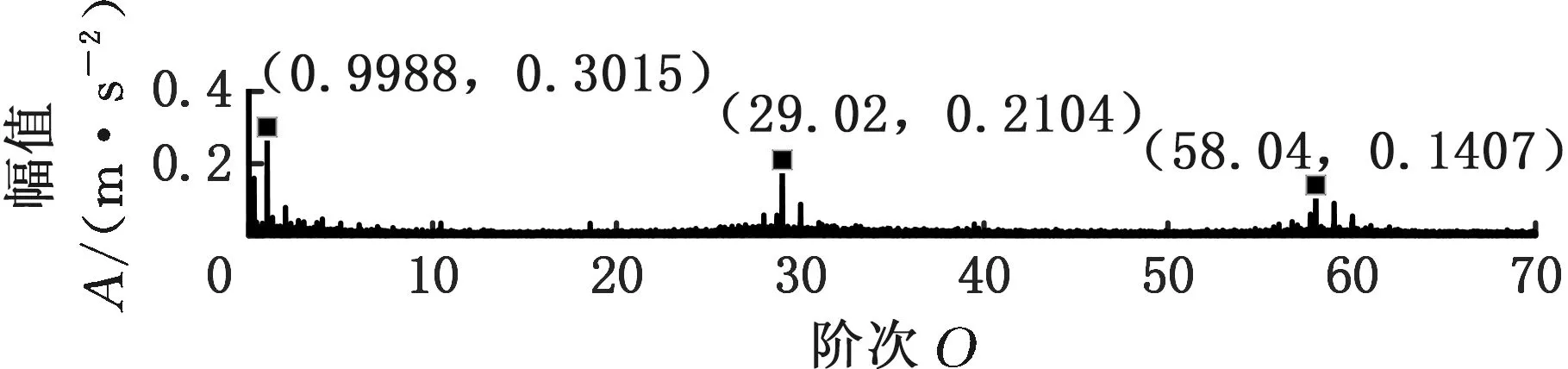
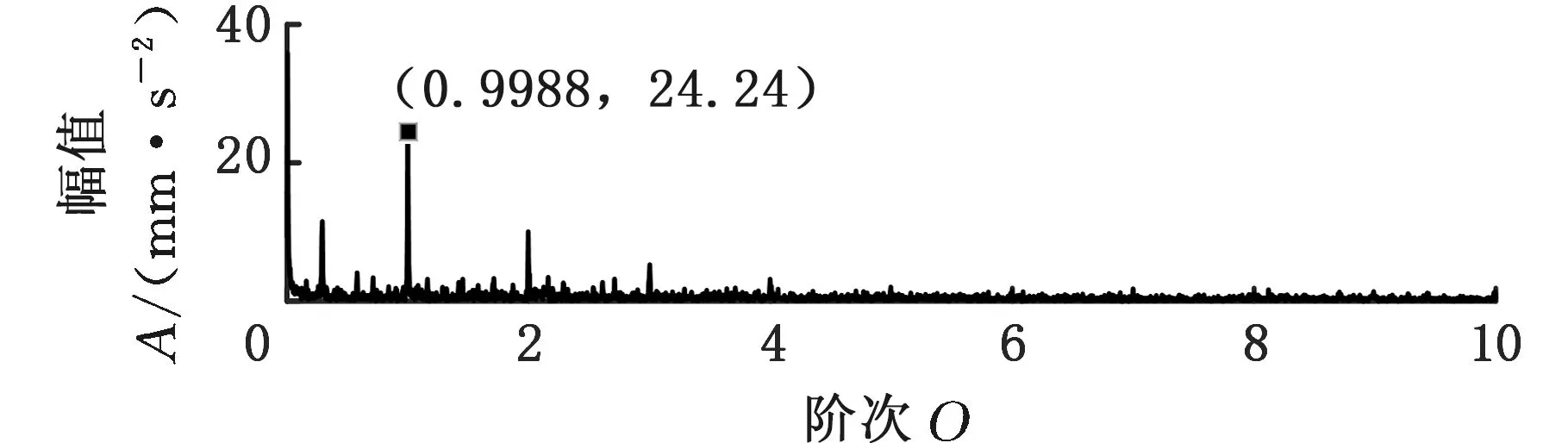
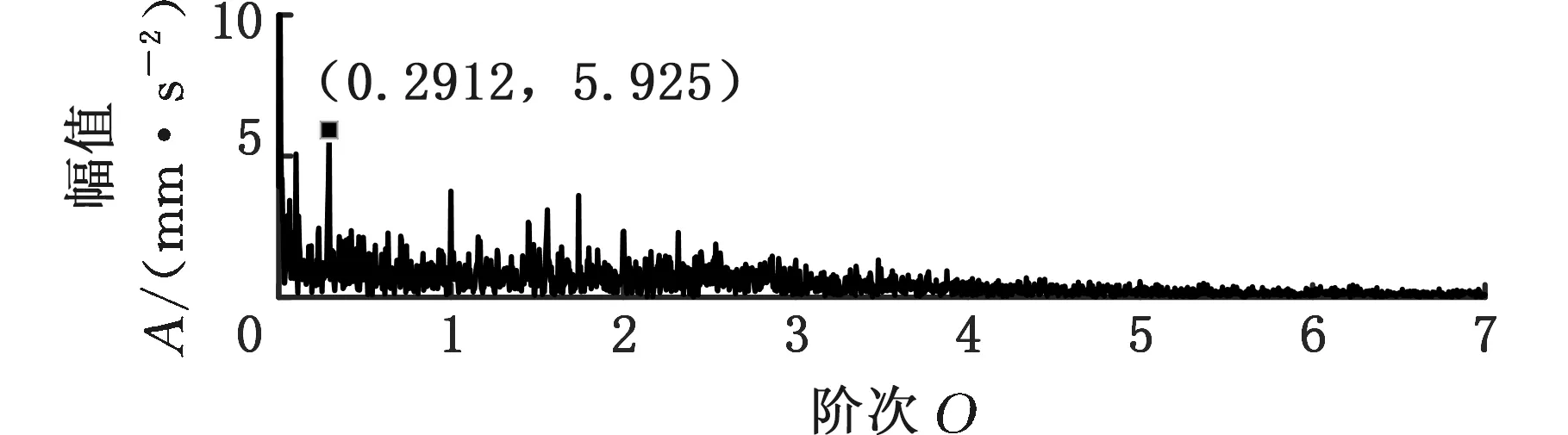
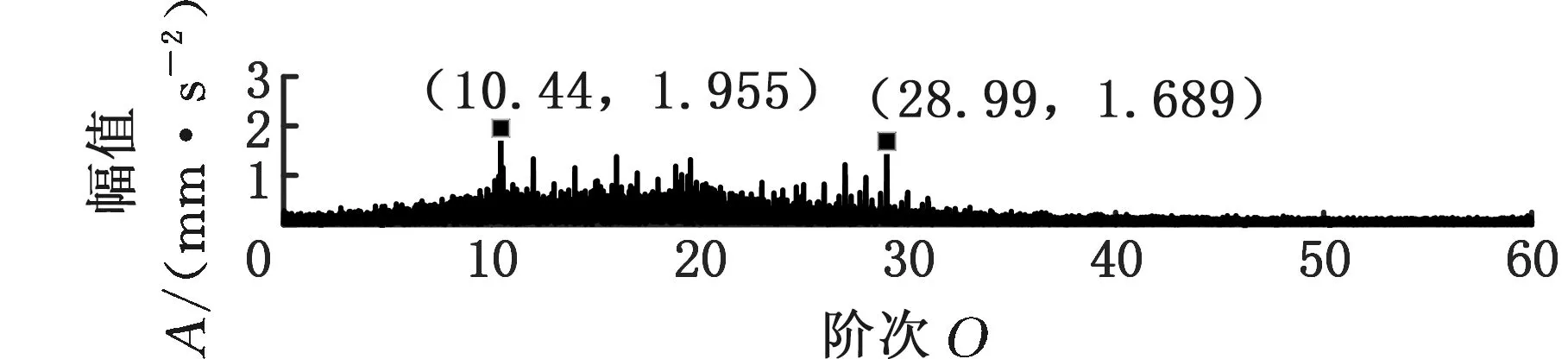
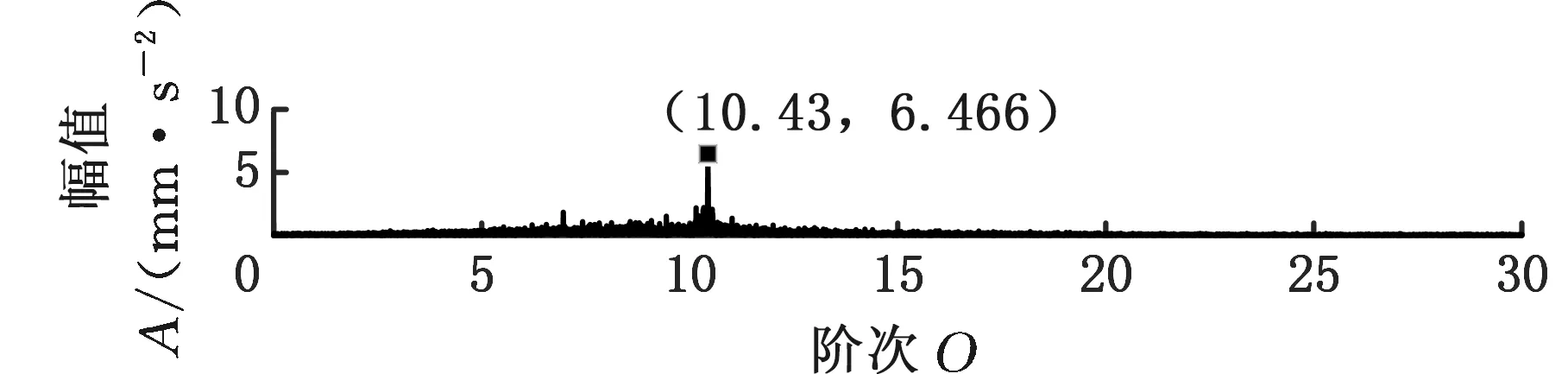
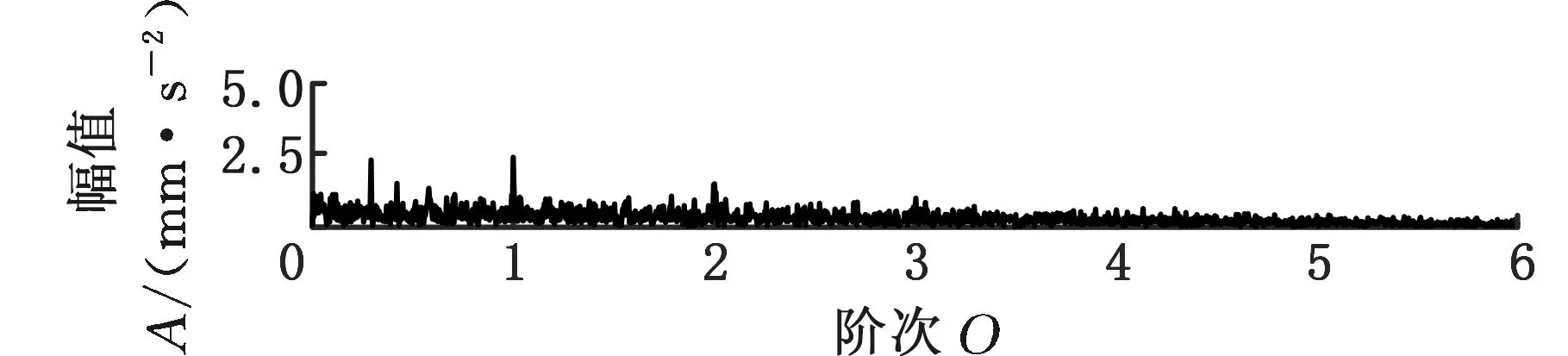
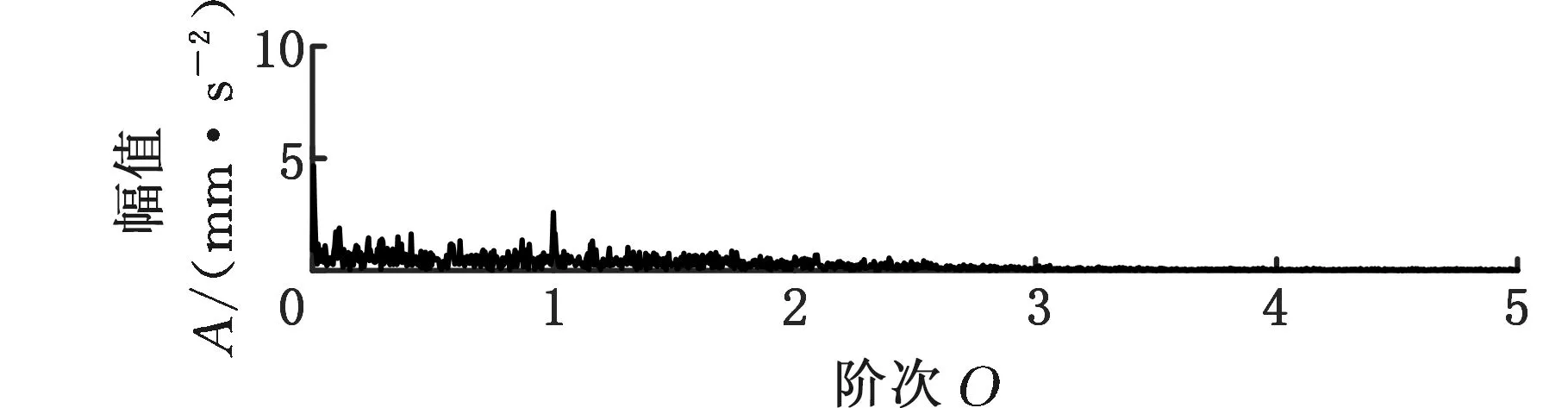
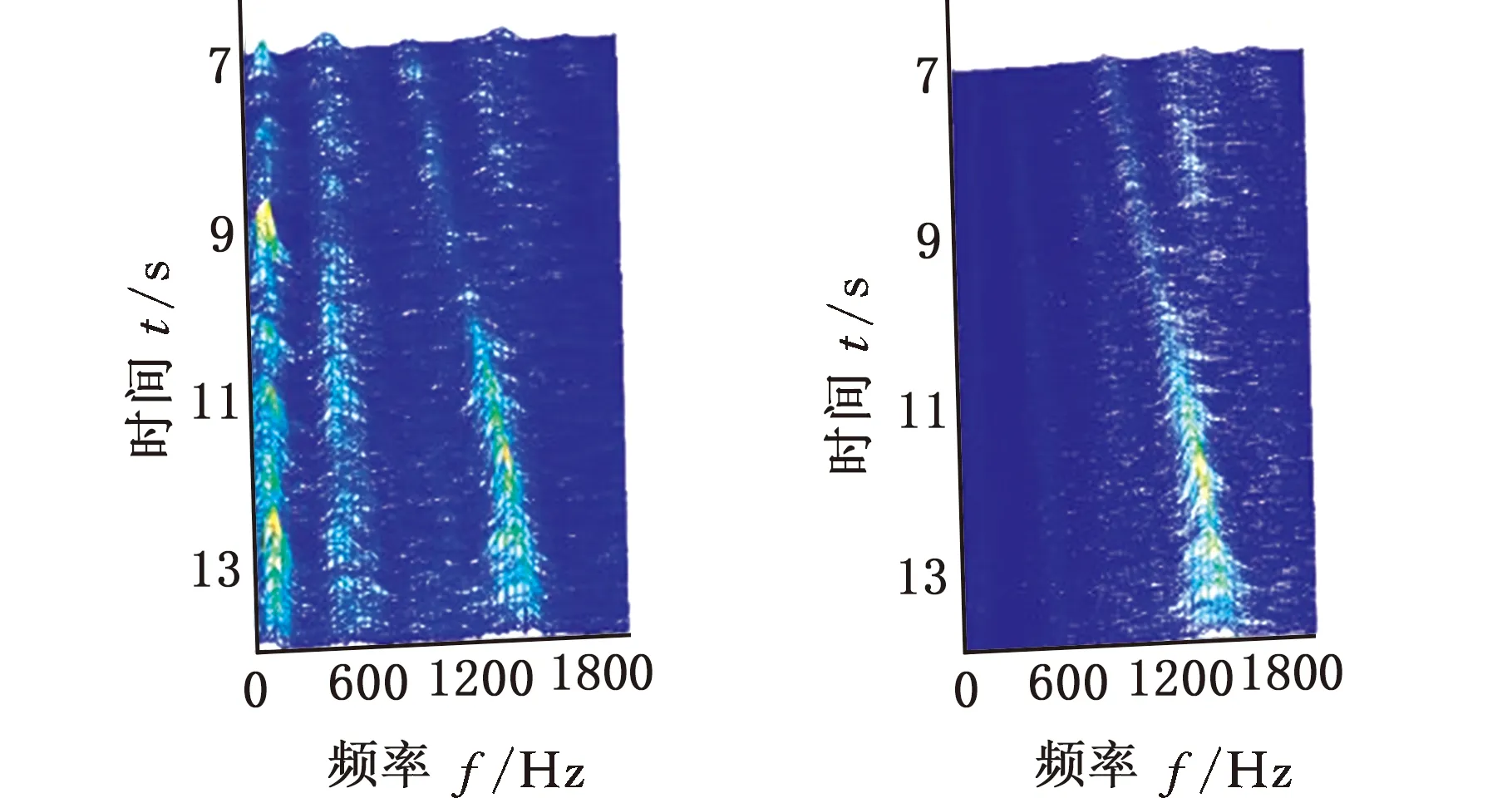
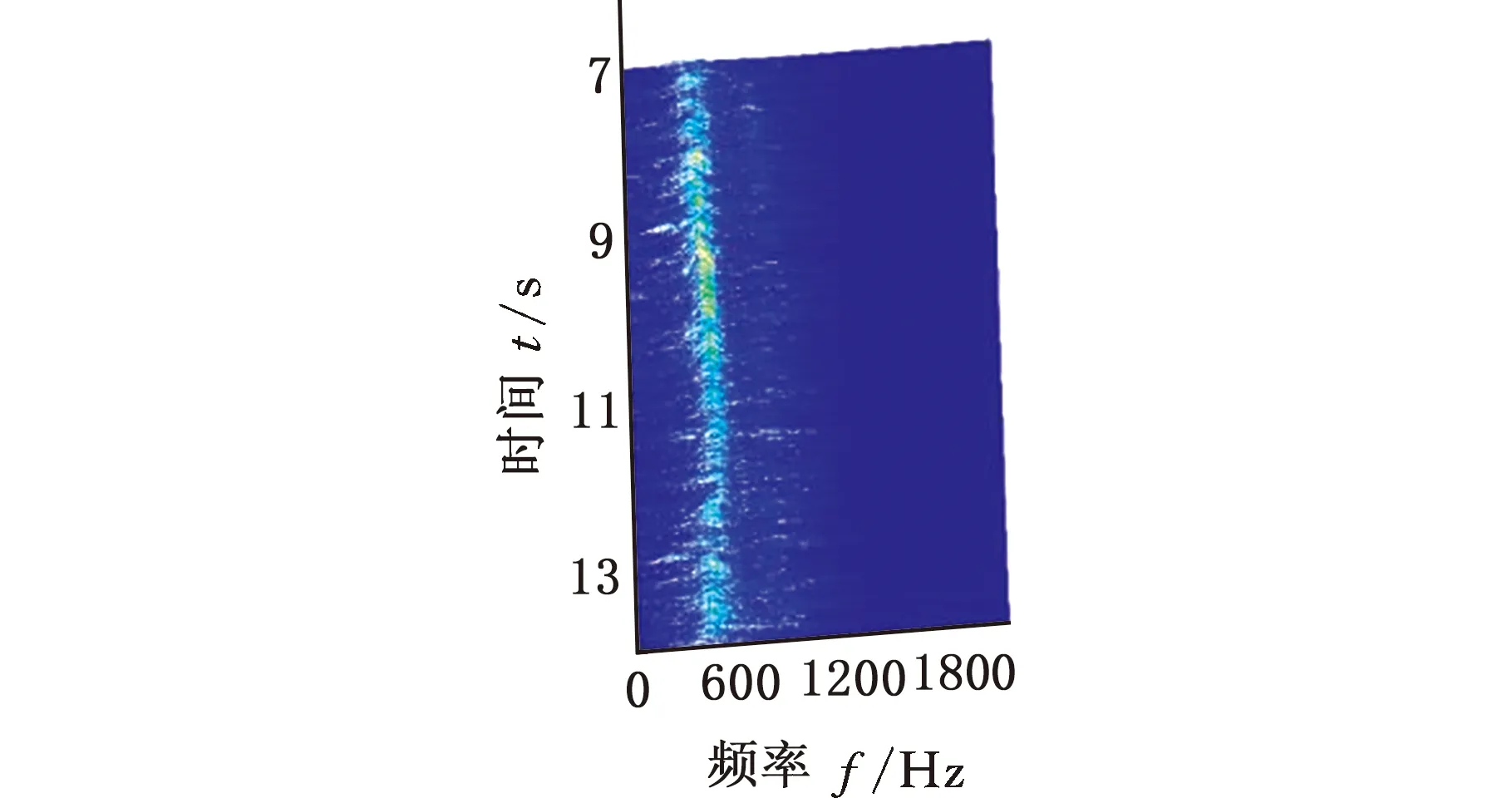
采用MMD方法進行處理,根據時頻圖的分布情況,預設分量數P=5 (a)某通道信號STFT時頻圖 (b)分量1 STFT時頻圖 (c)分量2 STFT時頻圖圖10 變轉速工況齒輪箱振動信號(實驗1)的MMD分解結果Fig.10 MMD decomposition results of variable rotatingspeed condition gearbox vibration signal(experiment 1) (a)分量1階次譜 (b)分量2階次譜圖11 分量1和分量2的階次譜Fig.11 Order spectrum of the first component andthe second component (a)分量1包絡階次譜 (b)分量2包絡階次譜圖12 分量1和分量2的Hilbert包絡階次譜Fig.12 The Hilbert envelope order spectrum of the firstcomponent and the second component 對分量1和2進行階次譜分析,結果如圖11所示,兩對齒輪副的理論嚙合階次分別為O1=29和O2=10.44。由圖11a可以看出,在階次29.02、58.04處有清晰的譜線,對應齒輪1和2的一倍和二倍嚙合階次,并且在其兩邊有不對稱的調制邊頻帶;由圖11b可以看出,在階次10.45、20.89處有清晰的譜線,對應齒輪3和4的一倍和二倍嚙合階次,同樣在其兩旁有不對稱的調制邊頻帶。為判斷邊頻特征,對分量1和2的Hilbert包絡信號進行階次分析,結果如圖12所示。可以看出,圖12a中在階次0.9988處有明顯峰值;圖12b中在階次0.2912處有明顯峰值,分別對應了轉軸Ⅰ和轉軸Ⅱ的轉頻階次,這說明齒輪嚙合振動成分被轉頻調制,符合齒輪出現局部故障時的故障機理,驗證了MMD方法結合階次分析可有效提取變轉速工況下的齒輪故障特征。 (a)IMF1 STFT時頻圖 (b)IMF2 STFT時頻圖 (c)IMF3 STFT時頻圖圖13 變轉速工況齒輪箱振動信號的EMD分解結果Fig.13 EMD decomposition results of variable rotatingspeed condition gearbox vibration signal 為了對比,采用EMD方法對圖9所示信號進行分解,得到的前3個IMF分量如圖13所示,為了直觀比較,同樣采用STFT時頻表示。可以看出,由于轉速變化,時間尺度跨度大,導致兩個嚙合振動分量的不同部分被分解到了3個分量之中,失去了原有的物理意義,并且嚙合振動分量與重疊的固有振動成分也未完全分離,同時還存在較為嚴重的背景噪聲。對3個IMF分量及其包絡信號進行階次譜分析,結果如圖14和圖15所示。在圖14中雖然存在嚙合階次,但由于受到其他成分和噪聲的干擾,表現不明顯;而在圖15中與轉頻調制相關的特征階次也不明顯,尤其是轉軸Ⅱ的轉頻階次。通過對比說明了MMD方法的優勢。 (a)IMF1階次譜 (b)IMF2階次譜 (c)IMF3階次譜圖14 前3個IMF分量的階次譜Fig.14 Order spectrum of the first threeIMF components (a)IMF1包絡次譜 (b)IMF2包絡次譜 (c)IMF3包絡次譜圖15 前3個IMF分量的Hilbert包絡階次譜Fig.15 The Hilbert envelope order spectrum of thefirst three IMF components 將斷齒齒輪3換成同型號正常齒輪進行實驗(實驗2),實驗工況與分析方式同前。原始信號及分解得到的分量1和2如圖16所示,可以看出,MMD清晰地分解出了兩個嚙合振動分量,分解效果良好。分量1和2及其包絡信號的階次譜如圖17和圖18所示,可以看出,在階次譜中齒輪1和2的嚙合階次兩旁有明顯的邊頻帶,而齒輪3和4的嚙合階次旁邊頻帶不明顯;在包絡階次譜中主要存在轉軸Ⅰ的轉頻及其倍頻階次,而轉軸Ⅱ的轉頻階次不明顯,這符合齒輪箱實際狀況,進一步說明了MMD方法的有效性。 (a)IMF1 STFT時頻圖 (b)IMF2 STFT時頻圖 (c)IMF3 STFT時頻圖圖16 變轉速工況齒輪箱振動信號(實驗2)的MMD分解結果Fig.16 MMD decomposition results of variable rotatingspeed condition gearbox vibration signal(experiment 2) (a)分量1階次譜 (b)分量2階次譜圖17 分量1和分量2的階次譜Fig.17 Order spectrum of the first component and thesecond component (a)分量1包絡階次譜 (b)分量2包絡階次譜圖18 分量1和分量2的Hilbert包絡階次譜Fig.18 The Hilbert envelope order spectrum of thefirstcomponentand the second component 本文將一種全新的多通道多分量分解(MMD)方法引入變轉速工況齒輪故障特征提取,在采用對數窗能量準則提高時頻聚集性度量準確性與效率的基礎上,將MMD方法應用于具有復雜時頻特征的齒輪箱振動信號分析,得到了以下結論: (1)對數窗能量準則能自適應地確定不同采樣率下的最佳窗長,融入了對數窗能量準則的MMD方法可減少算法迭代次數和計算時間,為實際振動信號分析提供參考。 (2)通過仿真信號的分析表明,相比于經典的EMD和VMD方法,MMD方法對時間尺度跨度大且時間尺度有重疊的復雜信號具有明顯分解優勢。 (3)通過對變轉速工況齒輪箱振動信號的分析表明,MMD方法可從時頻分布復雜的振動信號中有效分解出含有故障特征的分量成分,為齒輪故障特征提取提供了新的有效途徑。 另外值得說明的是,MMD方法是基于多通道數據的,但在某些實際工程設備的齒輪箱上安裝多個振動傳感器可能會受到限制。對于此種情況:一是因為信號之間只要存在相位差,MMD方法就會認為其是不同通道的信號,而實際情況下不同傳感器或同一傳感器不同方向測得的信號都存在相位差,因此在安裝受限的條件下,可以考慮將不同傳感器盡可能地緊鄰布置在可安裝的部位;二是雖然實際振動信號可能包含的分量較多,但包含故障特征的分量一般為前幾階分量,即只要分解出前幾個主要分量即可,因此大部分情況下所需的傳感器數量不多;三是對于極端情況,如果條件允許,可以嘗試在齒輪箱上增加一個放置傳感器的裝置;反之,可以嘗試對采集的單通道振動數據人為設置相位差,從而變為多通道的數據,這是基于雖然相位不同,但其中的分量成分的頻率特征不會發生改變,即不會對故障特征提取造成影響,這也是后續的研究方向之一。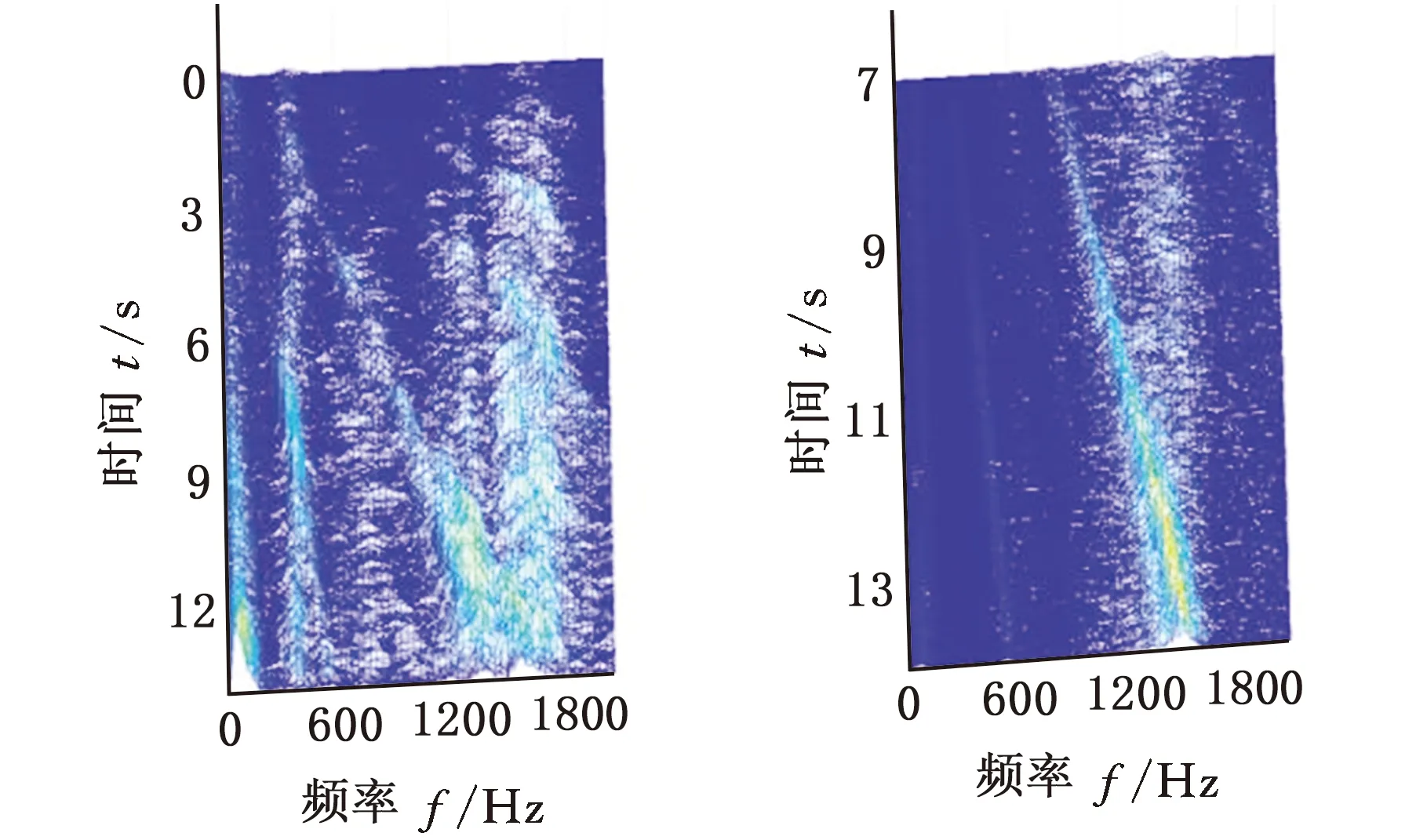

4 結論