匹配和不匹配干擾共存時電液伺服系統預設性能漸近跟蹤控制

董振樂 楊英浩 姚建勇 張 政 李閣強 王 帥

1.河南科技大學車輛與交通工程學院，洛陽，4710002.浙江大學流體動力與機電系統國家重點實驗室，杭州，3100273.南京理工大學機械工程學院，南京，2100944.河南省機械裝備先進制造協同創新中心，洛陽，471000

0 引言

電液伺服系統相比機電和氣壓系統具有功率質量比高、負載能力強等突出優勢，在工業和國防領域有廣泛應用[1-3]。隨著裝備性能不斷升級，對電液伺服系統在服役過程中的運動/力精度要求愈發苛刻。對此，除需高性能的液壓元件和系統集成設計作為支撐外，控制策略的需求也十分迫切，由于液壓件研發周期長，優良的控制策略成為系統性能提升的關鍵途徑。電液伺服系統存在諸多非線性環節和時變干擾，非線性環節有控制輸入-負載流量非線性和負載壓力-負載流量非線性等[4]，時變干擾則分為不匹配干擾(即不在控制通道內，如負載運動時所受環境外干擾、強密封下的難以精確建模的摩擦干擾等)和匹配干擾(即在控制通道內，如難以預測的外泄漏，不同工況下參數變化與狀態耦合引起的干擾等)，這些均給控制策略的設計帶來很大難度。

針對電液伺服系統非線性，相關學者通過對各類非線性環節進行更精細的建模或模型辨識，實現了較好的補償效果，如余臻等[5]、YAO等[6]、HELIAN等[7]。而如何處理時變干擾成為現階段電液伺服系統非線性控制策略研究的主要關注點。YAO等[8]提出融合反步設計和不連續映射的自適應魯棒控制策略，同時處理了匹配干擾和不匹配干擾；GUAN等[9]針對含有非線性不確定參數的電液控制系統, 提出了一種滑模自適應控制方法，削弱了由于初始控制容積不確定引起的非線性不確定參數匹配干擾對控制性能的影響；YAO等[10-11]提出基于誤差符號積分(RISE)的控制方法，先后實現了電液伺服系統在不匹配干擾或匹配干擾下的高精度控制，后續又提出自抗擾自適應控制方法[12]，實現了系統在匹配和不匹配常值干擾共存時的穩態漸近控制；張震陽等[13]提出采用擴張狀態觀測器(ESO)的估計匹配干擾，提高了系統跟蹤精度。

上述研究均針對穩態性能進行控制設計，其最理想的理論結果是漸近穩定，即控制誤差隨時間理論上逐漸趨近于零，然而，當匹配和不匹配時變干擾共存時，尚未有文獻獲得漸近控制結果。此外，當系統運行初始位置和指令初始位置不一致時，或在某些短時動作場合(如模鍛電液錘、液壓彈射等)，瞬態性能(如超調量、收斂速度等)對系統運行質量十分重要，因此，將瞬態性能和穩態性能并重，才可確保系統高質量地輸出運動或力，而現有研究鮮有將兩者兼顧。董振樂等[14]基于預設性能函數[15]改善了系統瞬態控制性能，然而對于存在干擾時的穩態控制精度，并未獲得最佳的理論結果，原因是電液伺服系統模型結構使得傳統漸近穩定設計方法(如RISE和滑模等)很難融入預設性能函數，且無法同時處理匹配和不匹配干擾，甚至面臨高增益反饋的風險，如何克服這個難題成為本研究的出發點。

綜合以上考慮，本文針對電液伺服系統匹配和不匹配干擾共存的特點，兼顧瞬態性能和穩態性能需求，提出一種新型高精度控制策略。以電液位置伺服系統為例，建立了包含匹配和不匹配干擾的非線性數學模型，定義預設性能函數規劃控制誤差，并融合反步設計和采用干擾上界估計的連續漸近控制技術處理匹配和不匹配干擾，最終獲得可預設的瞬態性能和漸近穩態性能，實現高精度跟蹤控制。

1 系統建模

本文所考慮的電液位置伺服系統原理如圖1所示，由伺服閥控制液壓缸兩腔流量進而控制兩腔壓力，實現對活塞桿伸出長度的控制，活塞桿外接負載，最終可實現負載執行件的位置調節。

圖1 電液伺服系統原理示意圖Fig.1 The sketch of electro-hydraulic position servo system

根據牛頓第二定律，負載動力學方程為

(1)

pL=p1-p2

壓力動態方程可由下式描述[4]：

(2)

高性能伺服閥的頻寬高達上百赫茲，其響應遠高于整個伺服系統的響應，建模時可忽略伺服閥的動態，視輸入電壓u和伺服閥芯位移xv之間為比例環節，即xv=kuu。根據文獻[4]可知負載流量qVL和伺服閥輸入電壓u的關系：

(3)

式中,kq為流量增益；Cd為伺服閥節流孔系數；w為伺服閥節流孔面積梯度；ρ為液壓油密度；ps為系統供油壓力，系統回油壓力為零。

(4)

g2=4Aβe/Vtg3=4Ctβe/Vt

2 控制器設計

2.1 預設性能函數

定義位置跟蹤誤差e1=x1-x1d，假設因負載任務設定，跟蹤誤差需滿足以下性能指標：

-δρ(t)0

(5)

(6)

顯然，式(5)和式(6)對跟蹤誤差e1作出了如下預設：-δρ0和δρ0分別預設了跟蹤誤差的最大下沖量和最大超調量，參數k預設了跟蹤誤差的收斂速度，ρ∞預設了跟蹤誤差的穩態收斂域。

進一步定義如下遞增函數：

(7)

分析式(7)可知，根據遞增函數S(z1)的性質，式(5)顯然等價于e1(t)=ρ(t)S(z1)，且當z1有界時，式(7)始終成立。下面給出一個可用的函數S(z1)[15]:

(8)

為了便于后續推導，將S(z1)記為λ。

求式(8)反函數：

(9)

接下來基于轉換誤差z1設計最終控制器。

2.2 控制器設計

對式(9)求導，可得

(10)

進一步可得

(11)

(12)

設計穩定函數α2為

(13)

式中，k2為正的可調反饋增益；α2a用于前饋補償相應的系統動態函數和預設性能函數；α2s1為線性魯棒穩定項。

將式(13)代入式(12)，可得

(14)

設計式(13)中的α2s2如下[16]:

(15)

式(15)中α2s2顯然是連續的，通過其實現對不匹配干擾的漸近抑制，證明過程隨后給出。

同樣，結合前文定義及式(4)，有

(16)

(17)

根據式(16)，最終控制器可設計為

(18)

式中,k3為正的可調反饋增益；ua用于前饋補償相應的系統動態；us1為線性魯棒穩定項。

將式(18)代入式(16)，可得

(19)

則可設計us2如下[16]：

(20)

式(20)中us2顯然是連續的，通過它實現對匹配干擾的漸近抑制，證明過程隨后給出。

對于函數ε1(t)和ε2(t)，令其滿足

(21)

2.3 控制器性能

(1) 整個電液位置伺服閉環系統中所有信號都是有界的，即系統不會失穩，且位置控制誤差具有式(5)、式(6)所預設的瞬態性能。

(2) 系統最終漸近穩定，即當時間t趨近于無窮時，位置誤差e1趨近于零。

證明：詳情掃描OSID二維碼獲得。

所提出的控制器總體框圖見圖2。

圖2 控制器總體框圖Fig.2 The overall block diagram of the controller

3 試驗驗證

圖3所示為電液位置伺服系統試驗平臺，由機械底座、伺服閥(Moog G761-3003，流量19 L/min，頻寬不小于120 Hz)、光柵尺(Heidenhain LC483，精度±5 μm)、壓力傳感器(MEAS US175-C00002-200BG，精度0.1 MPa)、液壓缸組件(行程44 mm，有效作用面積904.78 mm2)和負載質量塊(30 kg)組成，控制系統A/D卡采用研華PCI-1716，D/A卡采用研華PCI-1723，計數卡采用Heidenhain IK-220，基于LabWindows-CVI平臺建立人機交互、運動監控和指令模塊，采樣時間0.5 ms。

圖3 試驗平臺Fig.3 Experimental platform

為了充分驗證所設計控制器的有效性，選取以下4種控制器進行對比試驗：

(1)PID，即經典的比例-積分-微分控制，調試后的參數為kP=420，kI=120，kD=0。

(2)FLC，即反饋線性化控制，用于驗證所建立數學模型對控制性能的補償效果。基于系統模型(式(4))，該控制器的結構為

(22)

式中，μ1為位置控制誤差；μ2、μ3為輔助設計誤差；k1、k2、k3為正的反饋增益；ψ為穩定函數。

調試后，控制器各參數選取為：k1=300，k2=100，k3=0.0002。

(4)PPC，即僅具有預設瞬態性能的控制器，可參考文獻[14]，相比本文設計控制器，該控制器中不包含漸近穩定設計，即去掉式(15)的α2s2以及式(20)中u2s2。為了確保對比的有效性，控制器參數取值同PPAC。

3.1 試驗工況一

圖4 工況一位置指令Fig.4 Command position for condition one

圖5為4種控制器作用下的跟蹤誤差對比曲線，另外計算了前兩個運動周期和最后兩個運動周期的最大跟蹤誤差emax，如表1所示。顯然，FLC控制器由于包含模型補償成分，相比PID控制器，穩定階段的最大跟蹤誤差由0.641mm減小至0.265 mm，而由于FLC控制器包含了系統參數信息，參數偏差導致其初始階段最大跟蹤誤差相比于PID由0.035 mm增至0.058 mm。當控制器中加入預設性能函數后，在函數的規劃作用下，PPC控制器初始階段和穩態階段的最大跟蹤誤差分別為0.027 mm和0.112 mm，相比于PID和FLC控制器，初始階段跟蹤精度提高均超22.9%，穩態階段跟蹤精度提高均超過57.73%。在控制器中加入基于干擾上界估計的連續漸近控制技術(即本文提出的PPAC控制器)，初始階段和穩態階段的最大跟蹤誤差分別為0.024 mm和0.067 mm，相比PPC初始階段跟蹤精度提高約11.1%，穩態階段跟蹤精度提高約40.2%，且隨著時間推移，控制誤差仍有下降趨勢。圖6給出了所選取預設性能函數與PPC、PPAC控制誤差的對照效果，可知控制誤差始終處于預設函數界內。另外圖6給出了匹配干擾和不匹配干擾的上界估計曲線，證明兩者是共存的，估計算法的收斂效果較好，在15 s左右趨于穩定，與之對應，隨著干擾上界估計的收斂，圖5中PPAC的穩態階段控制誤差較初始階段控制誤差明顯減小。

圖5 工況一跟蹤誤差對比Fig.5 Comparison of tracking errors for condition one

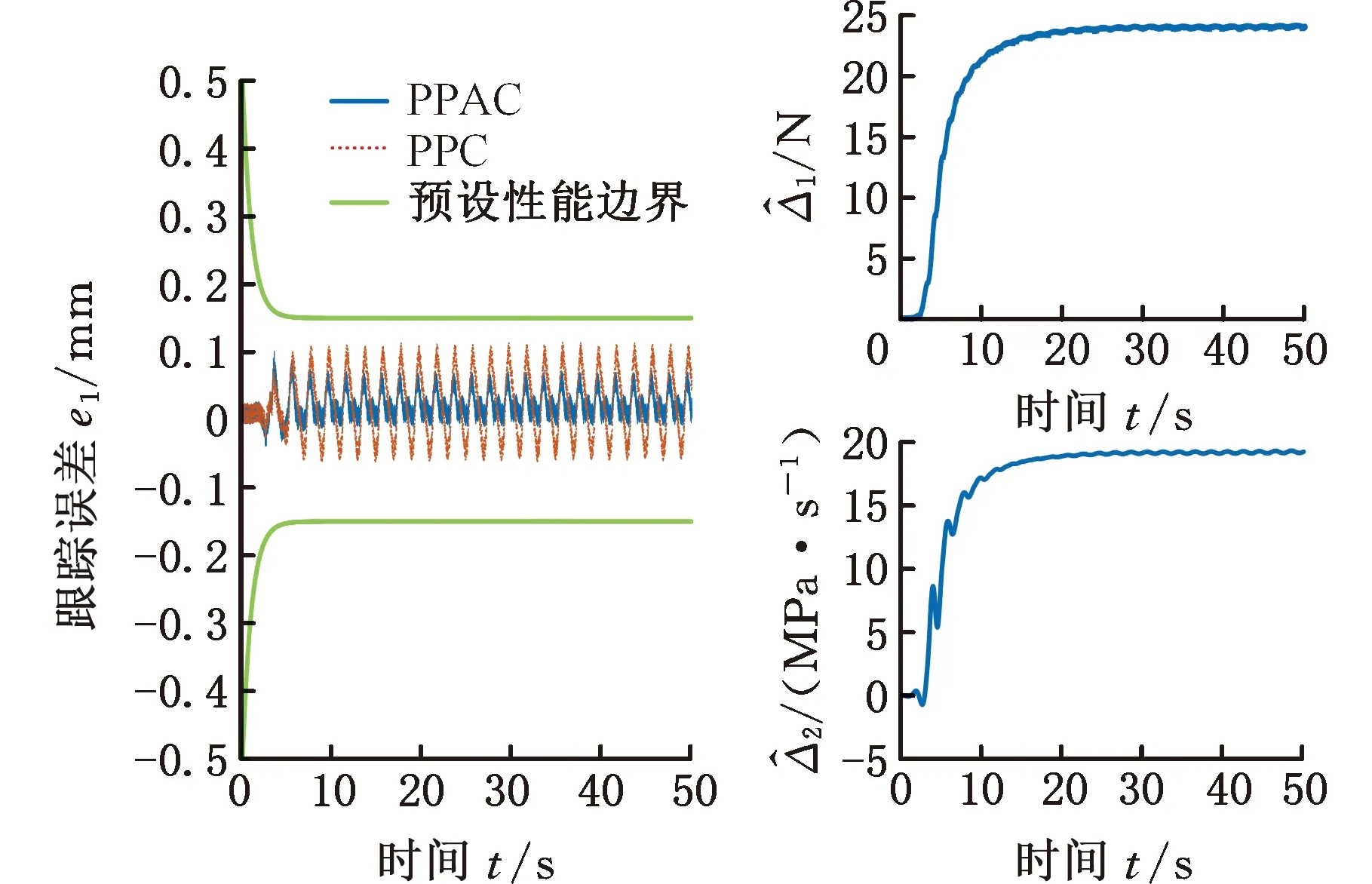
圖6 工況一預設性能效果和Fig.6 Effect of prescribed performance for condition

表 1 工況一最大跟蹤誤差emax

3.2 試驗工況二

圖7 工況二位置指令Fig.7 Command position for condition two

圖8 工況二跟蹤誤差對比Fig.8 Comparison of tracking errors for condition two

圖8為4種控制器作用下的跟蹤誤差對比曲線，另外計算了第一個運動周期和最后一個運動周期的最大跟蹤誤差emax，如表2所示(在工況一中，由于位置指令為經過光滑處理的正弦指令，初始階段較為平緩，因此選取兩個周期的數據進行對比)。顯然，FLC控制器相比于PID控制器，初始階段和穩定階段的最大跟蹤誤差分別由0.882 mm和0.932 mm減小至0.362 mm和0.354 mm。PPC控制器初始階段和穩態階段的最大跟蹤誤差分別為0.152 mm和0.149 mm，相比于PID和FLC控制器，初始階段跟蹤精度提高均超58%，穩態階段跟蹤精度提高均超57.9%。PPAC初始階段和穩態階段的最大跟蹤誤差分別為0.147 mm和0.085 mm，相比PPC初始階段跟蹤精度提高約3.2%，穩態階段跟蹤精度提高約42.9%。圖9給出所預設性能函數與PPC、PPAC控制誤差的對照效果，可知控制誤差始終處于預設函數界內。另外圖9給出了工況二下匹配干擾和不匹配干擾的估計曲線，收斂效果較好，在6 s左右趨于穩定，與圖8中PPAC的控制誤差收斂趨勢基本一致。

圖9 工況二預設性能效果和Fig.9 Effect of prescribed performance for condition

表2 工況二最大跟蹤誤差emax

以上兩種不同位置指令的跟蹤試驗均驗證了在本文所設計控制器的作用下，電液伺服系統具有較好的瞬態和穩態性能，通過對比4個控制器在初始階段和穩態階段最大跟蹤誤差，表明預設性能函數的引入可明顯改善瞬態性能，而基于干擾上界估計的連續漸近控制技術可進一步提升穩態階段控制性能。

4 結論

(1)本文提出了一種融合預設性能函數和基于干擾上界估計的連續漸近控制技術的電液伺服系統新型高精度控制策略，通過Lyapunov穩定性分析證明了控制器具有理論可預設瞬態性能和漸近穩態性能。

(2)選取了PID控制、反饋線性化控制和預設性能控制作為對比，通過兩種位置指令工況的跟蹤試驗，驗證了匹配干擾和不匹配干擾是共存的，而所提出控制器可很好地抑制匹配和不匹配干擾，在兩種試驗工況中，所設計控制器相比傳統PID控制和反饋線性化控制，初始階段跟蹤精度提高均超22.9%，相比于僅引入預設性能函數的控制器，穩態階段跟蹤精度提高超42.9%。