基于SIF均勻化方法的FGM板及FGM圓筒Ⅰ型裂紋尖端應力研究

李 戎，楊 萌，梁 斌

（河南科技大學土木工程學院，河南 洛陽 471023）

0 引 言

功能梯度材料（FGM）因其消除了傳統層壓復合材料結構中的界面問題，可在滿足工程結構輕量化需求的同時增強結構強度而被廣泛應用于航空航天、船舶和汽車制造等領域[1-3]。以汽車為例，車身噪音往往會伴隨實際行駛速度的持續提高而以幾何級數規律增加，共振有可能導致產生裂紋甚至結構破壞，對內燃機和氣缸套等關鍵FGM 零部件進行斷裂力學分析是保障整個車體結構穩定性和安全性的先決條件。

FGM 板和FGM 圓筒是工程機械關鍵零部件常見結構形式[4-5]。已有研究表明，含裂紋結構裂紋尖端應力值與構件斷裂韌性密切相關[6]。但是，由于裂紋尖端應力奇異性的存在，由有限元軟件得到的應力值不能直接用于工程設計中。因此，目前關于含裂紋FGM 結構的研究主要集中在應力強度因子（SIF）、斷裂韌性（臨界SIF）特性以及計算方法優化等方面[6-11]。Nazari 等[12]證明了功能梯度鋼的斷裂韌性取決于裂紋所在梯度區域的位置和方向。Sabuncuoglu等[13]利用位移相關方法（DCT）計算了FGM裂紋尖端附近SIF。陳建等[7]和Kim 等[8]則嘗試通過改進節點以及網格劃分方式等來優化SIF 計算方法。項目組前期研究結果顯示，含裂紋FGM 結構（板、圓筒）和對應含裂紋均勻材料結構的SIF之間存在與裂紋尖端應力值有關的比例關系，可基于此關系直接使用應力比值進行FGM 板SIF 均勻化轉換[14-16]。但是，這兩者之間裂紋尖端應力關系影響因素尚不明確，應力比值方面的研究在參考文獻中還未見涉及。

本文基于SIF 均勻化轉換方法，以含裂紋FGM 板和FGM 圓筒作為研究對象，構建FGM 結構和相應均勻材料結構之間裂紋尖端應力比值表達式，研究材料梯度、裂紋尺寸及其所在位置和構件幾何尺寸等因素對裂紋尖端應力比值的影響。

1 力學模型

基于有限元軟件MSC.Marc.2012 建立如圖1 所示的有限寬含邊緣裂紋平面應變板模型和含環向裂紋圓筒軸對稱模型，裂紋長度/深度為a，模型兩端施加相同拉力，L/W＞2，L/h＞2。模型材料分別選用FGM和均勻材料，FGM板和FGM圓筒的材料分別沿x方向以及r'方向按照指數函數連續變化。

2 理論推導

2.1 FGM板SIF的均勻化

圖2中給出了FGM 結構裂紋尖端幾何模型。對于FGM 板，其裂紋尖端附近應力場可表示為如下形式[17]：

其中，上角標P 代表FGM 板，r和θ為裂紋尖端極坐標，a為裂紋長度，KⅠ為Ⅰ型SIF。β是與結構兩側材料彈性模量比值有關的參數，FGM板左、右兩側材料性質沿x軸方向按照β連續性變化。E(x)為FGM 板彈性模量，FGM 板左側E(0)=E1，右側E(W)=E2。當E2/E1= 1 時，FGM 板退化為均勻材料板（*）。E(x)的表達式為

當θ= 0時，y軸方向應力可簡化為

FGM 和均勻材料裂紋尖端SIFKⅠ≠，但是應力奇異性不受材料梯度影響[24]，可利用“比值”形式消除應力奇異性。因此，當r→0，FGM板和均勻材料板的板寬、外部載荷和裂紋尖端附近網格劃分完全相同時，兩者裂紋尖端應力比值σy與相應SIF比值KⅠ/KⅠ*之間存在比例關系[14]

無量綱SIFFⅠ和SIFKⅠ滿足關系式FⅠ=KⅠ/(σhπa)，裂紋尖端應力σy和FⅠ之間存在如下比例關系式，可基于此式進行應力均勻化轉換。當FGM 板和均勻材料板裂紋尺寸相同a=a*時，(σy)P=FΙ/。

2.2 FGM圓筒SIF的均勻化

假定圖1中FGM 圓筒內、外表面材料性質沿厚度r'方向連續性變化，圓筒材料性質沿厚度方向按照冪指數函數變化（材料梯度指數p滿足0 ≤p≤∞）。基于線性混合法則[18]，FGM 圓筒彈性模量E(r')為

式中，下角標i代表內表面材料，下角標o代表外表面材料。根據線彈性斷裂力學，FGM 圓筒裂紋尖端應力場表達式為

上式中，上角標C 代表圓筒，KⅠ、KⅡ、KⅢ為SIF，(θ)、(θ)、(θ)為無量綱角函數，i、j=1、2、3對應空間坐標系的三個方向，Ⅰ、Ⅱ、Ⅲ分別表示三種裂紋形式，r和θ為裂紋尖端極坐標（見圖2）。圖1所示FGM圓柱殼所對應的Ⅰ型裂紋尖端應力場表達式為

材料梯度不影響應力奇異性以及無量綱角函數[20]。因此，當FGM圓筒和均勻材料圓筒（*）幾何尺寸、裂紋類型、外部載荷和裂紋尖端附近網格劃分完全相同時，兩者間裂紋尖端SIF和應力之間存在與裂紋尺寸有關的比例關系[15-16]，裂紋尖端應力比值可以進一步寫成如下形式：

當FGM 圓筒和均勻材料圓筒裂紋所在位置和尺寸均相同時，裂紋尖端應力比值和SIF比值相等，(σy/)C=FⅠ/。

對比公式（4）～（5）和（9）～（10）發現，FGM 板和FGM 圓筒結構形式不同，但是均可基于裂紋尖端應力比值實現SIF均勻化轉換，且轉換公式相同。

3 算例與討論

采用四節點四邊形單元建立如圖3～4 所示模型，裂紋尖端附近網格加密。板寬W=1 mm，圓筒壁厚h=1 mm，兩端施加拉力σh=1MPa。裂紋尖端附近最小網格尺寸emin大小參考文獻[14～16]，有限寬板emin=1/39mm，等厚圓筒emin=1/38mm。板和圓筒單元總數分別為29911和23 289，裂紋尖端附近單元數約為2萬個。設定泊松比為常數，ν=0.3；FGM 板左側材料彈性模量E1數值固定，FGM 圓筒外表面材料彈性模量Eo數值固定。

3.1 FGM板和均勻材料板之間Ⅰ型裂紋尖端應力關系

本文算例中，FGM板和相應均勻材料板裂紋尺寸相同。通過算例分析了材料梯度、幾何尺寸以及模型網格劃分等因素對裂紋尖端應力關系的影響。

3.1.1 裂紋尖端應力分布

由于裂紋尖端存在應力奇異性，使用Marc 得到的應力值隨模型網格尺寸改變而發生變化。由表1可知，FGM板和均勻材料板在幾何尺寸、網格劃分、裂紋尺寸a/W等完全相同的情況下，材料不同，裂紋尖端應力值不同；材料性質影響應力數值，但并不影響尖端附近應力分布規律；由于兩種板左側材料相同（E1=），FGM 板E2/E1=0.1，均勻材料板應力值σ*y均小于FGM 板應力值σy。當裂紋尖端附近最小網格尺寸emin小到一定程度（1/39mm）時，兩種板裂紋尖端應力比值恒定，不隨與尖端距離r/W的變化而發生改變（見圖5），此結論與文獻[14]相同。因此，下文中取用尖端第一個單元節點應力值進行分析。

表1 板裂紋尖端應力分布Tab.1 Stress distributions of crack tip in plate

3.1.2 應力比值影響因素分析

本文中，假定FGM 板由兩種材料混合而成，板中左、右兩側（x= 0,W）材料彈性模量比E2/E1反映FGM 材料組分變化，彈性模量E沿x軸方向按照材料梯度指數β=( 1/W)·ln(E2/E1)連續性變化，β= 0（E2/E1=1）時可退化為均勻材料板。圖6 中給出了FGM 板和相應均勻材料板裂紋尖端應力比值隨裂紋尺寸a/h和指數β變化的曲線圖。由圖6可見，在裂紋尺寸以及板寬一定的情況下，E2/E1不同，裂紋尖端應力比值不同；應力比值曲線變化幅度隨 |β|增大而變大，曲線形狀與β值有關。β＜0 時應力比值隨a/h的增大先增大后減小，曲線形狀開口向下，β＞0時曲線形狀開口向上。

結構裂紋尖端應力值與所處位置材料性質有關，裂紋尖端位置沿x軸方向隨裂紋尺寸a/h增大發生變化。為方便對照，圖7 給出了圖6 中FGM 板和均勻材料板裂紋尖端位置彈性模量比值E/E*變化曲線。結果顯示，σy/σy*與E/E*相互對應，曲線形狀基本相反，該現象反映了裂紋尖端應力值對材料彈性模量的高度依賴性。

3.2 FGM圓筒和均勻材料圓筒之間應力關系

3.2.1 外表面環向裂紋

外部載荷相同的情況下，含環向裂紋圓筒裂紋尖端應力受裂紋所在位置及尺寸、材料性質、構件幾何尺寸等因素影響。表2 和圖8 中針對外表面環向裂紋，分別給出了均勻材料圓筒和FGM 圓筒裂紋尖端應力分布表和應力比值變化曲線圖（內外半徑比Ri/Ro= 0.8）。表中，兩種圓筒外側材料相同（Eo=），FGM圓筒Eo/Ei=0.1。對比分析后發現，兩種圓筒裂紋尖端附近應力分布規律完全一致，但是應力值大小受圓筒材料性質控制。當圓筒裂紋尖端網格最小尺寸emin=1/38mm，裂紋尖端附近應力比值穩定、數值不隨與尖端距離r/h變化而發生改變，此結論與文獻[15]相同，下文同樣選取裂紋尖端第一個單元節點應力值進行分析。

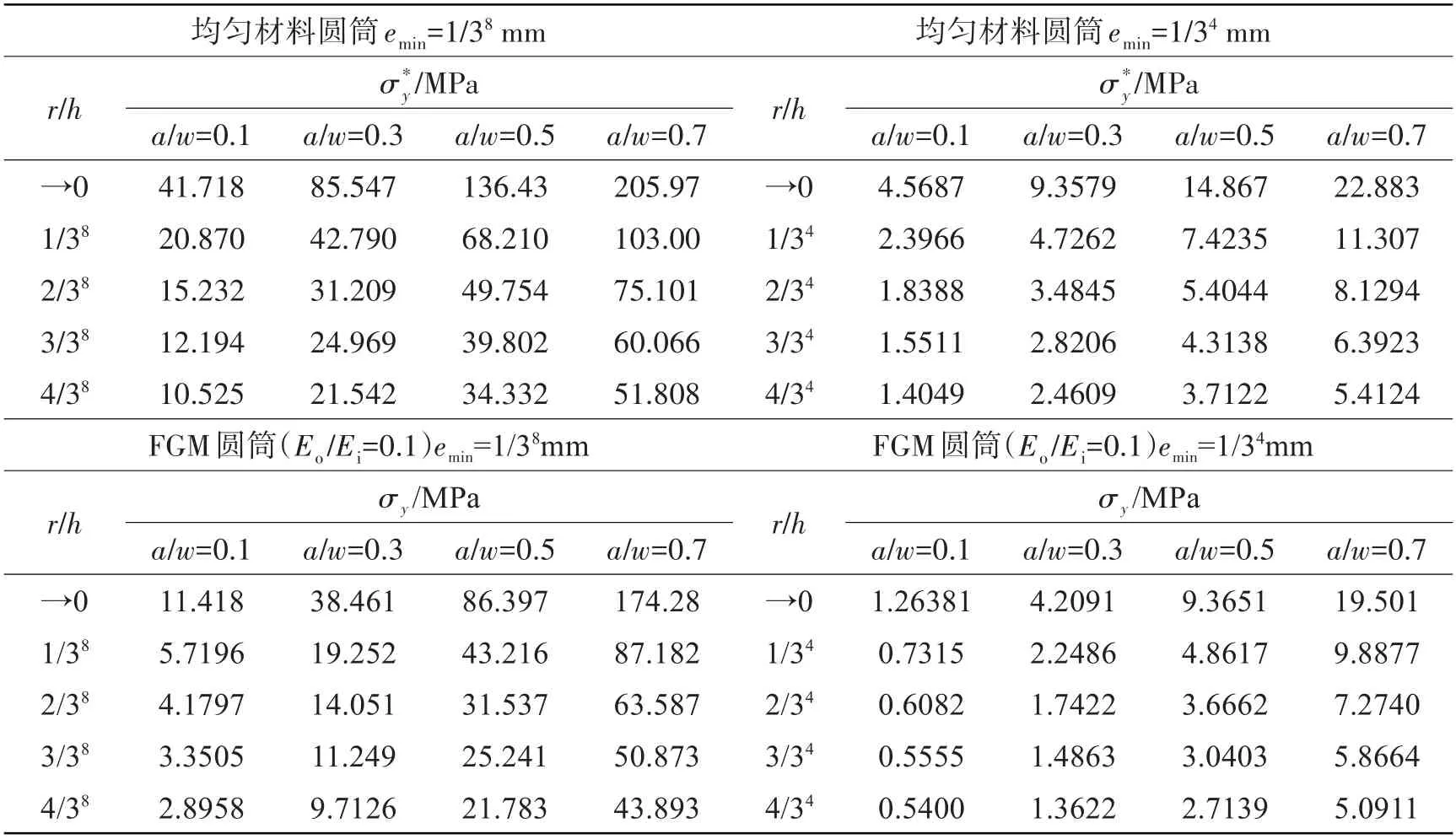
表2 含外表面環向裂紋圓筒裂紋尖端應力分布Tab.2 Stress distributions of crack tip in hollow cylinder with external circumferential crack

FGM 圓筒體積分數按照冪指數函數沿厚度方向連續變化，材料性質可由材料梯度指數p控制。圖9（a）和圖9（b）分別給出了裂紋尺寸a/h以及材料梯度指數p不同時FGM 圓筒和相應均勻材料圓筒裂紋尖端應力比值曲線變化圖（Ri/Ro=0.8）。由圖可知，圓筒內外表面材料彈性模量（Ei和Eo）差異越大，p對應力比值σy/的影響越顯著，Eo/Ei對σy/的影響主要體現在a/h較小的情況下；p＞5時，材料性質開始逐漸接近均勻材料狀態，材料梯度對σy/的影響減弱。圖10給出了圖9中圓筒裂紋尖端位置彈性模量比值E/E*曲線圖。可以看出，σy/變化規律與該位置對應E/E*變化規律相互對應，反映了應力對材料梯度的高度依賴。

材料梯度對圓筒裂紋尖端應力的影響程度與構件尺寸有關。圖11 給出了FGM 圓筒和對應均勻材料圓筒應力比值隨內外半徑比Ri/Ro變化的曲線圖。當材料梯度指數p＜0.1 或p＞5 時，FGM 大部分區域特性接近均勻材料特性。因此，下文中，取p= 1。

與美、英、法不同，俄羅斯保持一支龐大的常規動力潛艇艦隊，主要在沿海作戰，執行反艦任務。在政治上還被用于力量展示，曾使用“口徑”巡航導彈打擊敘利亞的目標。只有較新的潛艇可攜帶“口徑”導彈，但與更大的攻擊型和巡航導彈型核潛艇相比，常規潛艇的能力顯得非常有限。

由圖可知，內外側彈性模量比Eo/Ei對應力比值σy/的影響主要體現在Ri/Ro較小的情況下，影響程度隨著Ri/Ro改變而有所不同；Ri/Ro=0.1 時，Eo/Ei對σy/的影響隨裂紋尺寸a/h增大而增大；當Ri/Ro=0.9時，Eo/Ei對σy/的影響隨a/h增大先增大后減小。

3.2.2 內表面環向裂紋

結構尺寸、材料和外部載荷等均相同的情況下，裂紋尖端應力受裂紋所在位置影響。表3和圖12針對內表面環向裂紋，分別給出了均勻材料圓筒和FGM圓筒裂紋尖端應力分布表和兩者應力比值變化曲線圖（Ri/Ro= 0.8）。經過對比分析發現，兩種圓筒應力變化規律相同，應力值大小完全不同。對比表2 和表3 發現，裂紋所在位置直接影響應力值大小，但并未影響應力變化規律，此結論與文獻[16]的相同。

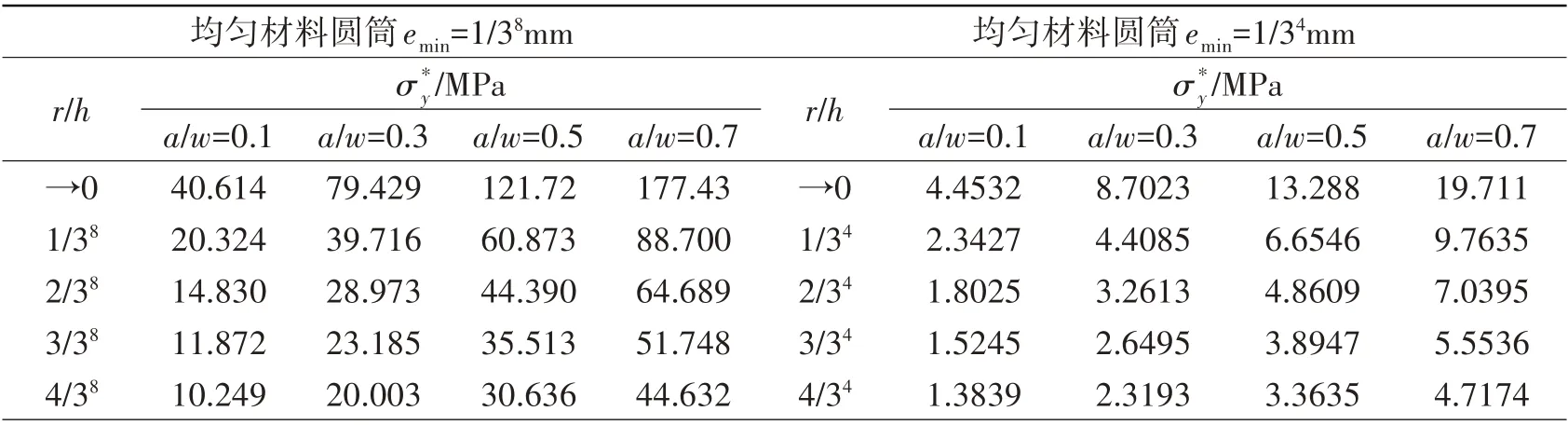
表3 含內表面環向裂紋圓筒裂紋尖端應力分布Tab.3 Crack tip stress distributions in hollow cylinder with internal circumferential crack

FGM圓筒（Eo/Ei=0.1）emin=1/38 mm FGM圓筒（Eo/Ei=0.1）emin=1/34 mm r/h→0 1/38 2/38 3/38 4/38 σy/MPa σy/MPa a/w=0.7 25.603 12.102 8.3640 6.2826 5.0752 a/w=0.1 75.765 37.903 27.649 22.128 19.096 a/w=0.3 142.24 71.096 51.848 41.473 35.766 a/w=0.5 193.38 96.670 70.463 56.345 48.584 a/w=0.7 233.24 116.53 84.944 67.914 58.542 r/h→0 1/34 2/34 3/34 4/34 a/w=0.1 8.2653 4.2485 3.2029 2.6517 2.3593 a/w=0.3 15.518 7.6241 5.4814 4.3146 3.6616 a/w=0.5 21.084 10.168 7.1699 5.5189 4.5781

對比圖8 和圖12 可見，當裂紋尖端附近最小網格尺寸小到一定程度（emin=1/38mm）時，應力比值σy/穩定，裂紋所在位置影響σy/數值及其變化規律。當裂紋位于圓筒內表面時，σy/隨裂紋尺寸a/h增大而減小；當裂紋位于圓筒外表面時，σy/隨a/h增大而減小。

圖13 給出了含內表面裂紋FGM 圓筒和相應均勻材料圓筒裂紋尖端應力比值σy/σ*y隨裂紋尺寸a/h以及材料性質Eo/Ei變化的曲線圖（Ri/Ro=0.8）。由圖可知，σy/σ*y隨Eo/Ei的增大而減小，材料組合對裂紋尖端應力的影響主要體現在a/h較小的情況下；圓筒內外側材料性質差別越大，p對σy/σ*y的影響越顯著。

圖14 中給出了圖13 所示圓筒裂紋尖端位置對應的彈性模量比值E/E*曲線圖。將兩圖進行對比后發現，σy/與E/E*的變化規律高度相似，此現象同樣反映了應力值對材料梯度的高度依賴。

4 結 論

本文針對工程常見的含裂紋FGM 結構，基于均勻化轉換方法，探討了材料梯度性質、裂紋參數、構件幾何尺寸等因素對裂紋尖端應力比值的影響，主要結論如下：

（1）FGM 板和FGM 圓筒結構形式不同，但是均可僅基于裂紋尖端應力比值直接實現SIF 均勻化轉換，并且應力均勻化轉換公式相同。

（2）外部載荷相同的情況下，含邊緣裂紋FGM 結構（板、圓筒）和相應含裂紋均勻材料結構裂紋尖端應力分布情況相同，但是應力值和兩者之間應力比值受材料性質、結構尺寸以及裂紋所處位置等因素影響。應力值均隨裂紋尺寸增大而增大；應力值和應力比值與裂紋尖端彈性模量變化規律相互對應，數值隨裂紋尖端所在位置材料性質而變化；裂紋尺寸以及材料性質一定的情況下，圓筒內表面裂紋應力比值大于外表面裂紋應力比值。

（3）FGM 板和FGM 圓筒材料性質可由材料梯度控制。而裂紋尖端應力不僅與材料組合有關，還受裂紋所在位置影響，裂紋尖端應力比值σy/變化規律和尖端位置彈性模量比值E/E*變化規律相對應。以圓筒為例（取梯度指數p= 1），外表面裂紋下，σy/隨圓筒兩側彈性模量比值Eo/Ei增大而增大，E/E*隨Eo/Ei增大而減小；內表面裂紋下，兩者均隨Eo/Ei增大而減小。

（4）材料梯度對FGM 圓筒和相應均勻材料圓筒之間裂紋尖端應力比值σy/的影響程度受圓筒內外半徑比Ri/Ro影響，影響程度隨Ri/Ro改變而發生變化；內外側彈性模量比Eo/Ei對σy/的影響主要體現在Ri/Ro較小的情況下。