盾構螺旋機葉片截面形狀對其耐磨性的影響

0 引言

1 理論基礎與模型假設

根據參考文獻[1]的分析，盾構螺旋機的磨損最主要是磨粒磨損。同時針對磨粒磨損的分析采用拉賓諾維奇模型及其公式，見圖1所示。

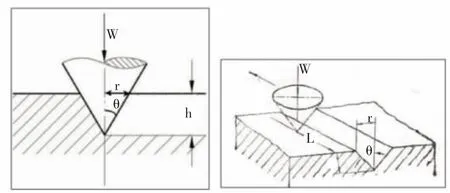
圖1 拉賓諾維奇磨粒磨損模型圖

為更便于量化，假設葉片截面為L型，其各處尺寸見圖2所示。其中，設啄=a×啄。考慮到啄1為支撐結構及抵抗土體磨損的最小厚度，此值在設計初期，將根據結構的受力計算得出啄1的最佳值，因此我們可以設啄1為定值常量。再根據拉賓諾維奇提出的磨損微觀模型及磨損量計算公式，求出a的最佳比例值。

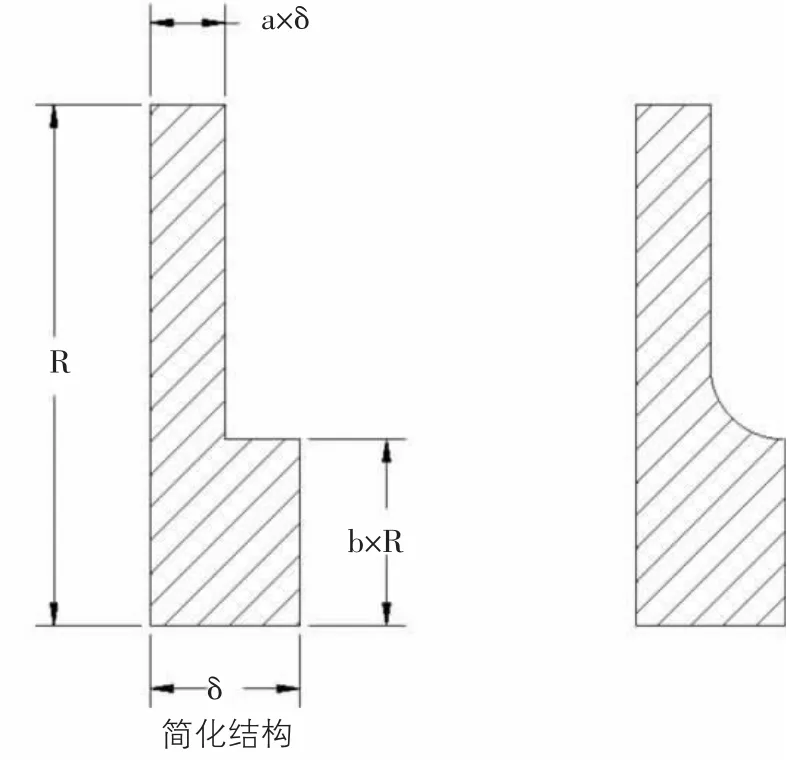
圖2 L型葉片截面尺寸圖

為便于問題分析、簡化計算，進一步做以下假設：①各種磨損均為磨粒磨損；②螺旋機葉片的重量是厚密度與葉片當量厚度的乘積；③由于實際應用中一般葉片與筒體選用的耐磨材料相同，同時葉片與筒體之間的作用是相互的，所以這里假設葉片與筒體的磨損系數和耐磨硬度是相同的。④由于研究的是葉片厚度與螺旋機磨損量的關系，螺旋機的其它性能參數均作為定量考慮。例如筒徑、節距、材質等均為定值。

2 公式推導與計算

根據磨粒磨損顯微切削模型，葉片與筒體之間的磨損量可以由下面公式計算得出。

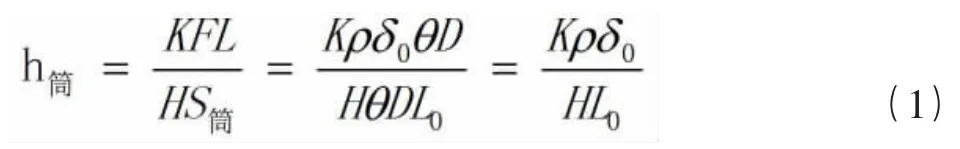
其中h為筒體厚度磨損量；

K為綜合磨損系數；

云銅總廠研發中心利用工業鹽在高氯體系下實現了鉛、銻、鉍的定向分離[1]，在液固比為L∶S=7∶1、溫度80 ℃、時間2 h、NaCl濃度為6 mol/L的條件下，鉛的脫除率為89.63%，銻的脫除率為13.97%，鉍的脫除率為26.67%。雖然實現了大部分鉛的分離，但該體系下金、銀也存在一定的分散，回收難度較大。

L為筒體受葉片重力區域長度；

δ為葉片截面的當量厚度；

ρ為葉片的厚密度；

H為葉片耐磨材料的硬度。

其中h為葉片徑向磨損量；

D為筒體內徑；

θ為筒體底部與葉片接觸的角度；

δ為葉片摩擦面的當量寬度；

P為螺旋機葉片節距。

考慮到螺旋機的輸送能力，單位輸送量下磨損量對實際應用更有意義。所以我們用式（4）來考量磨損量的多少。x為h與h在磨損量考量中所占的比重。由于筒體的厚度相對于葉片半徑較小，且磨穿筒體后，螺旋機將無法正常工作。所以x一般取小于1的數值。

根據螺旋輸送機輸送能力公式：

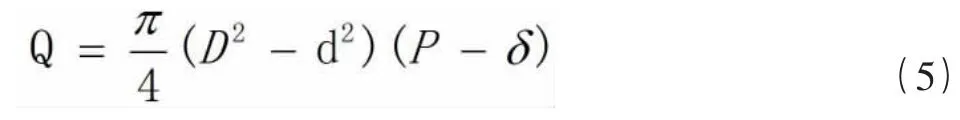
將公式（5）、（1）、（2）、（3）代入公式（4）得：

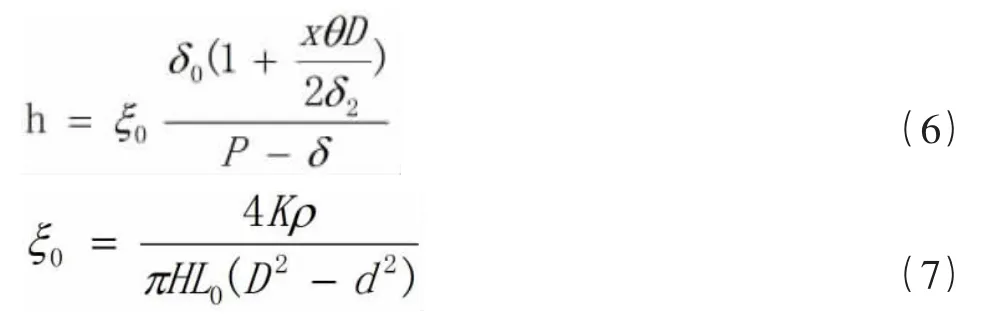
將h對a求導并取0得：

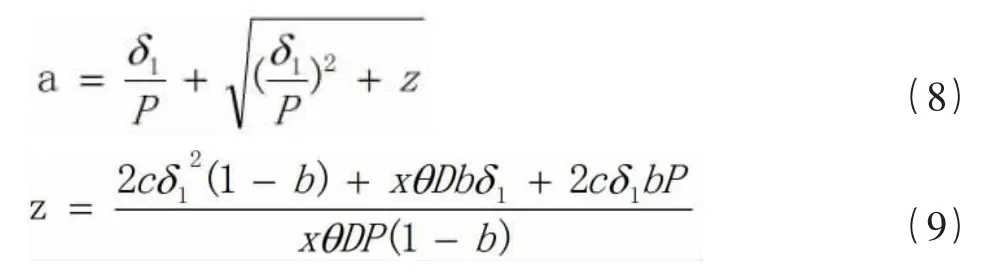
經過數值驗證，a為此數值時h是最小值。將常用直徑螺旋機的各項參數代入式（8）中，同時x值取0.5時得a值如表1所示。

表1 不同直徑與葉片厚度情況下計算出的a值

市場上流行的幾家進口品牌盾構機的實際螺旋輸送機的葉片厚度與外周耐磨塊的厚度值參見表2。

表2 不同直徑、廠家葉片厚度數值

通過表1和表2中的a值對比看，上述磨損模型和計算公式的結果與現在主流盾構機廠家的螺旋機葉片設計尺寸非常接近。證明本文中的理論計算與實踐積累是符合的。我們也可以進一步通過實際案例，來對比查看螺旋機的磨損位置和磨損情況與本文假設模型是否一致。

3 實際案例對比

本文這里從市面常用盾構機中取一些具有代表性的幾種機型，分別對比他們在使用中的摩擦位置以及截面形狀與本文上訴假設模型是否符合。進而驗證假設模型及其計算出的比例值是否正確。

如圖3所示為某900直徑的螺旋機葉片，其采用的方案是在葉片外周焊接高耐磨材質的耐磨塊。耐磨塊的寬度比葉片本體寬，其寬度比例值a=0.6，參見圖4。同時在葉片表面的外周方向上增加了耐磨焊，從而補強磨損較重區域的耐磨性。耐磨塊的寬度與葉片寬度比例值與本文的公式結果是相符合的。同時耐磨焊的位置的選擇，也與本文的磨損假設模型保持一致。

圖3 某900直徑螺旋機葉片圖

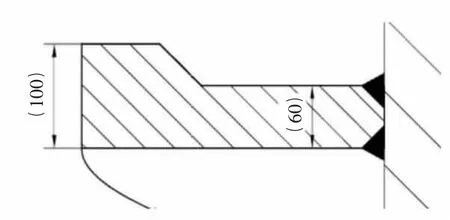
圖4 某900直徑螺旋機葉片截面尺寸圖

經過施工掘進后，磨損后的螺旋機葉片的照片見圖5。不難看出，通過施工后磨損情況的照片，我們可以看到螺旋機下葉扇片的磨損較輕，上葉扇片的磨損略重一些。葉片徑向外周的磨損最為嚴重。這個與上述假設模型也保持了一致。

圖5 某900直徑螺旋機葉片磨損情況圖

如圖6所示為某800直徑的螺旋機葉片，其采用的方案是在葉片外周布置螺栓固定的耐磨塊，針對磨損嚴重的區域采用了可拆換式設計，為施工的維護保養以及日后的修補提供了方便。

圖6 某800直徑螺旋機葉片圖

在耐磨設計方面，其在葉片本體的徑向外周焊接耐磨焊，保護的區域與前述900直徑機是一樣的。這個與本文的磨損模型分析結果也是一致的。厚度的比例值是0.54，與本文的結論公式也是相符合的。圖7為某800直徑螺旋機葉片截面圖。

圖7 某800直徑螺旋機葉片截面圖

經過施工后，螺旋機的磨損情況照片見圖8。可以看出，螺旋機葉片的磨損程度的順序依然是葉片徑向外周最強，其次是上葉扇片，最輕是下葉扇片。這個與前述機型的實際情況一樣，同時也與本文的磨損模型保持一致。

圖8 某800直徑螺旋機葉片磨損情況圖

該可拆卸耐磨塊對葉片本體鋼結構產生了有效保護，本體鋼結構磨損量并不大，在后續的維修改造中仍可繼續使用。但由于耐磨塊的連接部位被泥土填塞嚴重，后期的更換可操作性并不大。同時，由于是螺栓連接，遇到較大撞擊外力時耐磨塊會較易脫落，雖然案例中只有極個別脫落現象，但這依然是不可忽略的問題。

4 結論

由于螺旋機在施工中的重要性，現階段其葉片設計越來越傾向于更大更重方向發展。這與理論上的最優化設計不相符。螺旋機葉片厚度的設計也并非越厚越好。本文根據磨粒磨損顯微切削模型，推導出公式（8）作為“L”型螺旋機葉片寬度比例的理論最佳值，為設計提供了理論支持。同時，根據實際案例的葉片設計和磨損情況，驗證了該模型的可行和正確。可以在后續的設計中參考使用。

另外因磨損系數與很多因素有關，單憑計算很難得到具體數值。所以本文只是按照理論計算尋找最優值，未考慮最優值與其他值的磨損偏差量。若能用實驗測得各種地質對某種耐磨材質的磨損系數，將可以優化計算公式且更深入分析葉片截面形狀和厚度對螺旋機耐磨性能的影響。基于以上的不足，也希望本文能夠拋磚引玉，希望后續能有更多的單位和個人參與到盾構螺旋機磨損的研究中，測試出磨損試驗的數據或引進更先進和專業的理論模型對其進行分析，從而推動盾構機制造行業的發展。