扭切式鼻坎挑射水流作用機理分析

吳錦鋼，邱 勇，周鑫宇，葛亞飛，黃梓涵

(云南農業大學水利學院，云南 昆明 650201)

0 引 言

泄水建筑物末端挑坎體型的選擇是水利水電工程中消能防沖設計中的關鍵問題[1]。隨著水利工程開發條件日趨復雜，傳統的連續式鼻坎難以滿足工程布置要求，需要在此基礎上對體型作出相應的修改或者優化，得到能夠改變出坎水舌空間形態或水股落點位置的異型鼻坎[2]。為此，許多學者在鼻坎體型選擇以及水力特性研究方面做了大量的工作。練繼建等[3]以提高消能率和減輕霧化現象為目的，探究了水舌在平面上對稱橫向擴散的舌型挑坎與連續坎水舌的液滴粒徑與下游降雨強度分布規律；孫穎等[4]為防止下泄水流沖刷河岸，采用雙曲型挑坎，使得出坎水舌在對沖后仍沿對稱軸線方向擴散；Deng等[5]在針對大流量、窄河谷需要將水舌縱向拉伸情況下，優化出一種新型窄縫挑坎，結合數值模擬和模型試驗，研究了水舌形態的形成機理；劉昉等[6]采用正交試驗，對研究了扭曲式鼻坎中的參數變化對出坎水舌和下游河床的敏感性分析。

針對狹窄彎曲型河谷布置泄水建筑物，文獻[7- 8]依托水工模型試驗成果，采用扭切式挑流鼻坎，通過邊墻的偏折，迫使水舌在平面上轉向，給出了出坎水舌形態及水股落點，解決了水流平順歸河問題。本文采用連續性方程、動量方程、彎道超高經驗公式結合沖擊波理論，對扭切式鼻坎挑射水流作用機理進行分析，研究鼻坎內軸線立面挑射水流的水深和流速沿程變化規律、邊墻偏轉側平面偏折水流水面超高經驗公式以及底部斜射水流在出坎處的出射偏折角度。

1 反弧鼻坎水流結構分區

根據水工模型試驗[7- 8]和數值模擬成果[9]，扭切式鼻坎水流出坎后能夠在空間上形成大面積的拉開，同時促使水股平面偏折，運動較為復雜。本文結合反弧段挑坎水流運動狀態(見圖1)的不同，將其概化為立面挑射水流、平面偏折水流和底部斜射水流[9]，選取微元體進行受力分析。

圖1 反弧段出坎水流平面形態

2 立面挑射水流

軸線附近直線前行的水流進入挑坎段后，水面沿反弧底板不斷爬升、水深增加、流速降低。

2.1 連續方程

假定水流在軸線橫向上呈均勻分布[10]，流速分布沿水深滿足冪指數分布規律[11]，則水流的連續方程為

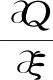
(1)

式中，Q為流量；ve為沿微元體法向距離鼻坎底部高度z的流速，m/s；v0為水流表面的速度，m/s；H為鼻坎內水流深度，m；m為冪指數的次數。

忽略指數m的沿程分布變化，連續方程可化簡為

(2)

2.2 動量方程

選取反弧段鼻坎水流作為控制體，如圖2所示，通過動量方程推求沿軸線方向的反弧段水流沿程水深和流速。

圖2 反弧段動量方程控制體

將動量變化量和外力作用項分別代入等式兩邊，得到

(3)

(4)

等式右側，由于壓強P沿程變化，其表達式仍需推導，同時假定水流流線沿水深分布均勻且不考慮水流在行進過程中邊壁對水體產生的摩阻力[14]。

2.2.1 反弧段動水壓強沿程分布

在上述反弧段上任取一段水深為H、長度為ds、高度為dh的單寬微元體，微元體軸線距離反弧段曲面底部高度為h，如圖3所示。

圖3 動水壓強微元體示意

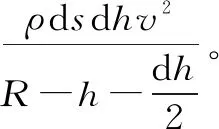
根據牛頓第二定律，微元體沿軸線的運動方程，可表示為

(5)

式中，ρ為水的密度，kg/m3；g為重力加速度，m/s2；R為反弧段結構半徑，m；v為水流速度，m/s。

對于常數C，由邊界條件(h=R-H)時，P=0，解出C=-ρv2lnH-pg(R-H)cosα，將C代入式(5)，整理后得到反弧段動水壓強沿程分布表達式，即

(6)

2.2.2 反弧段沿程水深和流速

基于上述分析，將式(4)、式(6)帶入式(3)中，整理化簡后得

(7)

(8)

式(2)和式(8)構成反弧段封閉方程組，即

在此基礎上，利用龍格-庫塔法[15]，可以求得反弧段的沿程水深H及流速變化v0。

基于該封閉方程組，結合挑流消能公式[16]，可進一步計算出軸線附近的立面挑射水流挑距。

3 平面偏折水流

扭切式挑流鼻坎的一側邊墻以弧形向軸線方向偏轉，上游端與邊墻相切，下游端與反弧段末端軸線相接，其特殊體型使得水流結構發生變化，出坎水舌在平面上發生橫向偏轉[7]，從而影響水舌落點的分布。

圖4 彎道環流條形水體

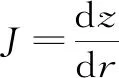
(9)

式中，v為水流速度，m/s；r為左側圓弧邊墻的半徑，m；B為鼻坎寬度，m。

彎道超高計算公式(9)在絕大多數情況下，其底坡為平坡或坡度很小，而扭切式鼻坎的底板曲率較大，水流爬升效應明顯[18]，對于超高的影響不能忽略。

考慮底板曲率的影響，計算該計算點(見圖5)與前一點的高差Δz，Δz=R(cosα1-cosα2)。

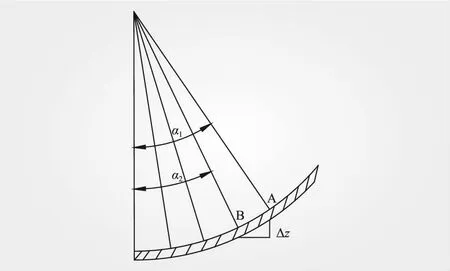
圖5 反弧段等分

由于底板曲率的存在，使得爬升的水流超高值遠低于底板為平坡時的數值[19]。若想要計算某一點的超高值，可將彎道超高理論計算值ΔH乘以這一點與等分后前一點的高差Δz。考慮到高差Δz帶來的計算誤差，引入一個調整系數k(反應底板曲率沿程對于超高計算的影響，則底板為曲面時該點的超高值可表示為

ΔZ=ΔkH×Δz

(10)

式中，k為調整系數，經試驗率定，取值范圍0.5～1.2。

根據式(10)計算結果，考慮相應安全超高，可以確定反弧段邊墻高度。

4 底部斜射水流

泄槽水流進入挑坎段后，受弧形邊墻的影響，水流沿邊墻運動的同時，在邊墻起始位置產生斜偏右方向的擾動水流。偏折水流如圖6所示，將其運動方向分解為順溢洪道軸線方向v′x和垂直于溢洪道軸線方向v′y。當沿軸線運動的慣性水流受到垂直于溢洪道軸線方向的水流擠壓作用后，導致其運動向弧形邊墻的另外一側偏斜，偏斜水流運動至挑坎一側后，在圓弧鼻坎出流處的水舌與軸線呈一小角度出射。

圖6 偏折水流平面示意

直線邊墻可采用IPEEN沖擊波理論[20]計算擾動線的波角，而對于一側邊墻曲線型偏折，可看成是無數直線邊墻的連續微偏折[21]。若直接將偏折處起點與終點相連接，誤差將會偏大，于是作起點與終點連線的中垂線，中垂線延長至圓弧形成交點，連接起點與交點，形成新的直線邊墻來代替圓弧邊墻，再依次作中垂線，以無限逼近圓弧邊墻。

將圓弧邊墻作一次中垂線，把起點與交點相連的形成的邊墻稱為“直線邊墻”，其與左側直線邊墻的角度為γ，擾動線與直線邊墻的夾角β可采用下式計算為[22]

(11)

式中，Fr為偏折起點處水流弗勞德數。

水流在曲線型邊墻的導向作用下，能量損失較小，擾動水流速度對偏折前的流速具有繼承性[22]。將擾動水流速度分解，由幾何關系有，沿y方向速度矢量v′y為

v′y=v×cos(90°-β-γ)

(12)

當沿軸線運動的慣性水流速度矢量vx(v′x)與邊墻偏轉所產生的垂向流速矢量vy合成后(忽略v′y沿y方向的速度衰減[23]，即v′y與vy近似相等)，軸線方向的慣性水流運動方向改變，斜向出挑，相撞擊后的水流與溢洪道軸線的夾角θ為

(13)

通過值的計算θ值，可確定圓弧邊墻對側需要截斷的邊墻長度，以避免底部斜射水流出現水面沿邊墻的壅高，影響水流挑射。

5 工程應用

某實際工程泄水建筑物出口軸線與河道交角過大，采用扭切式鼻坎挑流消將水舌平順引入河道，挑坎反弧半徑R1=10 m，挑射角度從左至右由25°漸變至57°41′50.230 6″，左側圓弧邊墻半徑R2=12 m，消能防沖工況下下游消能防沖洪水標準為30年一遇(P=3.33%)，泄洪洞相應下泄流量71.96 m3/s。

采用上述方法分別對泄槽軸線立面挑射水流水面線和流速分布、平面偏折水流超高進行驗證，結果如圖7～9所示。

圖7 反弧段軸線沿程速度對比

圖8 反弧段軸線沿程水深對比

圖9 偏轉邊墻水面爬升對比

由圖7～9可知，根據連續性方程、動量方程和彎道超高經驗公式，結合沖擊波理論進行機理分析，所得到的坎內軸線立面挑射水流的水深、流速沿程變化公式以及邊墻偏轉側平面偏折水流水面超高公式計算結果和試驗研究成果誤差均不超過10%。此外，底部偏折出挑水流的偏斜角度公式計算值為8.9°，與試驗所得6.8°基本吻合。

6 結 語

本文結合水工模型試驗和數值模擬所展現的扭切式鼻坎出坎水舌空間形態，將鼻坎內的水流分成立面挑射水流、平面偏折水流以及底部斜射水流三部分水流，結合其受力特點，采用連續性方程、動量方程、彎道超高經驗公式結合沖擊波理論，分別對水流作用機理進行了分析，可以得到：

(1)對于軸線附近的立面挑射水流，綜合應用連續性方程與動量方程分析其坎內沿程水深與流速的變化，進而求得挑距。

(2)對于圓弧邊墻處的平面偏折水流，基于彎道環流原理，利用經典的彎道超高公式，推導出底板為曲面時的超高值經驗公式。

(3)對于圓弧邊墻另一側的底部偏折水流，基于沖擊波理論，得到了扭切式鼻坎底部偏折出射水流與軸線夾角的經驗公式，可為狹窄轉彎河道挑流消能工程設計提供一定指導。