雷達大下視角下地雜波特性分析

高 希 杜 勇 高曉明

(西安電子工程研究所 西安 710100)

0 引言

在歷次戰爭中，制導武器逐漸成為戰場上的焦點，發揮著至關重要的作用。而雷達能夠在一定空域內搜索、識別和跟蹤目標，常用于導彈制導系統，尤其是主動雷達可不分天氣和時間，在較遠距離處發現目標，廣泛應用于諸多導彈系統中。但是雷達在打擊目標過程中，除了會接收到目標信號外，還會接收到幅度高于目標的雜波信號，而且雜波復雜多變，易受環境因素的影響，如地形、風速等等，這些都嚴重影響著雷達的目標檢測性能。

在早期研究中，由于距離分辨率過低，且在低下視角情況下，分辨單元內存在大量獨立的隨機散射點，但沒有起支配作用的強散射點，此時認為雜波滿足瑞利分布。但是在實際場景中，毫米波雷達由于分辨率提升，其接收到的雜波特性會由于載體平臺姿態改變而變化，文獻[2]研究了導彈俯沖飛行時非正側視雷達下雜波的空時耦合關系，得出導彈在俯沖運動時帶來的垂直速度分量會造成多普勒頻移與距離相耦合的結論。文獻[3]對導彈平飛和俯沖運動時的雜波空時耦合關系也進行了研究，得出相同的結論。

為研究大下視角下地雜波的特性，本文采用假設檢驗、分布擬合等方法對某毫米波雷達在大下視角下采集的實測地雜波數據進行分析，分析其分布特性，并對其相關性進行了研究，為后續大下視角下雜波抑制算法的研究提供了理論支撐。

1 雜波特性分析方法

雜波分布的研究從瑞利分布開始，隨著雷達分辨率的不斷提高，許多強散射點被分辨出來，雜波回波出現較大的拖尾效應，此時不再適合使用瑞利分布來描述雜波。于是，Geroge提出并使用對數-正態分布來擬合雜波的幅度特性，且取得了良好的擬合效果。但是由于對數-正態分布的拖尾過長，已不再適合描述瑞利和對數-正態分布之間的雜波，因此Sekine 等人提出了韋布爾分布模型來描述這部分雜波。幅度服從韋布爾分布的模型使用范圍較廣，適合描述地雜波、海雜波、氣象雜波等。隨著電磁理論的發展，Jackman通過研究雜波散射機理，得出了 K 分布模型，并對實測數據作擬合分析。K 分布模型在很大程度上反映了雜波的特性，且與實測數據具有良好的吻合性，因此成為雜波常用的分布模型。

這些常用分布的得出既需要通過理論推導，也需要經過實測新數據的驗證，而通常需要對實測數據進行以下分析：相關性、時頻特性，并使用幅度分布擬合以及假設檢驗的方法對雜波數據的幅度特性進行分析。

1.1 相關性分析

在時間和空間上，雜波具有一定的關聯性，分別稱為時間相關性以及空間相關性。其中，時間相關性通常指雜波在同一距離單元通過慢時間積累所展現出來的關聯性；而空間相關性指單個快時間內不同距離以及方位單元之間的雜波所展現的關聯特性。通過研究雜波的時間相關性和空間相關性，可以研究針對某一地形地貌和相關性來產生服從某一分布的雜波背景，以及在該背景下的雜波抑制和目標檢測的算法。

1.2 幅度分布擬合

為了驗證雜波數據到底服從經典模型中的哪一種分布模型，需要對雜波數據的幅度進行統計，畫出對應的直方圖。同時也分別畫出與雜波數據具有相同統計特性(分布參數，特征矩)的理論模型的概率密度函數(Probability Density Function，PDF)，包括高斯分布、瑞利分布、對數正態分布、韋布爾分布、K分布。另外，也可從累積分布函數(Cumulative Distribution Function，CDF)出發，統計雜波數據和經典分布的CDF，來進一步說明雜波數據的幅度分布特性。

各種分布的統計特性，如分布參數，可通過最大似然估計法估計雜波參數得到，或者通過計算雜波數據的一階矩和二階矩得到，具體如表1所示。

表1 各分布模型的參數估計

1.3 假設檢驗

通過以上操作，我們只是粗略地選擇出了所需雜波符合的概率分布模型，并對雜波模型的參數進行了估計，但沒有進行深入的檢驗分析，因此需要檢驗模擬數據與理論模型是否一致或假設的分布與實測數據是否貼合。一般分析包括定性分析和定量分析，定性分析可使用直方圖或概率密度圖將擬合數據和理論模型進行直接對比；而定量分析則在一定假設條件下，計算擬合數據與理論模型的差距來直觀對比，常用的方法有χ檢驗和K-S(Kolmogorov-Smirnov)檢驗。

131 χ檢驗

作為一種評判數據擬合優良度的檢測方法，檢驗的檢測性能通常被認為是介于質量函數或密度函數與直方圖之間。檢驗既適應于連續分布，也適應于離散分布，在檢測過程中都要對檢驗的統計量進行計算。首先，假設擬合分布的取值范圍為[,)，我們將取值范圍等間隔劃分為個小區間，即[,)、[,)、…[-1,)，其中=，=，且可能取值=-∞，可能取值=+∞。然后，在連續情況下，使用預測分布的密度函數()計算，即

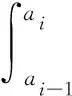
(1)

而在離散情況下，的計算公式為

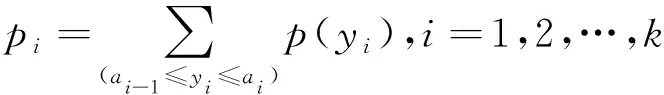
(2)

其中()是質量函數。

如果定義一組觀測樣本為,,…,，而為零假設，即假設是一組隨機變量，獨立同分布，且服從()，()是預測分布的密度函數。同時規定為檢測水平，那么可通過以下步驟進行檢驗：

1)統計出現在個區間的觀測值個數，設其數目為，=1,2,…,；

2)對預測分布的觀測值按概率出現在各個區間內的期望個數，=1,2,…,進行計算；

3)計算檢驗的統計值為

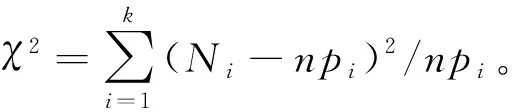
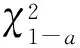
(3)

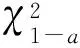
檢驗過程中最為關鍵的一點是確定變量的取值范圍，即區間。目前，還沒有一個明確的方法來選擇區間，并對所有的預測分布和樣本都有良好的效果。但是仍然可以通過以下原則來對區間進行選擇：首先，一般盡可能選擇使概率接近于相等的區間，最好情況下使每個區間的都相等。這樣做可以讓檢驗更加公平，只有當假設中的真實成分少于虛假成分時，才將其拒絕。其次，選擇的區間應使期望的值保持在一定范圍，一般≥5。此外，區間的數目應該在30或40以下。

132-檢驗

K-S(Kolmogorov-Smirnov)檢驗也可以用來檢驗數據擬合的優良度，但它通過比較擬合分布函數()與由樣本數據值定義的經驗分布函數來評估擬合的優良度。在K-S 檢驗過程中，我們并不需要對樣本數據以任何方式進行重組，也就意味著不用再劃分區間，也就沒有了信息的損失。另外，K-S 檢驗還有一個特點，它對樣本數據的數目沒有限制。

在計算K-S檢驗的統計量之前，我們必須確定經驗分布函數()。假設樣本數據為,,……，那么經驗分布函數()可定義為

(4)

對于所有實數，()是一個右連續的階梯函數。若()是預測的分布函數，那么數據擬合優良度的評價方法可通過檢驗()和()之間的相似度來完成。若用來表示K-S檢驗的統計量，其數值反比于擬合優良度，即當越大時擬合優良度越差。當超過某一個限制點,1-(是顯著水平，,1-為分位點)，就認為檢驗的零假設是錯誤的，而,1-的大小與假定的分布類型有關。

2 實測數據分析

采集毫米波雷達在大下視角情況下遭遇的地雜波數據作為實測數據，對其中第100幀和第280幀數據進行分析，先對其進行預處理，包括解包和脈沖壓縮，脈沖壓縮結果如圖1所示，左側為第100幀數據，右側為第280幀數據。

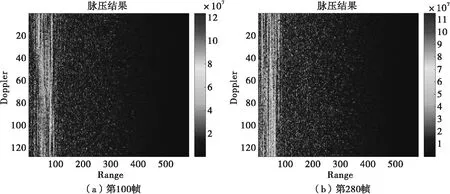
圖1 兩幀數據脈壓結果

采用動目標檢測(MTD)對兩幀數據的脈壓結果進行分析，得到圖3的結果。很明顯，由于導彈速度與空間的耦合效應，與靜止狀態和低下視角下的地雜波相比，大下視角下的地雜波表現為一條斜線。雜波的頻譜更寬，不同距離單元的雜波占據的多普勒通道不同，雜波的情況更為復雜，傳統通過估計雜波中心去雜波的方法不再適用，雜波抑制的難度加大。

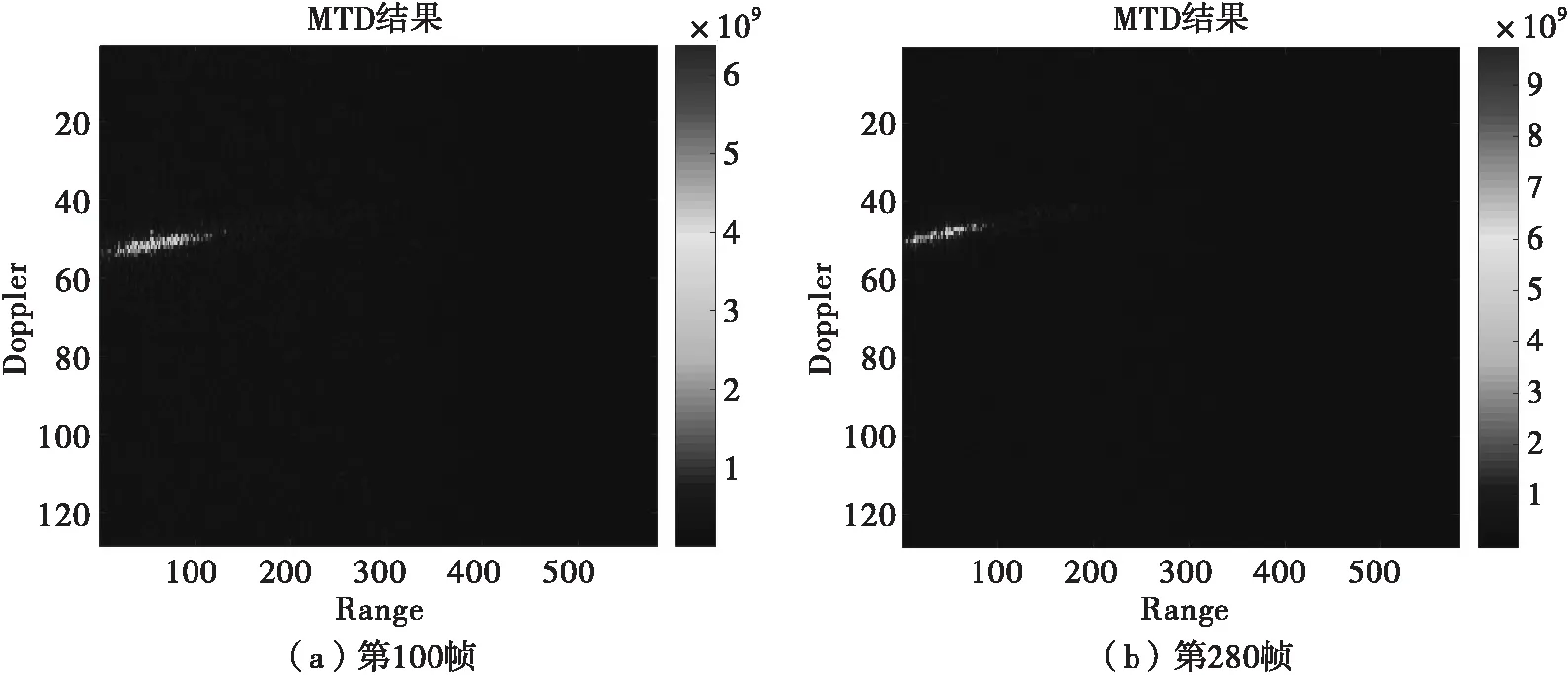
圖2 兩幀數據MTD結果

對這兩幀數據進行PDF和CDF擬合，得到圖3和圖4的擬合結果。可以看出，大下視角下地雜波與韋布爾分布和正態分布更為接近，但不能說明具體與哪一分布相匹配，還需要通過假設檢驗進一步驗證。

圖3 第100幀數據擬合結果

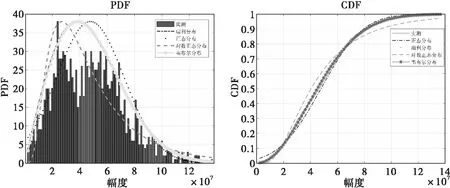
圖4 第280幀數據擬合結果

兩組數據的時間相關性和空間相關性結果如圖5和圖6所示。可以看出，大下視角下的地雜波具有秒級的時間相關性，每個雷達相參處理周期內每個距離是相關的；但大下視角下的地雜波的空間相關性很低，相鄰距離單元之間相互獨立，不存在相關性。

圖5 第100幀數據相關性

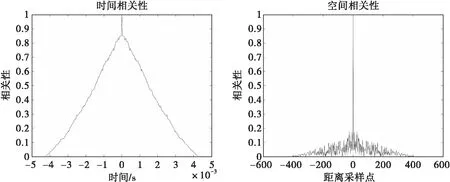
圖6 第280幀數據相關性

采用卡方檢驗對PDF和CDF擬合結果進行進一步驗證，結果如表3示。對這兩幀數據采用5%顯著水平進行檢驗，結果表明大下視角下的地雜波服從韋布爾分布，可見，雖然雜波背景都是戈壁區域，但由于雷達運動姿態的改變，在大下視角下，地雜波不再服從瑞利分布，雜波散射點不再保持同一水平，強散射點所占的比例增加，雜波分布由均勻變得不均勻，而傳統的單元平均恒虛警檢測器無法將這些強散射點抑制，這些都影響了雷達的目標檢測性能。

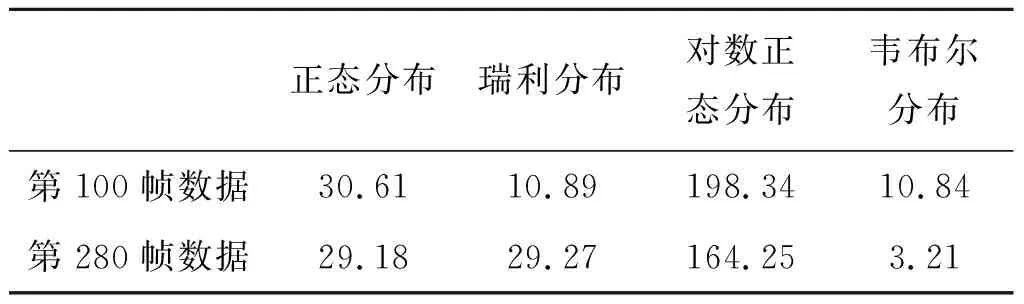
表2 5%顯著水平卡方檢驗結果

3 結束語

通過對大下視角下地雜波的實測數據進行分析，可以看出由于雷達運動姿態和照射區域地形的變化，地雜波回波中的強散射點出現的概率增大，整體上由均勻變得非均勻，逐漸偏離瑞利分布，服從韋布爾分布，導致傳統的單元平均恒虛警檢測器不再適用，應采用非均勻環境下的檢測器，如排序類檢測器、單元選大恒虛警檢測器、智能檢測器等。

這樣，為非均勻雜波環境中的目標檢測和雜波抑制算法提供了理論依據。在后續的雜波抑制算法設計中，可以重點研究非均勻雜波環境下的目標檢測算法，為提高大下視角下雷達的檢測性能提供理論支撐。