橋基荷載對岸坡穩定性影響的研究

王 鵬，杜國超，王理想，謝 寧，董海龍

(1.浙江交工集團股份有限公司西南分公司，貴州 貴陽 550001；2.貴州理工學院，貴州 貴陽 550001)

0 前 言

云貴高原地區地形地貌復雜，山谷縱橫，地表起伏不平，區域內因公路、鐵路等交通路線建設形成的橋梁、隧道較多。因橋梁建設而形成的兩岸邊坡巖體結構復雜，在自然應力及橋梁建設、運營期的工程擾動等外界因素的影響下，容易形成岸坡失穩破壞隱患，威脅岸坡的穩定，進而對橋梁的施工及運營安全產生巨大隱患。鑒于此，對橋位邊坡的穩定性進行科學合理的分析，進而為岸坡的支護方案的參數選取以及補強方案的設計提供參考，具有極為重要的研究及工程價值。

近年來，在我國西南山區道路工程快速建設發展的背景下，中外學者專家對于橋梁岸坡穩定性分析方面的研究取得了一定的成果。橋位邊坡因受橋基荷載的影響，其穩定性分析相對更加復雜。費力等[1]基于勘察資料結合現場調查，分析岸坡坡體結構特征，并由此確定擬建橋基岸坡的破壞模式、潛在失穩區域及主滑方向，運用赤平投影法評價該橋基岸坡的穩定狀態。蔡家鵬等[2]采用結構面空間幾何分析法及岸坡巖體應力應變的數值模擬相結合的方法，研究了水盤城際鐵路北盤江特大橋岸坡巖體的變形破壞趨勢及可能的失穩特征，對岸坡巖體的穩定性進行了定性和定量的評價。武博強等[3]針對風積沙地區公路橋梁岸坡設計中施工便道岸坡模型構建的困難性，提出一套基于實際施工環境下的岸坡穩定性分析方法，利用極限平衡法確定了最危險滑面位置。高國紅等[4]利用潘氏原理確定出抗滑剪應力的方向，對某順層橋址岸坡的穩定性進行對比分析，驗證了三維矢量和方法在岸坡穩定性評價的適用性。He Lei等[5]采用FLAC3D有限差分軟件建立橋基荷載對巖質邊坡穩定性影響分析模型。王鵬[6]綜合半球赤平投影法、極限平衡sarma法、數值模擬法、離散元模擬法等多種手段，對金沙江特大橋岸坡穩定性進行了綜合評價。

鑒于橋基荷載是影響岸坡穩定的主因之一，本文以貴州仁遵高速公路工程某特大橋梁岸坡為工程背景，采用ABAQUS有限元軟件多模型對比的方法就橋基荷載對岸坡穩定性的影響展開研究，深入剖析其對岸坡應力、位移及塑性區分布的影響規律，綜合分析岸坡的穩定性，為橋梁岸坡穩定性分析相關的理論研究與工程實踐運用提供參考。

1 工程概況

本文以貴州仁遵高速某在建公路橋梁遵義岸岸坡為研究對象，該工程位于云貴高原東北部，遵義市的北西面。由于受到溶蝕-剝蝕作用等影響，屬中等切割的侵蝕～溶蝕中山地貌和溶蝕槽谷及溶蝕峰叢相間地貌。橋下河谷寬約40～70 m，是典型的“V”形谷。遵義岸岸坡體整體較陡，自然坡度角在40°～50°，橋區大部分基巖裸露，植被發育，整個坡體軸線地面高程在953.4～649.6 m，相對高差303.8 m。通過地表調查，結合鉆孔電視、鉆探巖芯、槽探結果，岸坡巖體巖性較差，由二疊系地層組成，二疊系下統龍潭組二疊系上統龍潭組粉砂質泥巖、泥巖夾煤層。該段地質構造簡單，巖層單斜構造，無斷層構造。該岸坡施工實況圖如圖1所示。

圖1 邊坡實況圖

遵義岸岸坡為二級巖質切向邊坡，全長135 m，邊坡最大高度為22.53 m，采用1∶0.25～1∶1.5坡率放坡。遵義岸拱座基坑邊坡采用局部清方、抗滑樁和錨索支擋。第一級邊坡采取錨拉樁，樁截面尺寸2 m×3 m，樁長32 m，錨索沿樁身從上往下布置2排，抗滑樁樁頂設置冠梁，抗滑樁樁頂以上坡體沿層面進行順層清方減載。減載后邊坡坡面采用豎梁錨索和框架錨索加固，錨索排數為4排；在左24#墩、右23#墩處坡面采用豎梁錨索和框架錨索加固，錨索排數為3排；預應力錨索采用7φ15.24高強度低松弛鋼絞線，鋼絞線標準強度不小于1 860 MPa，每孔設計噸位900 kN。左幅24#墩、右幅23#采用高承臺設計。坡口線外設置截水溝，平臺設置平臺截水溝加強排水。

2 復合材料參數確定

為分析橋基荷載對遵義岸岸坡穩定性的影響，根據目前有關研究現狀，以采用有限元法為宜。如圖2所示，根據該岸坡橫截面及有關施工、設計文件資料，采用ABAQUS軟件建模得到平面二維數值模擬計算模型。

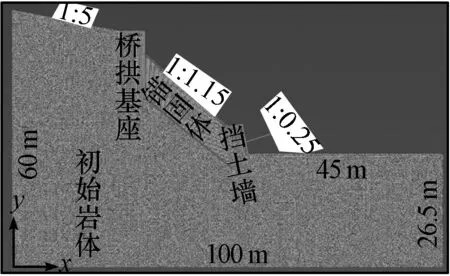
圖2 數值模型概況及其網格劃分

分析圖2可知，該橋位邊橋為二級邊坡，坡率分別為1∶1.15和1∶5，橋拱基座位于二級坡面坡趾處。一級坡面采用豎梁錨索和框架錨索加固，坡底構筑擋土墻，擋土墻坡率為1∶0.25。其中，初始巖體視為均質連續原巖體，橋拱基座、擋土墻為鋼筋混凝土復合材料，錨固體為由原巖和鋼混結構組成的復合材料。就目前的數值模擬研究而言，通常采用桁架(truss)、梁(beam)等桿件單元來模擬復合材料中的鋼筋，能夠反映鋼筋剛度貢獻對混凝土的預壓作用。但采用常規的位移協調模式進行有限元數值計算時，要求鋼筋單元節點必須與混凝土單元的節點重合，這在實際操作中因鋼筋的幾何及方位參數受有限單元網格的約束等原因難以實現，致使目前鋼混結構的有限元仿真模擬不易實現且計算結果的精度難以保證。

為此，本文引入基于均勻化思想的鋼筋密度因子k，均勻化思想等效材料的強度參數受混凝土(或巖體)參數和鋼筋參數的共同影響，鋼筋參數主要包括圖3中的鋼筋的半徑r(m)及其豎向間距Lv(m)和水平排距Lh(m)，這些參數共同影響著等效復合材料的強度。

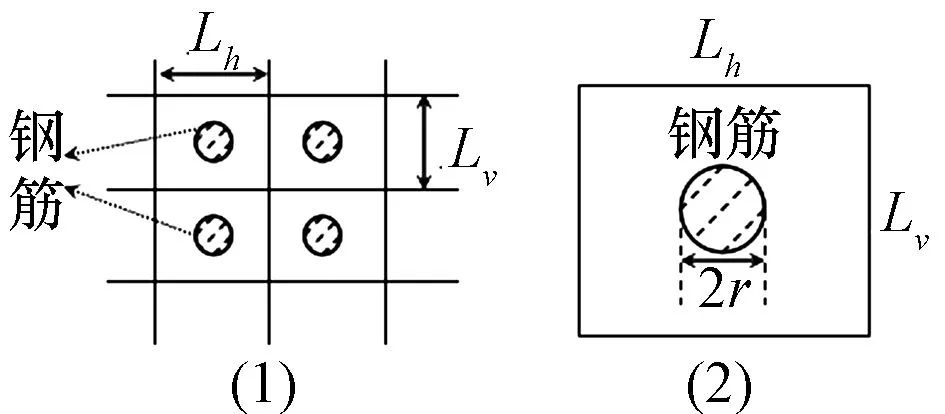
圖3 鋼筋混凝土復合材料作用模式

參考Indraratna等[7]提出的方法，引入能夠反映鋼筋摩阻力的鋼筋密度因子描述等效復合材料的強度，鋼筋密度因子可表示為：

k′=2πrτ/LvLh

(1)

式中，k′為無量綱標量化的鋼筋密度因子；τ為鋼筋與混凝土(或巖體)之間的摩阻系數，其大小與鋼筋表面的光滑程度負相關，使用螺紋鋼筋時取τ=tanφ(φ為混凝土或巖體材料的內摩擦角，(°))，若使用無螺紋鋼筋時，取τ=tan(φ/2)。

通過簡單驗算可以發現，在多數文獻中[7-8]的鋼筋密度因子k被錯誤地定義為量綱為m-1的參量，這顯然是不可取的。鑒于此，筆者通過引入單位長度L(即1 m)的方式修正這一錯誤。修正后的鋼筋密度因子可表示為：

k=(2πrτ/LvLh)·L

(2)

顯然，修正后的鋼筋密度因子k已無量綱化，是正確可取的。

對于均勻化處理后的等效復合材料，仍然滿足Mohr-Coulomb強度準則，只是加筋后材料屈服軌跡上移導致梯度(F)上移和截距(H)增加，這種變化可表示為：

(3)

式中，c*、φ*分別為復合材料的等效黏聚力，MPa和等效內摩擦力，(°)；c、φ分別為素混凝土的黏聚力，MPa和內摩擦力，(°)。

對上式進行簡單幾何計算即可得到等效復合材料的等效黏聚力和等效內摩擦角為[8]：

(4)

根據均勻化方法，等效復合材料的彈性模量和密度可參照鋼筋和原材料所占截面經加權平均后求得。據此可得，復合材料的等效彈性模量為：

E*=[Ebπr2+E(LlLr-πr2)]/LlLr

(5)

式中，E*、Eb、E分別為復合材料、鋼筋及素混凝土(或原巖)彈性模量，GPa。

復合材料的等效密度可類似求得：

ρ*=[ρbπr2+ρ(LlLr-πr2)]/LlLr

(6)

式中，ρ*、ρb、ρ分別為復合材料、鋼筋及素混凝土(或原巖)密度，kg/m3。

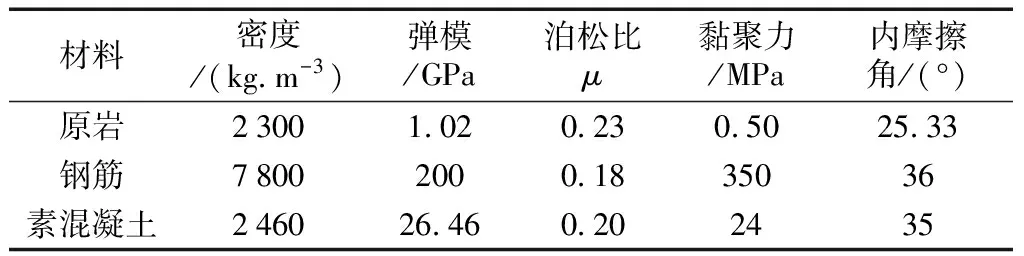
表1 均質材料屬性

表1所列為數值模擬輸入的原巖、鋼筋及素混凝土等均質材料的主要參數。根據前述等效計算方法，可以得到圖2模型中的復合材料(即：橋拱基座、擋土墻以及錨固體)的材料參數，結果如表2所示。表2所列即為本文數值模擬所需輸入的復合材料參數。

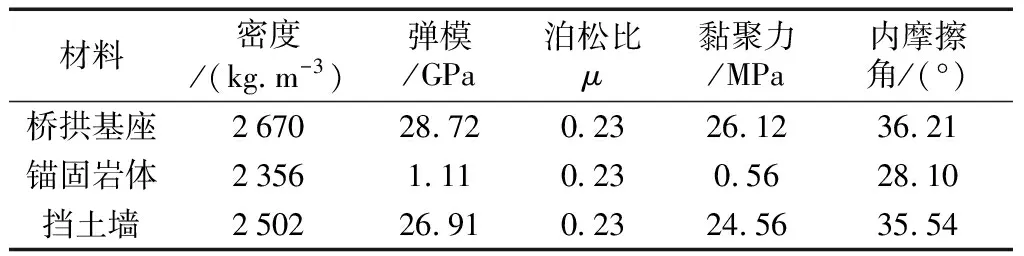
表2 等效換算的復合材料屬性

3 建模計算

1)建模概況。利用大型有限元分析計算軟件ABAQUS，根據前述橋位岸坡工程實況，建立平面岸坡模型用以對比分析不同橋基荷載條件下的邊坡應力應變及位移分布等情況，模型尺寸如圖2所示。

2)材料定義。模擬時岸坡均質及等效復合材料的破壞均遵循Mohr-Coulomb準則，材料定義時將表1和表2所列參數按圖2材料模塊輸入軟件即可。

3)邊界條件與載荷。模型左右邊界水平位移設置為0，底邊界水平、豎向位移設置為0；模型整體施加重力荷載，重力加速度取9.81 N/kg；橋拱基座上表面施加均布荷載用以模擬橋體作用于橋基的應力，均布荷載大小用ABAQUS場變量設置的方法，以1 MPa為步長，由1 MPa逐步增長至11 MPa。

4)劃分網格。為確保計算精度，采用6節點修正二次型三角形平面應變縮減積分單元將邊坡模型劃分為32 991個單元。

完成上述步驟，建立分析步后提交計算即可。

4 計算結果對比分析

1)應力對比分析。如圖4所示，為橋拱基座均布荷載F分別為1、4、7、11 MPa時的有限元模型Mises應力分布情況。

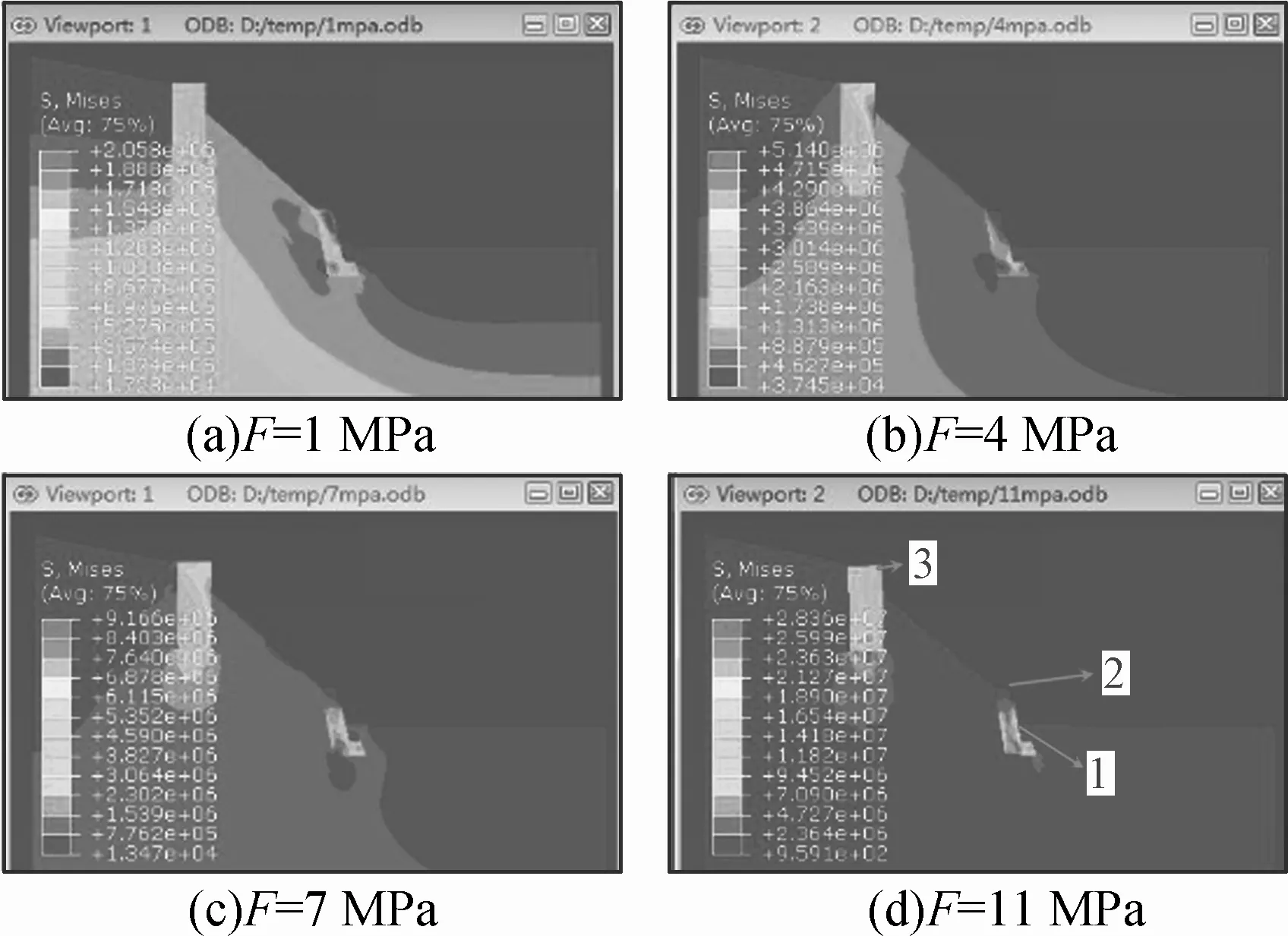
圖4 模型應力分布隨橋基荷載的變化

由圖4可明顯看出，隨著F不斷增大，不僅坡體應力整體大小在不斷增加，橋拱基座及擋土墻周邊的應力集中程度也越來越高，由此可見，F對岸坡巖體的應力分布影響較大，對橋基及擋土墻的強度要求較高。

2)位移大小分析。圖5所示為邊坡坡趾、擋土墻頂點及橋拱基座頂點處(如圖4所示的1、2、3質點)的水平位移U1隨橋拱基座荷載F的變化曲線。

由圖5可知：①質點1水平位移最大、質點2次之，質點3最小；②3個質點的水平位移隨F的變化趨勢基本一致，即F≤8 MPa時，位移很小且幾乎沒有明顯變化；當F=8 MPa時，位移開始發生突變；F>8 MPa后，水平位移隨F快速增大致使邊坡失穩；③若根據位移突變性判據，橋基荷載F應小于8 MPa，否則岸坡將失穩破壞。

圖5 U1隨F的變化曲線

3)塑性區分布對比分析。如圖6所示，為岸坡巖體塑性區分布隨橋拱基座荷載F的變化情況。

圖6 岸坡坡塑性區分布隨F的變化

分析圖6可以得到，岸坡塑性變形由橋拱基座底部開始發展并逐步向外擴張；當F=5 MPa時，擋土墻內側塑性區開始形成并隨F的增大逐步擴展；當F=8 MPa時，塑性區剛好貫通，岸坡開始失穩破壞。因此，根據塑性區貫通判據，橋基荷載F應小于8 MPa，否則岸坡將失穩破壞。

4)邊坡穩定性分析。邊坡穩定性有限元分析時，常以有限元模型計算不收斂作為邊坡安全的判據，若如此，經計算可知，F=11 MPa時，模型剛好不收斂。即：確保岸坡穩定的臨界F值為11 MPa。這相比于上述基于突變性判據和塑性區貫通判據得到的橋基荷載F都應小于8 MPa的結論更不利于邊坡的穩定。

綜上，就利于邊坡穩定而言，研究時宜以位移突變性判據或塑性區貫通判據為基準，即橋基荷載F應小于8 MPa。

5 結 論

采用均勻化思想等效計算復合材料等效強度參數，以ABAQUS為工具對橋基荷載為0～11 MPa時遵義岸岸坡的穩定性進行數值模擬計算，得出以下結論。

1)從均勻化思想出發，通過引入鋼筋密度因子的方法計算了錨固復合巖體的強度參數，為錨固巖體的數值模擬計算提供便利。

2)隨著橋基荷載F的不斷增大，坡體應力分布集中程度、位移大小及塑性區分布范圍均逐漸增大。以模型計算不收斂為判據，F為11 MPa，基于突變性判據和塑性區貫通判據得到的橋基荷載F均為8 MPa。

3)就利于岸坡穩定而言，分析計算時宜以位移突變性判據或塑性區貫通判據為基準，即橋基荷載F應小于8 MPa，以確保岸坡的穩定。

4)橋基荷載對橋位邊坡的穩定性具有顯著影響，荷載越高，穩定性越差。為此，公路橋梁施工過程中，應密切關注橋基荷載的增加對岸坡穩定性的影響。

[ID：013810]