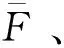基于Laguerre-Voronoi法的三維開孔泡沫金屬模型
吳允兵, 陳曄, 聶政威
(南京工業大學機械與動力工程學院, 南京 211816)
泡沫金屬是指含有泡沫氣孔的特種金屬材料,它是一種具有超低密度、高比表面積、高比強度,一般孔隙率在40%~97%的具有多孔特性的泡沫狀金屬新型材料[1-2]。開孔泡沫金屬由于其相互連通的網狀結構有著非常大的比表面積,導熱性能好,流動阻力相對較低,結構的擾動作用也大大提高了換熱效果[3-5]。開孔泡沫金屬是強化對流換熱的優良載體[6-7],在能源、化工及電子等領域具有廣闊的應用前景,故其研究對工程應用具有重要價值。
該研究領域的許多學者提出了建立開孔泡沫金屬模型的不同方法,從總體來看主要歸納為三種建模方法。第一種建模方法是利用泡沫的數字化影像或斷層影像去重新構建真實的泡沫結構,其中使用較多的方式有X射線斷層掃描和磁共振成像,它們以一種非破壞性和非侵入性的方式獲得泡沫內部結構[8-9]。第二種方法是采用開爾文泡沫空間模型,開爾文晶胞結構也稱之為十四面體,由十四個面(八個六邊形面和六個四邊形面)和二十四個頂點組成[10-11]。這種方法構建的是理想的周期性泡沫結構,且開爾文模型表現出一些特殊的力學性能,其還未從真實材料中得到證實。當前已經有一些研究人員聲稱開爾文模型不能真實呈現泡沫內部結構,因為其缺乏隨機性而不能真正表現泡沫的某些力學性能[10]。
為了得到隨機無規律的泡沫結構,許多研究者采用不同的方法來達到真實泡沫的隨機性,第三種泡沫金屬結構建模的方法隨之出現。目前大多數研究者通過Voronoi空間劃分法、Laguerre-Voronoi空間劃分法和Poisson-Voronoi空間劃分法生成泡沫隨機結構模型[12-13]。在這種建模方法中,需要在空間中隨機設定某些點,通過定義該點最鄰近的空間生成泡沫單孔,這種泡沫結構的隨機性受到設定點空間分布的強烈影響。然而,通過Voronoi空間劃分法產生的泡沫結構每個頂點的支柱數量高于真實泡沫結構的支柱數量,通過Poisson-Voronoi空間劃分法產生的泡沫結構參數也與實際泡沫不同[14-15]。Wejrzanowski等[15]提出了使用Laguerre-Voronoi空間劃分法建立開孔泡沫金屬模型,將所建模型的孔隙率和表面積與實驗數據進行對比并修正,結果表明該模型比另外兩種模型更加貼合實際泡沫內部結構。
為了很好地呈現開孔泡沫金屬內部結構,現基于Laguerre-Voronoi法對封閉空間內隨機堆積的球體進行空間劃分來建立開孔泡沫金屬三維模型,分析變異系數對泡沫孔隙分布的影響,并與商用開孔泡沫金屬進行對比驗證。
1 模型的建立與方法
1.1 Laguerre-Voronoi空間劃分法
Laguerre-Voronoi空間劃分法是一種基于加權的Voronoi空間劃分方法[13]。對于集合S中的任意一點pi,加權數ri組成一個集合r={r1,r2,…,rn},則集合S中任意點pi和其他任意點q之間的距離表達式為
dL(pi,q)={[dV(pi,q)]2-ri2}1/2
(1)
式(1)中:dL表示Laguerre幾何中兩點間的距離;dV表示兩點間的歐氏距離。
則點pi所對應的單個劃分空間表達式為
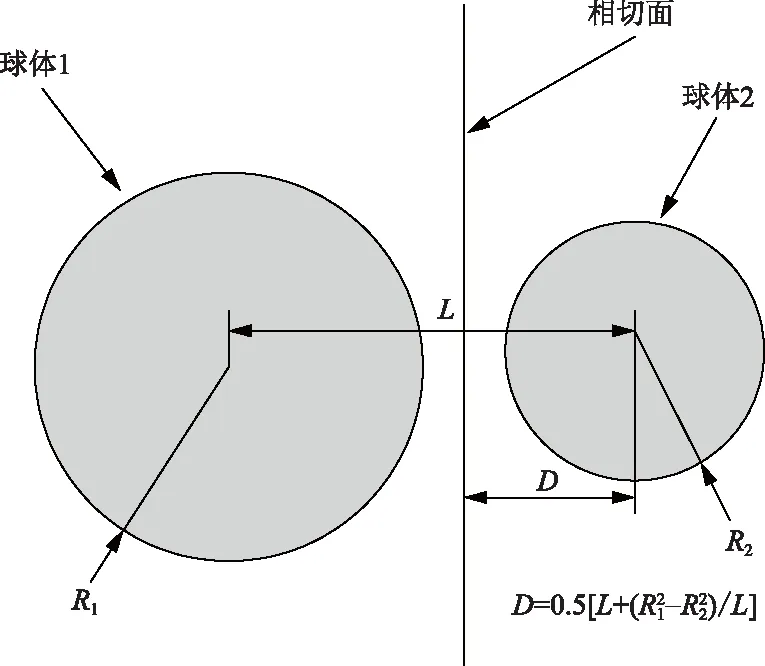
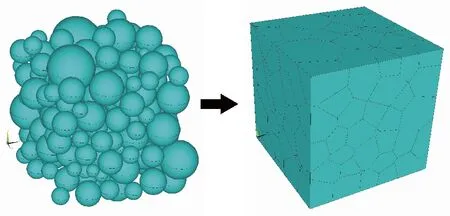
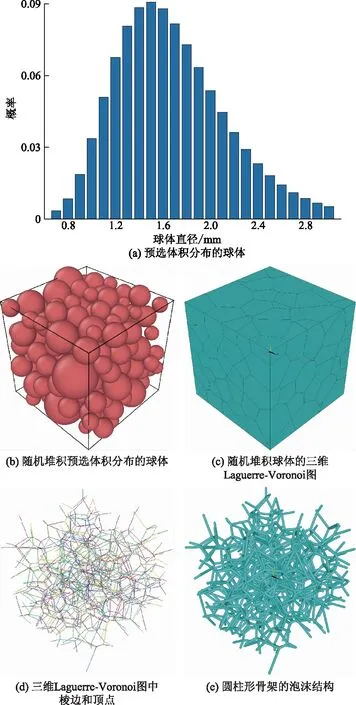
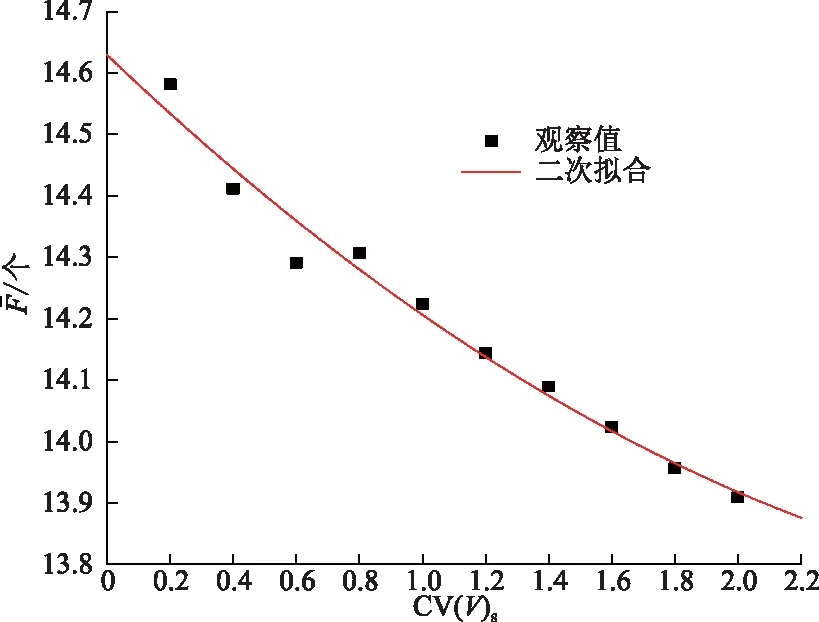
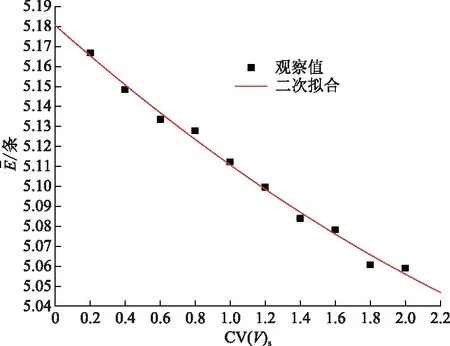
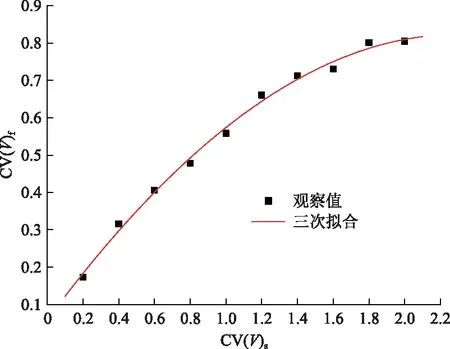
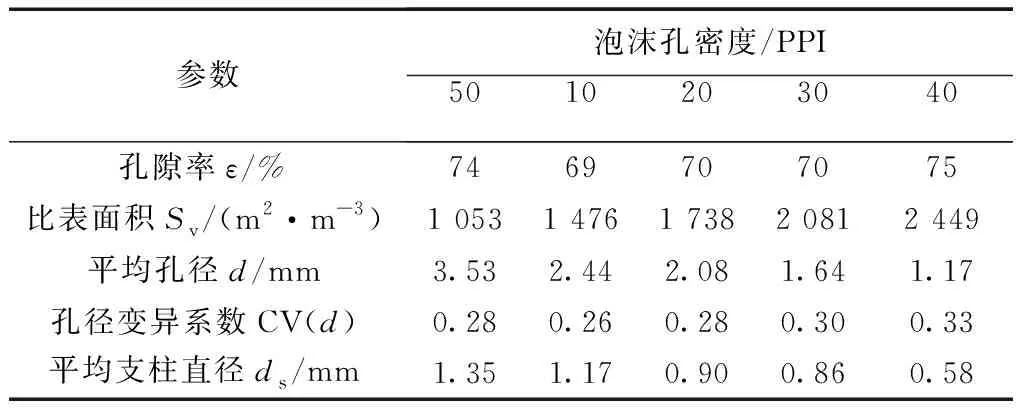
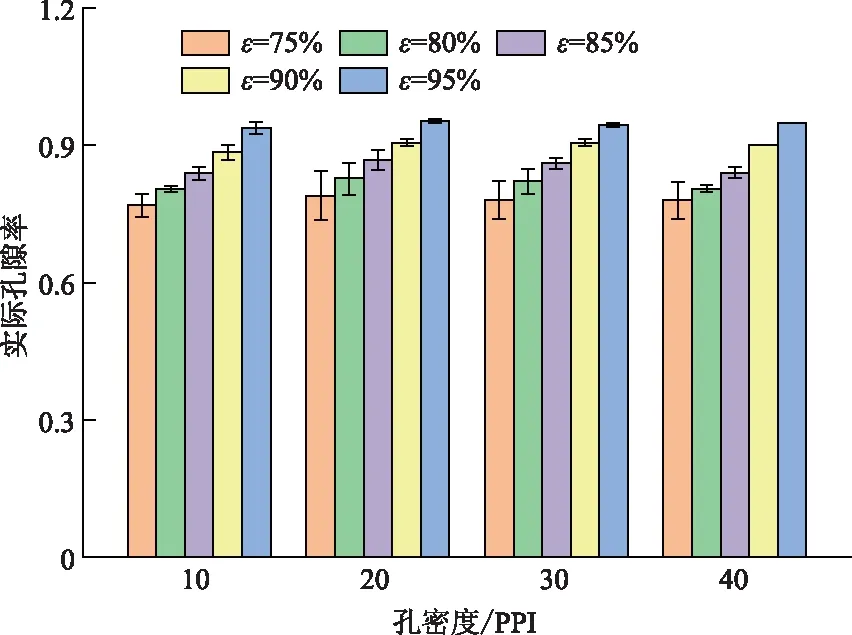
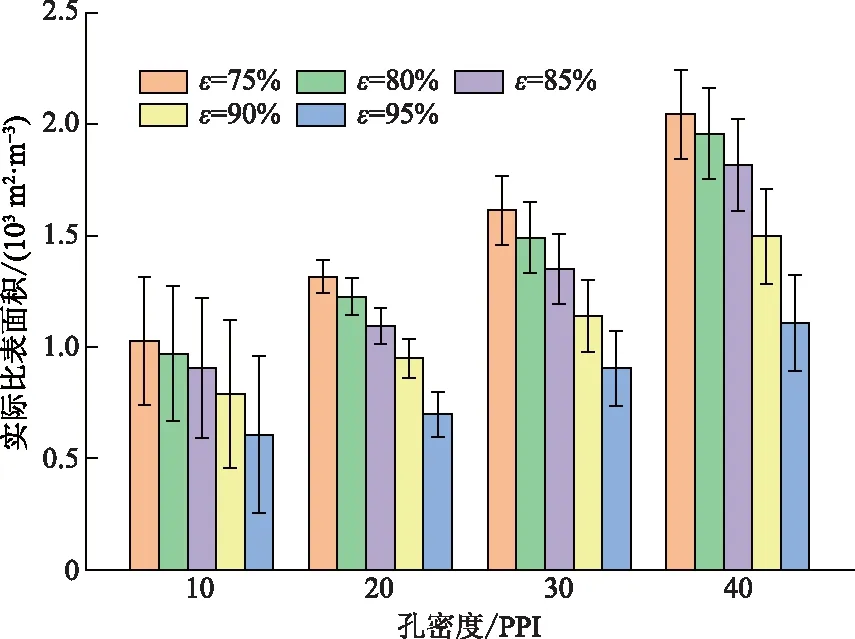
vL(pi)={p|p∈R3,dL(p,pi) (2) 則所有劃分空間的表達式為 VL(S,r)={vL(p1),vL(p2),…,vL(pn)} (3) 因此,在空間劃分后所呈現的圖形被稱為Laguerre-Voronoi圖,如圖1所示。 圖1 二維Laguerre-Voronoi圖Fig.1 2D Laguerre-Voronoi diagram 提供所有堆積球體中心坐標所組成的集合S以及相應球體半徑的集合r,采用Laguerre-Voronoi空間劃分法劃分固定空間內隨機堆積的球體得到Laguerre-Voronoi圖,其空間劃分方法如圖2所示。 在Laguerre-Voronoi圖中,每個球體都被相對應的劃分空間單獨包圍著,相鄰的劃分空間則包圍著相鄰的球體,兩個相切球面的相切平面就是相應多面體的共享面。因此,劃分的空間體積分布受到初始球體體積分布的強烈影響。為了提高計算效率,采用APDL語言編寫的程序腳本運行,其中隨機堆積球體的三維Laguerre-Voronoi圖如圖3所示。 圖2 Laguerre-Voronoi法空間劃分規則Fig.2 Space division rules of Laguerre-Voronoi method 由于實際泡沫制造工藝中存在隨機性和不完整性,泡沫的孔隙體積變異系數一般在1.09~2.03,實際泡沫孔隙體積分布呈現對數正態分布[16]。因此,需要控制固定空間內隨機堆積的球體分布具有一定的對數正態分布。 圖3 基于隨機堆積球體的三維Laguerre-Voronoi圖Fig.3 3D Laguerre-Voronoi diagram based on randomly stacked spheres 本文所進行的開孔泡沫結構建模主要包括以下五個步驟。 (1)利用MATLAB軟件編寫程序生成具有規定尺寸分布的球體,在程序中設置預先設定的球體體積變異系數CV(V)和平均體積E(V)。 (2)利用LAMMPS軟件運行固定立方體空間內隨機堆積該組球體的程序腳本。 (3)在APDL中通過運行程序腳本,利用Laguerre-Voronoi空間劃分法劃分該組隨機堆積球體模型,獲得相應的三維Laguerre-Voronoi圖。 (4)刪除步驟(3)中三維Laguerre-Voronoi圖的堆積球體、每個球體對應的劃分空間內部體積和各空間之間的界面,僅保留各球體劃分空間的棱邊和頂點。 (5)將步驟(4)生成的模型文件導入ANSYS中,將保留的邊緣進行圓柱化以生成金屬骨架材料;為減少邊界效應并提高計算效率,在SolidWorks軟件中進行模型切割,獲得開孔泡沫金屬三維模型。 基于以上五個步驟給出開孔泡沫建模步驟示意圖如圖4所示。 對數正態分布是許多工程材料結構的特征代表。因此,研究采用對數正態分布來分析泡沫結構的系列數據。對數正態分布的概率密度函數表達式為 (4) 式(4)中:μ和σ分別為變量對數的平均值和標準差,期望值E(x)和方差Var(x)由μ和σ兩個參數構成,表達式為 E(x)=e[μ+(σ2/2)] (5) Var(x)=(eσ2-1)e2μ+σ2 (6) 變異系數CV(x)由標準差SD(x)和期望值E(x)構成表表達式為 圖4 開孔泡沫金屬三維建模流程示意圖Fig.4 Schematic diagram of 3D modeling process for open cell metal foams (7) 式(7)中:SD(x)=Var(x)1/2。 圖5~圖7分別呈現的是基于孔密度為20 PPI(pores per linearinch)、球體體積變異系數CV(V)=0.4的對數正態分布下隨機堆積球體所形成的泡沫孔隙體積、面數和邊數分布直方圖以及采用相應參數擬合對數正態分布。 圖5 泡沫孔隙體積直方圖和相應參數擬合的對數正態分布Fig.5 Histogram of foam pore volumes and lognormal distribution of corresponding parameter fitting 圖6 每個泡沫孔隙(多面體)面數直方圖和 相應參數擬合的對數正態分布Fig.6 Histogram of face number per foam pore(polyhedron) and lognormal distribution of corresponding parameter fitting 圖7 泡沫孔隙每個面的邊數直方圖和 相應參數擬合的對數正態分布Fig.7 Histogram of edge number of per surface of foam pore and lognormal distribution of corresponding parameter fitting 14.629 8,σ= 0.032 5 (8) 5.180 6,σ= 0.003 2 (9) 標準殘差對于CV(V)f和CV(V)s之間的關系采用三次擬合,得到表達式為 CV(V)f=-0.003 4[CV(V)s]3-0.129 5× [CV(V)s]2+0.648 0CV(V)s+ 0.058 8,σ= 0.014 8 (10) 式中:σ為標準殘差。從圖8~圖10可以看出,當隨機堆積球體的球體體積變異系數以0.2為間隔從0.2遞增到2.0時,泡沫結構中每個孔隙的平均面數從14.58遞減到13.91,泡沫結構中每個面的平均邊數從5.17遞減到5.06,但泡沫結構中孔隙體積變異系數從0.17遞增到0.80。圖10也驗證了可以通過改變隨機堆積球體的球體尺寸參數來控制泡沫結構中孔隙尺寸的變化。 本文模型的驗證是基于Wejrzanowski等[15]所做的工作,其中提出泡沫結構的支柱形狀是一個重要的幾何特征。大多數已有研究都將Laguerre-Voronoi圖中劃分空間的邊緣簡化成直徑不變的圓柱體,在一些前者的研究中模型支柱的頂點重疊被忽略不計,未進行相關的誤差評估。為了更好地分析泡沫結構,用泡沫孔隙直徑d代替泡沫孔隙體積V,兩者的關系表達式為 (11) 圖8 泡沫結構中每個孔隙的平均面數與相應 隨機堆積球體的球體體積變異系數的關系Fig.8 The relationship between average number of faces per pore in foam structure and sphere volume variation coefficient of corresponding randomly stacked sphere 圖9 泡沫結構中每個面的平均邊數與相應 隨機堆積球體的球體體積變異系數的關系Fig.9 The relationship between average number of edges per face in foam structure and sphere volume variation coefficient of corresponding randomly stacked sphere 圖10 泡沫結構中孔隙體積變異系數與相應 隨機堆積球體的球體體積變異系數的關系Fig.10 The relationship between variation coefficient of pore volume in foam structure and sphere volume variation coefficient of corresponding randomly stacked sphere Wejrzanowski等[15]提出了一種頂點重疊的校正方法,引用其校正的泡沫孔隙率和比表面積表達式為 (12) Sv=[7.38e-1.35CV(d)E(d)-2πds]- (13) 式中:CV(d)為孔徑的變異系數;E(d)為平均孔徑,mm;ds為泡沫骨架支柱直徑,mm。 采用不同孔密度的商業氧化鋁泡沫對這里提出的模型進行驗證,文獻[15]中對典型樣本進行三維X射線斷層掃描來評估泡沫結構特性,然后采用圖像分析法對結構參數進行測量,結果如表1所示。 參考表1中平均孔徑E(d)和孔徑變異系數CV(d)來控制球體體積對數正態分布進而改變泡沫的孔密度,采用式(12)對泡沫孔隙率進行改變,得到不同孔密度(10、20、30、40 PPI)和不同孔隙率(75%、80%、85%、90%、95%)的三維開孔泡沫金屬結構。在不同孔密度以及不同孔隙率條件下,對理論孔隙率與實際孔隙率進行誤差分析(圖11),總體來看,相對誤差均小于±5%。同時作理論比表面積和實際比表面積誤差分析(圖12)圖,對于孔密度為10 PPI且不同孔隙率下的開孔泡沫金屬模型,相對誤差較大(28%~35%),這是由于在SolidWorks軟件中模型的切割具有隨機性所造成的,但是其余泡沫金屬模型相對誤差均小于20%。 圖13(a)是本文所建立的孔密度為20 PPI泡沫三維模型,泡沫骨架結構是直徑不變的圓柱體,截面形狀為圓形;圖13(b)是基于本文所建立的模型進行3D打印的開孔泡沫,使用的材料是鑄造鋁合金AlSi10Mg;圖13(c)是從市面上購買的由電沉積法制造的孔密度為20 PPI的泡沫銅,從圖13中可以看出泡沫骨架截面形狀為凹三角形。因此,本文建立的三維開孔泡沫金屬模型存在一定的誤差,但是可以很好地呈現實際泡沫的內部結構。 表1 三維X射線斷層掃描的泡沫結構Table 1 Foam structure of 3D X ray tomography 圖11 實際孔隙率誤差分析Fig.11 Error analysis of actual porosities 圖12 實際比表面積誤差分析Fig.12 Error analysis of actual specific surface areas 圖13 泡沫結構誤差分析Fig.13 Error analysis of foam structure (2)通過與理論結構參數對比分析,整體來看泡沫孔隙率的相對誤差小于±5%,比表面積的相對誤差普遍小于20%;對商用開孔泡沫金屬進行電鏡掃描分析,顯示本文所建立的模型存在一定的誤差,但是該開孔泡沫金屬建模方法可以很好地呈現實際泡沫內部結構,可以為泡沫結構的研究提供一定的參考。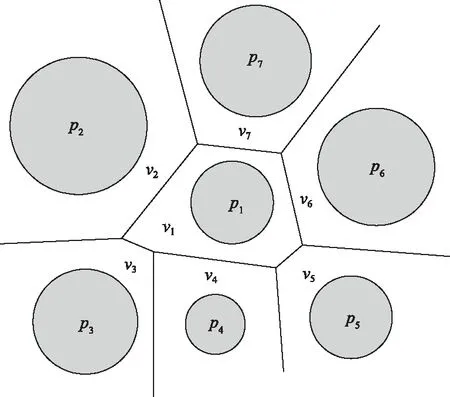
1.2 基于隨機堆積球體的Laguerre-Voronoi空間劃分法
1.3 建模過程
2 結果與討論
2.1 泡沫孔隙的體積、面和邊數分布
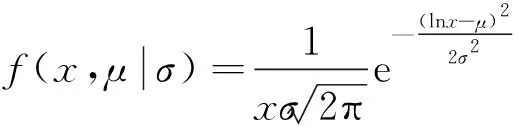
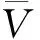
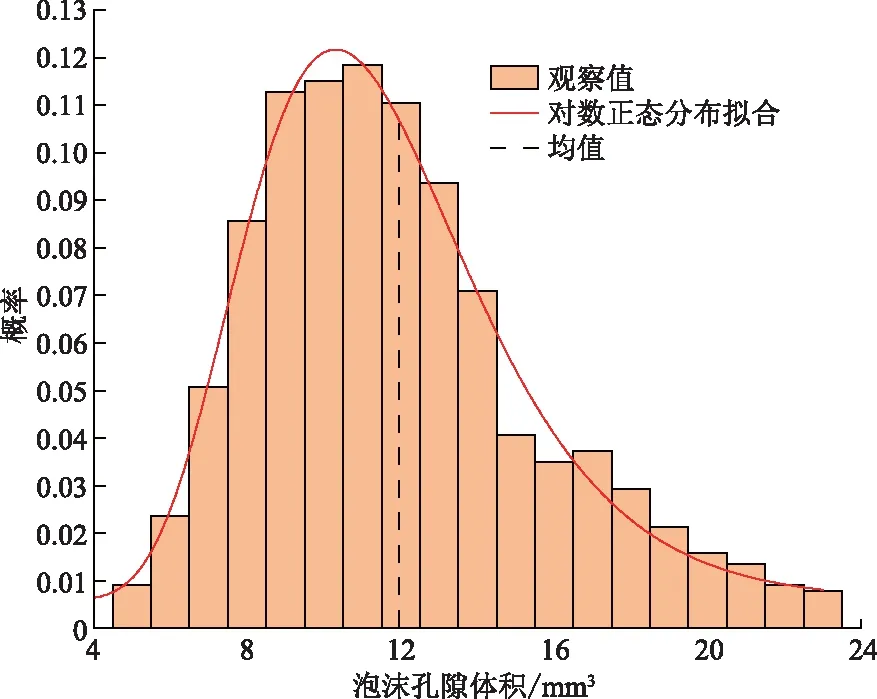
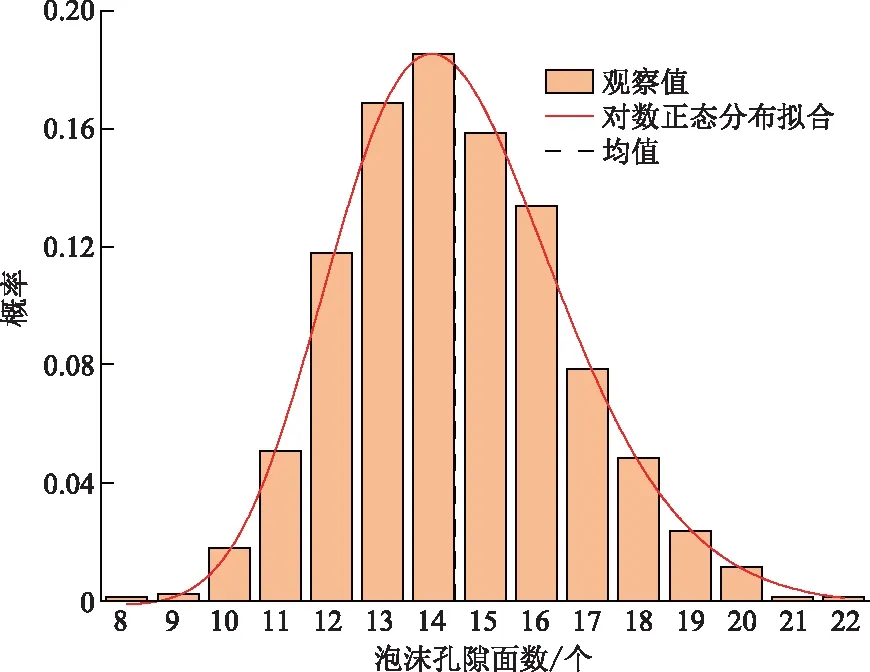
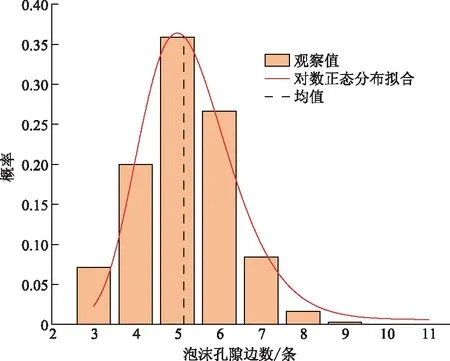
2.2 泡沫孔隙不均勻性影響
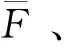
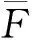
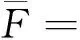
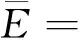
2.3 分析驗證
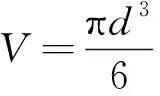
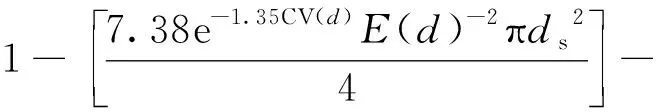

3 結論