多維度動態融合建模下4D飛行路徑優化

李夏， 張飛橋 ， 嚴皓 ， 馬昕

(中國民用航空飛行學院空中交通管理學院, 廣漢 618307)

隨著計算機各類功能的強化和元學習算法的推廣，民用客機的運行控制對航跡預測日漸重視[1]，愈發依靠運行參數、空域數據和時間進程，對空域內的航空器數量、空間位置和空中交通管制態勢進行分析和評價，由此設計4D飛機路徑，推導出目標時間段內的運行情況前瞻結論，實現提升飛行安全和運行效率的目的[2]。4D飛行路徑研究的核心內容是運行數據的采集提煉、綜合分析和計算評價，且數據精細化程度要求較高[3]，其數字化體現在各類運行參數的預先處理和特征分析[4]，智能化體現在航空數據評價結論的科學使用[5]，對航班進、出港預計時間，飛機飛行各階段空間相對位置關系[6]，即將可能面臨的外部干擾與預期燃油消耗量[7]，飛行各階段航空器性能與運行環境的適應性等，這些都是飛行任務能否按計劃實施的重要影響因素，也是飛行路徑規劃與管理的基本參數[8]。

4D飛行路徑規劃現階段研究主要集中在以下幾個領域。首先是混合空域內聯合運行研究，因智能物流技術的興起和發展，以大型固定翼無人機為載體的航空物流逐步由實驗轉變為試運行，受機場數量、民用空域范圍等諸多條件不足的限制，民航客機和大型無人機的運行矛盾較為突出[9]。在此背景下，張軍峰等[10]對4D飛行路徑規劃的基本模型、算法進行了概念描述和歸類；呂開妮等[11]開展了水平航跡的預測，提出了動態時間規整方法；劉杰等[12]在此基礎上，搭建了無人機速度剖面模型，對進場時間管理提供了參考。但該方向的研究主要集中在無人機性能的模型建立，對民航客機的分析和評價缺少支撐[13]。其次為空域規劃方法的創新，王寧等[14]提出了基于點融合規劃4D飛行路徑規劃的方法，大幅提升終端區航班運行效率，但由于可適用點融合技術設計的機場和空域需具有流量較大、管制扇區較豐富的特點，且該技術僅可在進場飛行階段提供計算，缺少了飛行各階段評價的全面性。第三類是沖突評價模型的研究，丁松濱等[15]通過建立航空器沖突預警指示函數，可實現短時間內的4D飛行路徑預測結論可靠性分析，但該類研究的時間維度考慮欠全面，預測時間推進較短，不適用于儀表飛行全過程。綜上所述，現階段研究成果為4D飛行路徑預測建立了理論基礎，具有一定借鑒意義，為順應民航智慧空管發展趨勢，建立飛行全過程評價策略，實現航空信息精準利用，面向多維度考慮下的4D飛行路徑優化研究還存在可深入研究的空間。

1 問題描述

4D飛行路徑規劃是基于航空器傳統三維航跡，即經度、緯度和高度的基礎上，融入時間維度開展飛行路徑規劃[16]。由于其建立在航空信息數字化基礎之上，則需要面向水平航跡進行規整和聚類，利用垂直剖面、速度剖面和高度剖面開展模型設計，從而實現對空間位置點精準預測[17]。另外，由于歷史雷達航跡存在空間重疊和飛行趨勢相似性的問題，在大范圍空間路徑識別和飛行環境衡量等問題上缺乏可靠的數學描述[18]，以及評價過程因數據類型欠豐富和特征不全面，導致4D飛行路徑計算結果無法對實際飛行正常性提供支撐[19]。

為解決上述問題，使用層次聚類優化動態時間規整算法，面向垂直剖面、各飛行階段速度剖面、高度剖面綜合設計評價模型，實現多數據歸類和特征分析，將進場航段各航路點飛行參數和空間位置數據作為采集對象，通過各剖面評價模型獲取偏差值，結合國際民用航空組織(International Civil Aviation Organization，ICAO)在飛行安全評價中對緩沖值(buffer value，BV)的設定，形成4D飛行路徑優化數據，實現基于4D飛行航跡規劃的空間位置點預測和路徑生成。

2 模型建立

由于歷史飛行、導航、軌跡等數據具有體量大、數據質量可靠性低、呈現方式存在區別等特性[20]，而且飛行軌跡因導航精度和運行環境的因素，存在收斂處理和偏差修正的需求，以規范其數學描述。根據數據分類進行預處理，利用基于層次聚類的動態時間算法(hierarchical clustering dynamic time warping，HCDT)、動態空間算法(dynamic spatial warping，DSW)、高度剖面優化算法(height profile optimization，HPO)，分別對各飛行階段下數據進行分析和處理，利用仿真實驗獲得飛行軌跡和時間維度結論，經計劃到達時間tPTA與預計到達時間tETA閾值比較，實現基于4D飛行路徑動態規整算法(4D dynamic warping，4DDW)構建的飛行路徑預測，4DDW規劃流程結構圖，如圖1所示。

2.1 水平飛行路徑規劃

通常情況下，整體空間內存在多個歷史雷達航跡，使用基于層次聚類的動態時間算法(hierarchical clustering dynamic time warping，HCDT)可實現精確計算和特征統一[21]，主要依據有兩點：①初始階段歷史軌跡數據類別較多，精確性較低，且隨計算量增加將出現誤差積累，導致計算結果失真，通過聚類優化的引入，可將導致誤差積累的因素進行分類，篩選獲得主要影響因素，為后續精準計算提供支撐；②因飛行速度不統一，飛行路徑距離或范圍不同，在時間軸上存在軌跡數據無法收斂，導致計算范圍不具有典型性，通過特征篩選和HCDT模型建立，將初始階段數據放在一個空間內進行比較，考慮其相似性，再將航跡視為時間序列并全局調整，實現時間序列長度統一，開展最優規整的比較，避免距離缺陷。

假設飛行路徑1為X，飛行路徑2為Y，由于研究空域范圍內的飛行路徑具有多樣化、復雜性特征，為獲取X與Y的規整路徑最優值，則有

W=w1,w2,…,wk

(1)

式(1)中：W為最優規整路徑，wk=(i,j)，數據越小表示飛行路徑相似性越高。例如，在第k條飛行路徑上用i和j表示其相似點。

如若存在相鄰飛行路徑長度為|X|和|Y|，則有

max(|X|,|Y|)≤k≤|X|+|Y|

(2)

式(2)中：K為相鄰序列拉抻長度情況，如圖2所示。

為保證相鄰飛行路徑1和2在空間數據中不重復，則規整路徑需從w1=(1,1)起至wk=(|X|,|Y|)結束，并滿足規整路徑wk=(i,j)中的i和j單調遞增，則有

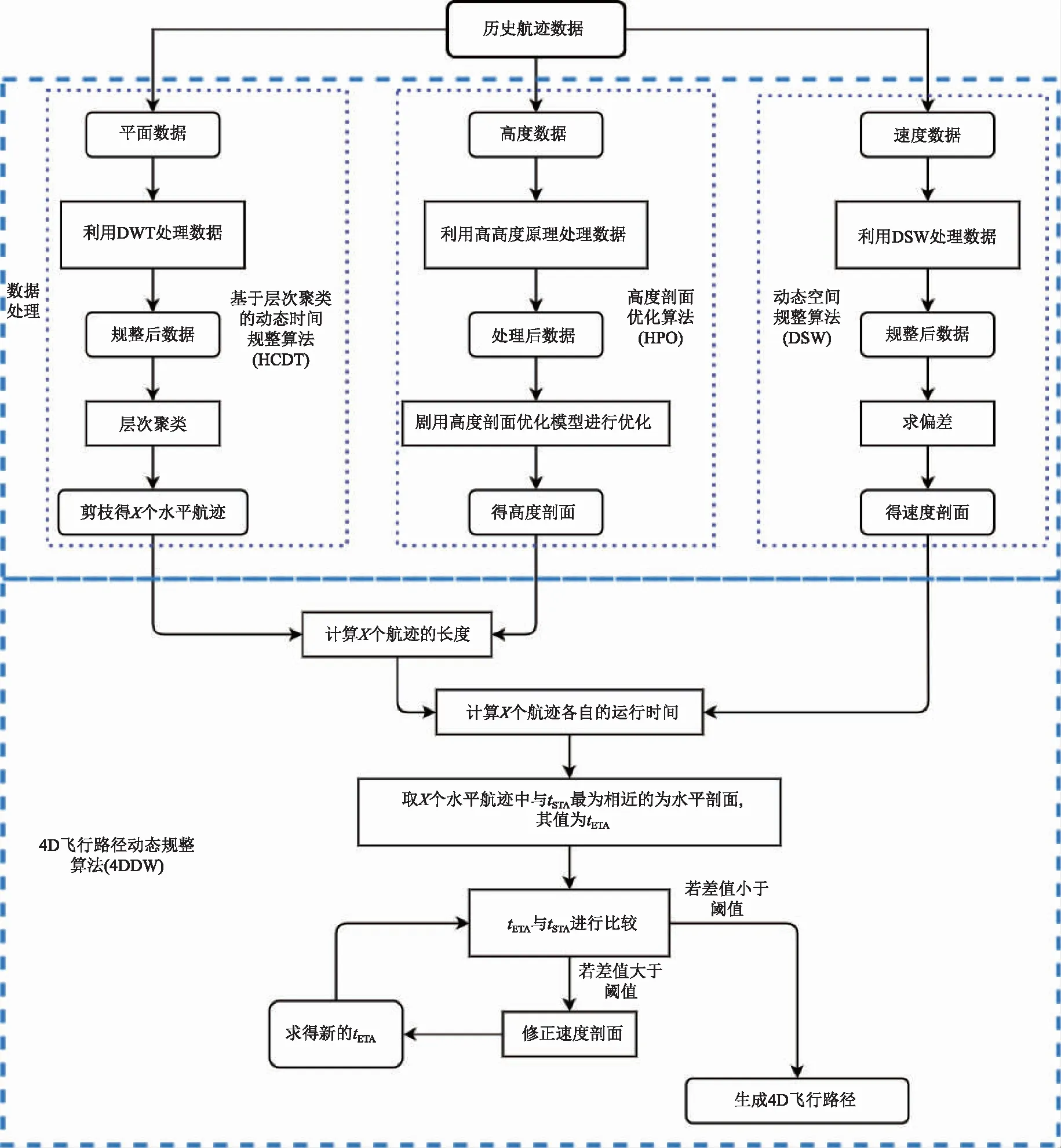
圖1 4DDW規劃流程Fig.1 4DDW planning process

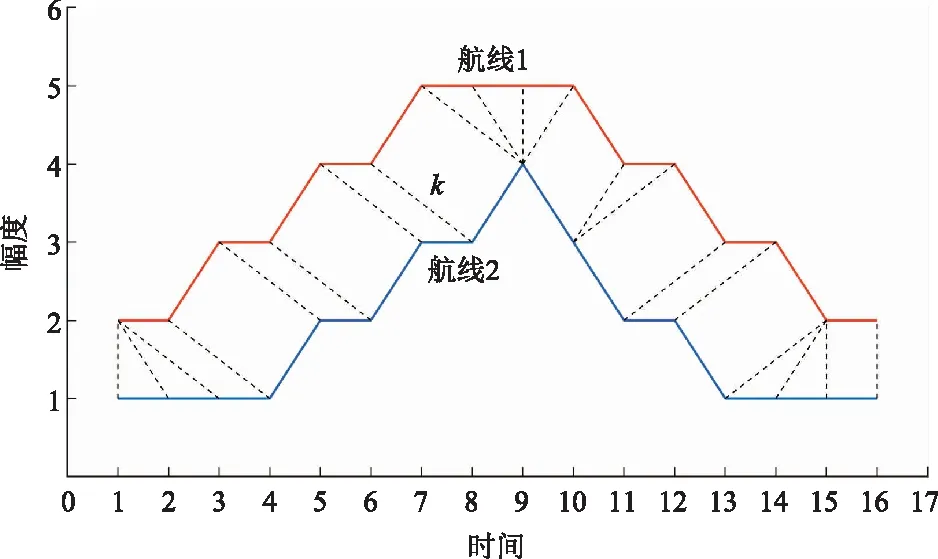
圖2 動態時間規整Fig.2 Dynamic time warping

wk=(i,j),wk+1=(i′,j′)，i≤i′≤i+1,

j≤j′≤j+1

(3)

如若路徑已存在wn=(i,j)，n=k，根據規整路徑基本原理，則(i+1,j)，(i,j+1)，(i+1,j+1)三式中，下一階段計算必選擇其一進行。那么對于規整距離D(i,j)，存在

D(i,j)=Dist(i,j)+min{D(i-1,j),

D(i,j-1),D(i-1,j-1)}

(4)

式(4)中：Dist(i,j)表示相鄰飛行路徑間i和j的距離；D(i,j)表示相似性衡量值，用于處理飛行路徑1在i之前的各個點，以及飛行路徑2在j之前各個點。

通過上述模型建立，可獲得規整路徑距離D(|X|,|Y|)，D越小則相鄰飛行路徑相似性越高，在水平方向上完成對飛行軌跡精準性和特征篩選問題上的處理。

2.2 標稱速度剖面設計

在速度剖面模型設計時，考慮了進場階段飛行路徑上各航空器機型和飛行性能，使用動態空間算法(dynamic spatial warping，DSW)并通過多個歷史雷達軌跡，建立速度剖面模型P，公式為

P={p1,p2,…,pn}

(5)

式(5)中：pi為第i架航空器在飛行中的速度剖面。整理P集合獲平均速度剖面，即為標稱速度剖面psta，表示數據集合中的均值，且滿足標稱速度剖面psta∈P，則有

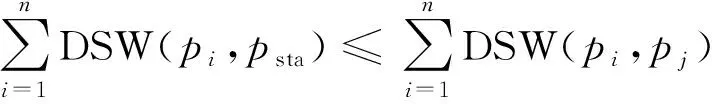
(6)

式(6)中：DSW(pi,pj)為動態空間距離，j可取任意值。

為提高航空器標稱速度剖面的精度可靠性，需要求所收集數據在時間序列上長度一致，通過序列相似性對比，通過增加采樣次數可提升數據長度一致性，從而實現對不同長度的時間序列進行有效比較。

設兩個速度剖面為

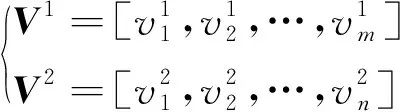
(7)

設A為速度剖面矩陣，開展數據對比，則有

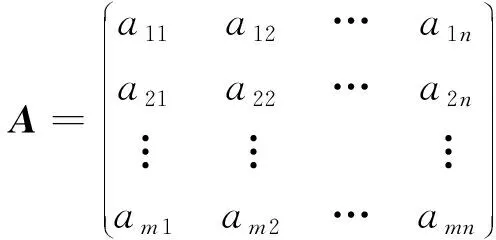
(8)

通過計算臨近速度剖面可獲得彎曲路徑，用W=(w1,w2,…,wk)表示，彎曲路徑需要滿足連續性、單調性和邊界條件，則有

(9)

DSW算法在極限路徑分析時具有保守性，適宜在飛行安全設計中應用，通過設置速度v1和速度v2間最小總距離，結合速度剖面矩陣，則存在

D(i,j)=a(i,j)+min{D(i-1,j),

D(i,j-1),D(i-1,j-1)}

(10)

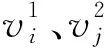
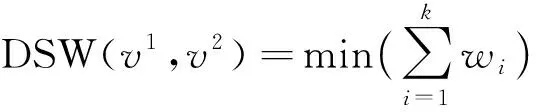
(11)

為進一步提升計算結果有效性，需逐一使用速度剖面進行DSW距離計算并且引入緩沖值BV概念，實現對各速度剖面偏差值的處理，以最小偏差值速度剖面構成標稱速度剖面，則存在

xi=BV+

(12)

2.3 高度剖面設計

在機場終端區飛行程序的儀表進近階段，連續下降運行(continuous descent operations，CDO)作為一個新穎的技術正在由ICAO進行推廣，CDO綜合考慮平飛段和最短下降段對提升空域使用率的影響，可有效改善運行標準，提升著陸階段的安全保障，則高度剖面模型采用CDO概念并進行設計。

根據CDO下降階段投影到地面距離最短的特性，建立高度剖面優化算法(height profile optimization,HPO)模型，即

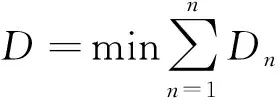
(13)

根據各下降階段高度對控制障礙物的約束特征，建立約束條件函數，即

Hon≥An+MOCn

(14)

由于航空器的著陸階段分為多個進近階段，且每個進近階段的最佳下降梯度要求各不相同，建立下降梯度限制函數為

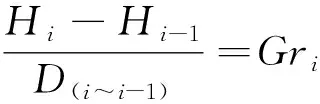
(15)

若此航段取最佳下降梯度且無關鍵障礙物限制，則

Di=D(i～i-1)=(Hi-Hi-1)/Gri

(16)

式中：Di表示第i個航段投影在地面的距離；Hon表示第n個障礙物處在航段的飛行高度；An表示第n個障礙物的高度；MOCn表示第n個障礙物所在地的最小超障余度(minimum obstacle clearance，MOC)；i表示航路點或定位點；D(i～i-1)表示i定位點到i-1定位點的距離；Gri表示i航段最佳下降梯度。

若此航段有關鍵障礙物限制，則不進行梯度優化。

通過將歷史航跡數據進行預處理和特征分類，利用HCDT、DSW和HPO進行模型建立和計算，可獲得初始多個水平航跡、高度剖面和速度剖面，為飛行航跡生成提供基本參數。

3 實驗設計

根據4D飛行路徑動態規整模型設計仿真實驗，具體如下。

(1)水平飛行路徑實驗：使用現有歷史雷達航跡進行動態時間規整，對規整后的結果進行層次聚類，運用層次聚類獲得的結果結合儀表進場航線，推導水平航跡數量和運行參數。

(2)速度剖面實驗：利用動態空間規整算法，對現有歷史雷達航跡上所獲得的速度剖面進行規整，計算選出偏差最小的速度剖面作為標稱速度剖面。

(3)高度剖面實驗：使用現有歷史雷達數據進行分析，整理空間內航路點的高度范圍，將水平航跡參數與整理后各航路點高度范圍進行結合，利用優化模型完成所對應的高度剖面設計。

(4)整理上述仿真實驗中水平航跡、速度剖面，以及高度剖面信息，計算獲得完整4D飛行路徑。

3.1 水平飛行路徑設計

采集實驗對象機場近180 d航跡數據為樣本，使用空客319為實驗對象飛機，對現有歷史雷達航跡進行時間規整和航跡聚類，建立現有歷史雷達軌跡樣本示意圖，如圖3所示。使用HCDT[式(1)～式(4)]對現有歷史雷達航跡進行規整，再使用層次聚類對規整結果進行聚類分析，具體結果如圖4所示。

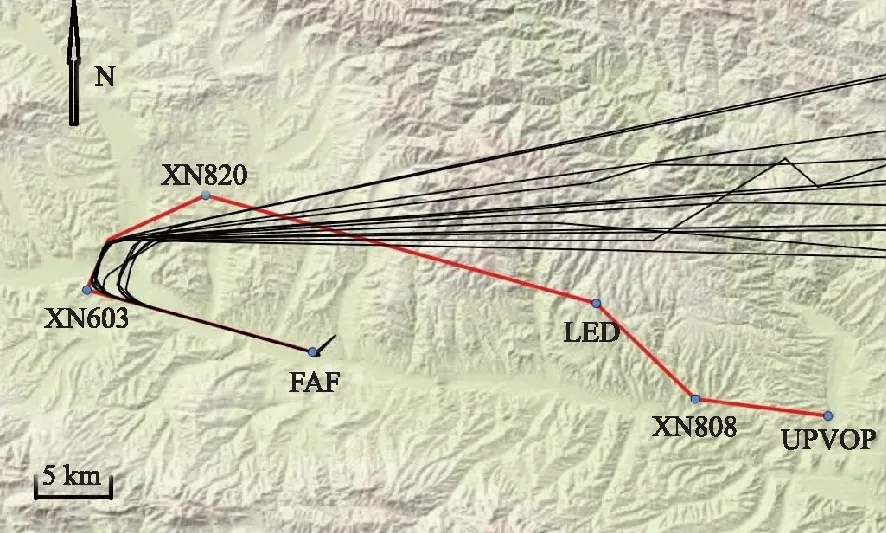
圖3 歷史雷達航跡Fig.3 Historical radar trajectory

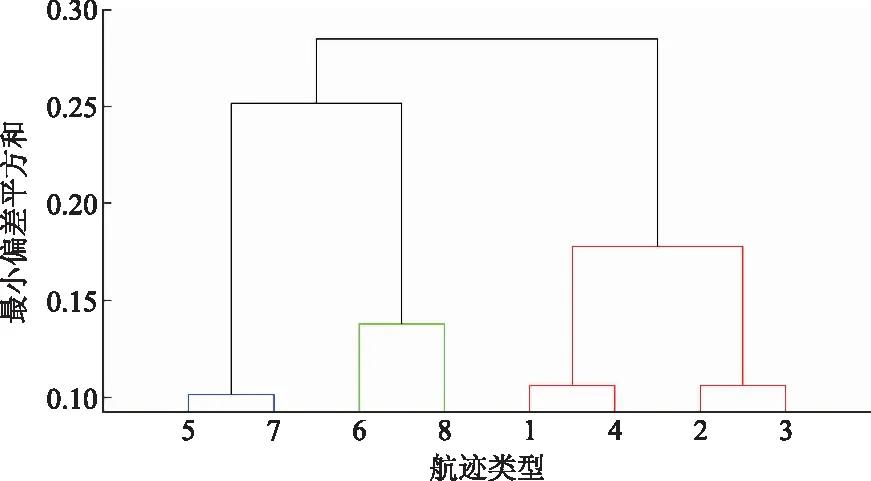
圖4 歷史航跡聚類結果圖Fig.4 Historical trajectory clustering result map

為使計算結果更為集中且具代表性，將最小偏差平方和設置為0.15×1010來對航跡聚類分析進行剪枝，將剪枝后的一個樹視為一個聚類，獲得4個航跡聚類結果，使用均值判定航跡聚類結果，對照實驗對象機場進場階段飛行程序，最終獲得4個水平進場路線設計，如圖5所示。

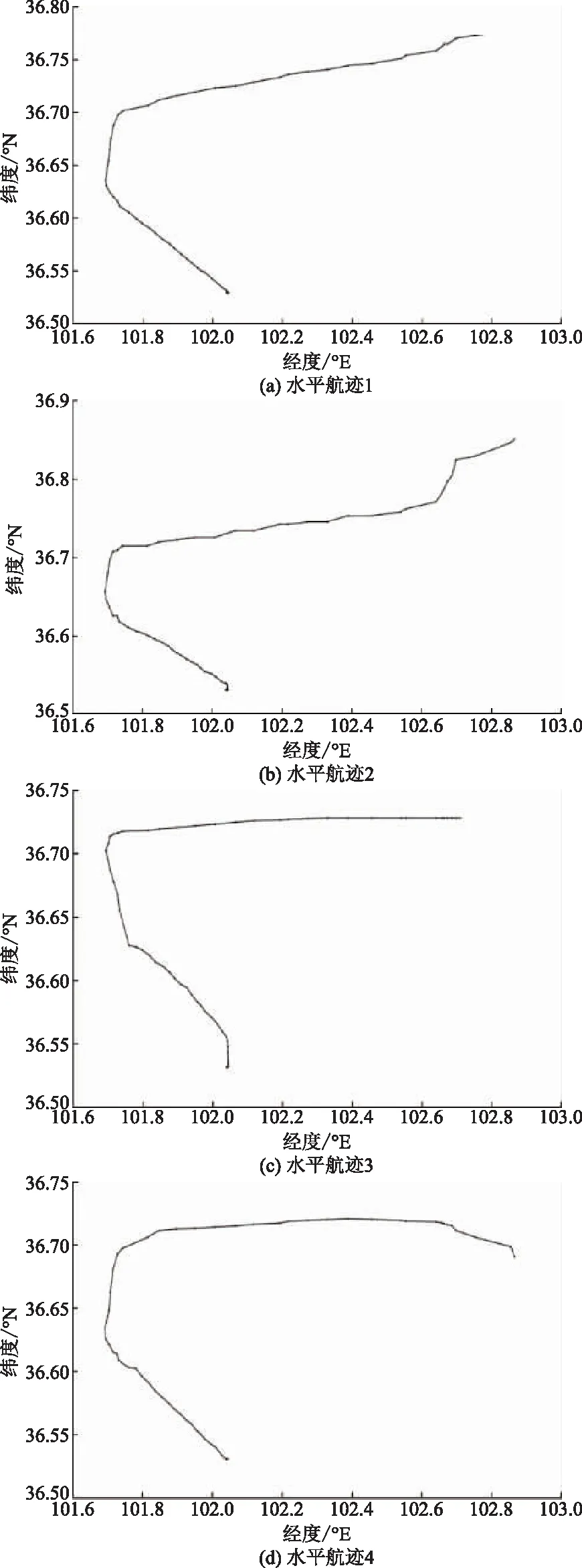
圖5 A1進場水平航跡Fig.5 A1 approach horizontal trajectory

3.2 速度剖面設計

選擇相同機場作為實驗對象機場，實驗對象飛機為空客319機型，采集現有歷史雷達航跡，篩選飛行速度、空間水平位置、飛行距離等信息，建立原始飛行速度剖面示意圖，如圖6所示。

根據速度剖面推導獲得DSW距離，通過式(12)對相關速度剖面進行偏差值計算，結果如表2所示。根據ICAO對飛行安全沖突值構建方式的建議，需在總系統誤差中引入緩沖值加以保守處理，則仿真實驗采用ICAO在進場階段的建議值，BV取1海里(n mile)。集合偏差值進行分析，依照保守原則取偏差極小值構成標稱速度剖面參數，由表2發現V4的偏差最小，則選取V4為標稱速度剖面，建立標稱速度剖面示意圖，如圖7所示。

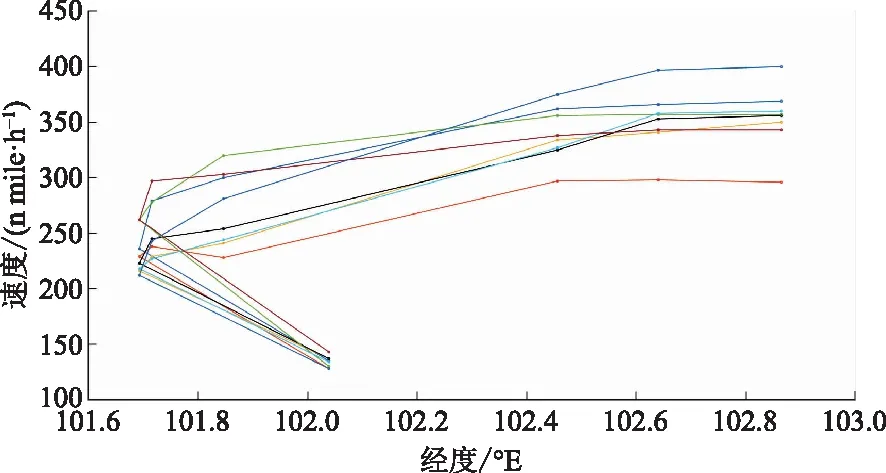
圖6 原始速度剖面示意圖Fig.6 Schematic diagram of the original velocity profile

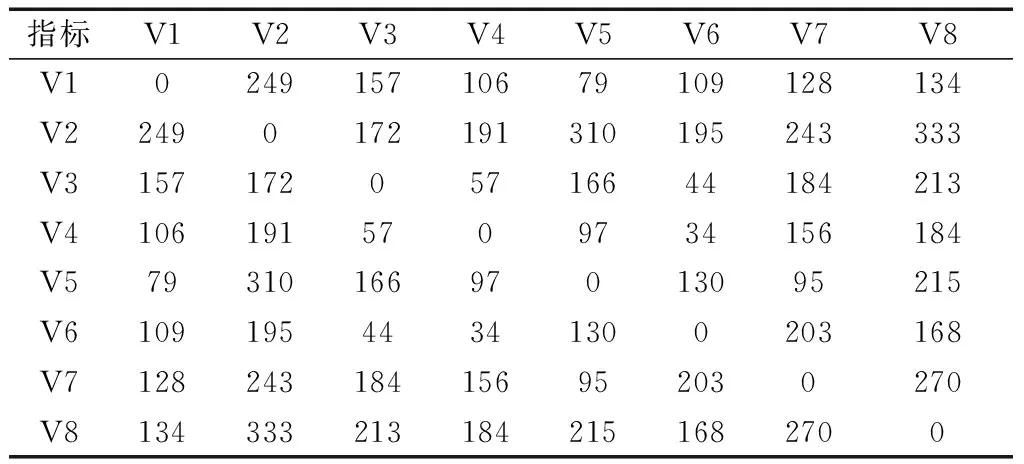
表1 DSW距離Table 1 DSW distance

表2 偏差Table 2 Deviation

3.3 高度剖面設計

選擇相同機場為實驗對象機場，采集進場階段歷史雷達航跡進行分析，獲得進場航空器高度范圍區間，如表3所示，建立高度剖面示意圖，如圖8所示。圖8中A6為起始進近定位點(IAF)，A7為中間進近定位點(IF)，A8為最后進近定位點(FAF)。

采集進場和進近階段障礙物數據，如表4所示。

按照ICAO對連續下降運行(continuous descent operations，CDO)的建議，利用HPO模型[式(13)～式(16)]對原始高度剖面進行優化，通過表4數據分析越障情況，設置進場航段最佳下降梯度為3%(<8%)，推導獲得優化結果，相關數據如表5所示，建立優化后高度剖面如圖9所示，其中A3為新增航路點。

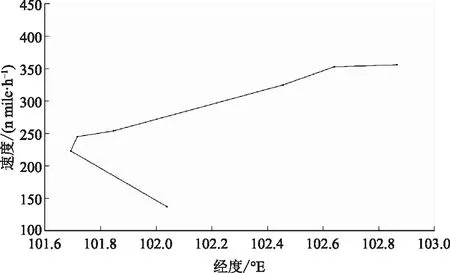
圖7 標稱速度剖面Fig.7 Nominal velocity profile

表3 各航路點高度范圍區間Table 3 Altitude range of each waypoint

ft為英尺,1 ft=0.304 8 m 圖8 高度剖面示意圖Fig.8 Schematic diagram of height profile

表4 障礙物數據Table 4 Obstacle data

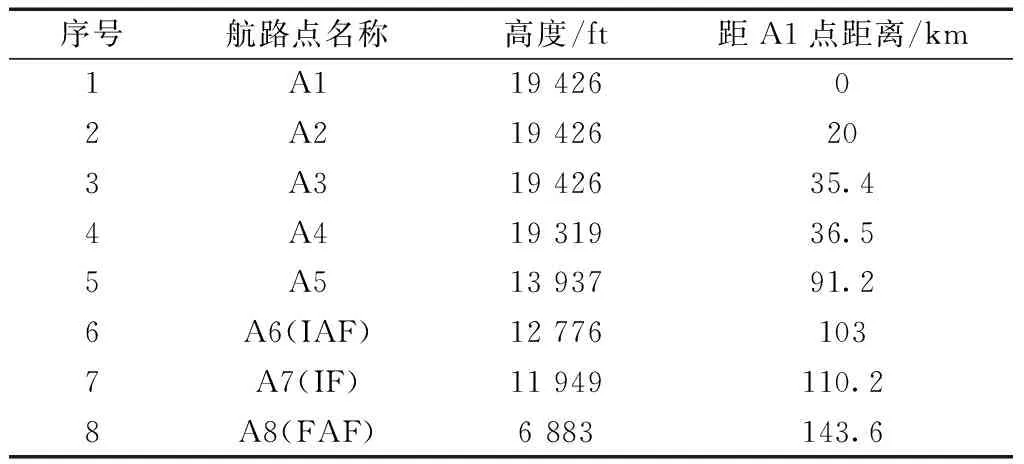
表5 各定位點高度與距A1點距離Table 5 The altitude of each anchor point and the distance from point A1

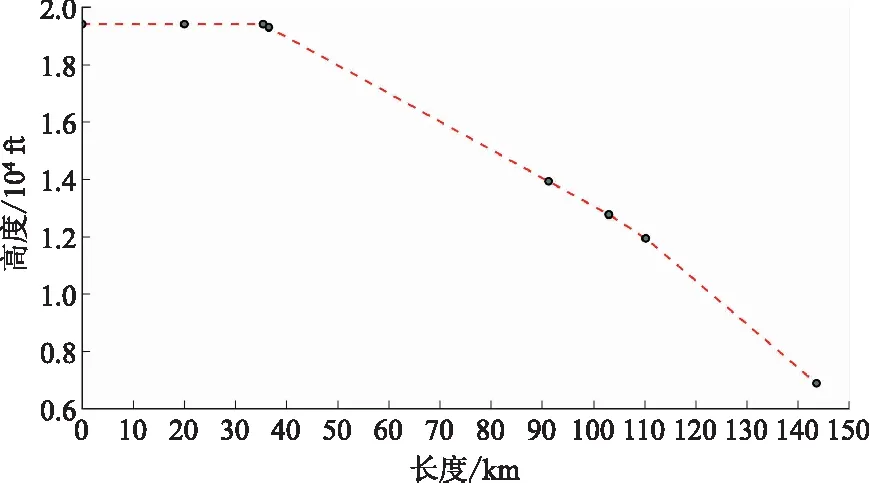
ft為英尺,1 ft=0.304 8 m 圖9 優化后高度剖面示意圖Fig.9 Schematic diagram of optimized height profile

通過圖8與圖9對比可以發現，使用高度剖面優化模型實施優化后，使平飛段距離增加35.4 km，且下降梯度持續處于飛行標準安全值以內，保證飛行安全，提升了飛行經濟性，符合約束條件的限制。

4 結果分析

根據水平航跡、速度剖面和高度剖面的實驗設計和計算結果，完成實驗對象機場由進場階段至進近著陸過程中的飛行航跡優化，計算獲得優化后航跡的所需飛行時間，選取4個典型優化結果形成距離和時間表，如表6所示。

根據優化結果開展計劃到達時間(tPTA)和預計到達時間(tETA)對比和分析，設置閾值為5 s，用以衡量4D飛行路徑的可靠性。結合表6優化結果分析發現，航跡4的飛行時間966 s與設定的飛行耗時(960 s)最相近，即tETA=966 s。計算tPTA和tETA的差值為6 s，超出預設閾值，因此對圖7所示的標稱速度剖面進行調整，修正后的速度如表7所示，修正后的標稱速度剖面如圖10所示。對照修正結果，使用標稱速度剖面和編號4飛行航跡進行分析，計算獲得飛行耗時為960.2 s，與tPTA所需飛行耗時960 s相差0.2 s，未超出預設閾值。在此結果之上，使用4D飛行路徑動態規整算法(4DDW)優化生成4D飛行路徑，利用歷史雷達航跡數據生成實驗對象機場進場航班原始飛行路徑，如圖11與圖12所示。

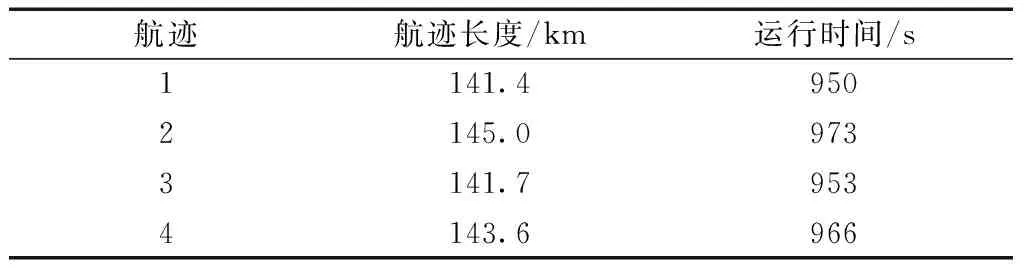
表6 典型飛行航跡和所需運行時間Table 6 Typical flight trajectory and required running time

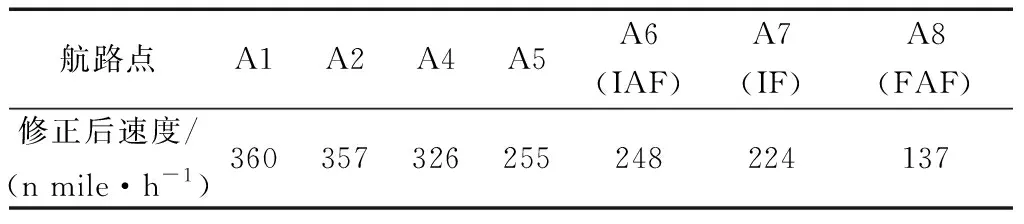
表7 修正后速度Table 7 Corrected speed

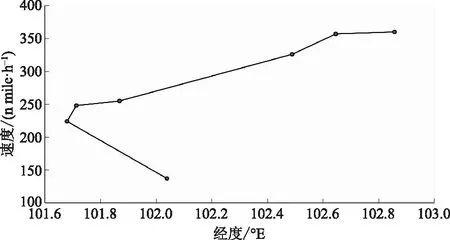
圖10 修正標稱速度剖面Fig.10 Correct the nominal velocity profile

ft為英尺,1 ft=0.304 8 m 圖11 4D飛行路徑規劃圖Fig.11 4D flight path planning diagram

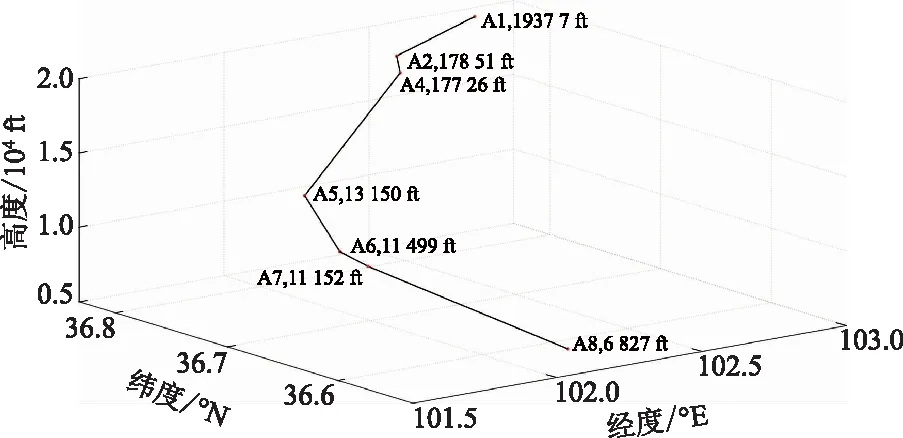
ft為英尺,1 ft=0.304 8 m 圖12 原始飛行路徑圖Fig.12 Original flight path diagram

根據仿真實驗結果對比發現，原始飛行路徑由A1起至A8點結束，其中沒有A3定位點，整個飛行軌跡未對時間維度進行規劃，而4D飛行路徑由A1起至A8結束，A3定位點為新增點并且在A3開始下降，從A1至A3為平飛段，使得4D飛行路徑可更靠近跑道，處于以較高飛行高度開始下降的姿態，提高了進場飛機機動性和經濟性。此外，4D飛行路徑在擁有時間維度的規劃后，可有效提升進場航班排序，提高飛行安全，減少終端區的沖突與擁擠。

5 先進性描述

現階段，相似研究主要集中在4D飛行路徑構建方面，對算法的便捷性和完整性考慮層級有差異，其中使用基于計劃到達時刻的四維航跡規劃算法較為常見，是普遍采用的典型算法。根據表3以及原始飛行數據建立仿真實驗，使用典型算法模擬生成4D飛行路徑，計算結果如圖13所示。

ft為英尺,1 ft=0.304 8 m 圖13 典型算法和4DDW的飛行路徑計算結果對比圖Fig.13 Comparison chart of flight path calculation results between typical algorithm and 4DDW

對比計算結果發現，在飛行姿態方面，4DDW具備平飛和下降階段，合理處理了越障安全和經濟性的關系。在飛行路徑結構方面，4DDW具備連續下降特征，優化了運行標準，提高了航空器飛行正常率。在空間路徑范圍方面，4DDW表現出空間范圍收斂的特征，為提升空域容量提供了基礎條件。

計算結果存在差異的原因有兩點：①因為構建4DDW算法的三個剖面，均考慮了時間維度規劃，使用了閾值預設和比較，使計算結果體現出對飛行時間和飛行距離的優化；②因為4DDW的高度剖面引入了CDO原則，將平飛、下降和越障分析加入到4D飛行路徑計算中，可優化運行標準和收斂空間范圍。由此可見，4DDW充分體現了在處理飛行路徑預測等問題上的綜合性和合理性，較當前常見算法具有先進性。

6 結論

通過仿真實驗和對比實驗計算結果分析，結論如下。

(1)4DDW依靠多維度模型對飛行各階段數據特征進行了梳理，使計算結果符合數據分類規律，使飛行環境衡量所需的數據類型和特征得到了豐富。

(2)4DDW依靠緩沖值和閾值的設計，使航空器空間位置點預測符合ICAO的飛行標準建議，為大范圍空間路徑識別提供了各位置點精準預測辦法，設置了相似性判斷依據，降低位置重疊概率。

(3)4DDW可為驗證現行有效飛行程序的科學性、合理性和經濟性提供依據，促進機場終端區飛行程序優化，保障飛行安全。