流動聚焦裝置微液滴生成及三維結構演化

王燕令， 張常青， 任敏， 劉鶴， 陳華， 吳學紅

(1. 鄭州輕工業大學能源與動力工程學院， 鄭州 450001; 2. 鄭州輕工業大學， 食品生產與安全河南省協同創新中心， 鄭州 450001)

液滴微流控技術是指在微米乃至納米尺度內控制微液滴流動的技術[1-2]，可廣泛應用于生物化學[3]、材料合成[4]、藥物研發[5-6]、醫療診斷[7-8]等領域。精確調控微流控芯片中的液滴生成可提高測試精度并加快反應速率[9-10]，因此，構建微液滴三維結構演化預測模型對精確調控液滴生產至關重要。

目前關于微液滴結構模型的研究多數是基于實驗結果進行預測，該類模型對于不同流型適用性并不高[11-12]。Cubad等[13]針對噴射流型和滴落流型液滴進行了間接實驗測量，認為液滴體積與分散相和連續相的流體物性、流動參數以及通道幾何形狀有關。崔藝文等[14]通過改變流動聚焦裝置中喉部長度和寬度實現對液滴體積的控制。鮑魯威等[15]通過對T形通道內的壓力測量，提出當分散相壓力大于連續相壓力時，通道生成液滴的體積更趨于穩定。Glawdel等[16-17]將液滴弧狀表面簡化為平面，對T形通道微液滴生成中擠壓流型進行了建模分析，該模型對于微液滴體積計算中易引起較大誤差。Chen等[18]基于截面形狀對液滴建立模型，同樣采用了Glawdel建模方法。Wehking等[19]假設液滴兩端由無數切片組成，其體積可以近似表示為液滴兩端的面積乘以切片的寬度，但該模型尚未實驗驗證。

此外，液滴微流控實驗采集的多是微液滴的二維形貌，其對應三維幾何結構特征的演化規律研究較少。構建合理的微液滴三維結構預測模型，對精確控制液滴體積大小非常必要。現基于多模塊分區建模思想，考慮微液滴斷裂階段和穩態過程的結構演化，提出一種描述流聚焦通道內液滴生成過程的三維幾何結構演化模型，該模型不僅適用于液滴尺寸大于通道寬度的擠壓流型，也適用于液滴尺寸略小于通道寬度的滴落流型和噴射流型。同時，基于實驗觀測結果進行模型優化，提升模型預測精度。

1 微液滴生成實驗測量

1.1 實驗系統

圖1為微液滴生成實驗裝置示意圖，實驗設備包括高精度注射泵(Centoni neMESYS)、微流控芯片、高速攝像機(PCO Dimax HS)、數據采集系統等。互不相溶的兩種液體(分散相和連續相)經注射泵分別進入微流控芯片，在流動聚焦區域內分散相被連續相擠壓從而生成液滴。

圖1 微液滴生成實驗裝置Fig.1 Experiment device of droplet generation

1.2 微液滴生成

聚二甲基硅氧烷PDMS(polydimethylsiloxane)與固化劑以質量比10∶1混合后，采用真空磁力攪拌器排出氣泡并混合均勻，澆筑于掩模版上，放置于真空干燥箱內，90 ℃加熱45 min后PDMS凝固，取出并切割打孔，經氧等離子體處理后與玻璃鍵合，經175 ℃烘烤4 h后取出靜置，使得微流控芯片通道轉變成疏水性壁面。實驗用微流控芯片分為兩組：上游孔徑wor=25 μm和wor=75 μm，實驗流動聚焦結構如圖2所示。

實驗中連續相采用低黏度礦物油(M5904，Sigma)，分散相是去離子水，兩相界面張力經測量為5.3 mN/m。圖3所示為三種分散相與連續相的體積流量比(Qd∶Qc=1∶1，Qd∶Qc=1∶2和Qd∶Qc=1∶4)下微液滴的生成，包括斷裂階段與穩態流動階段微液滴形狀。連續相流量分別為50、100、200 μL/h。采用ImageJ軟件對圖片進行測量計算。

圖3中顯示對于孔徑wor=25 μm的通道，當流量增加時，生成的液滴流型逐漸從擠壓流型轉變為滴落流型和噴射流型，對應的體積計算模型隨之發生變化。實驗同時測量了wor=75 μm通道內的微液滴生成，其規律與wor=25 μm通道類似。

圖2 實驗流動聚焦結構.Fig.2 Structure of the flow-focusing device

圖3 流動聚焦通道微液的生成(wor=25 μm)Fig.3 Droplet generation in flow-focusing device(wor=25 μm)

2 微液滴三維模型構建

2.1 微液滴流動聚焦生成過程形變演化

圖4為矩形截面通道內微液滴生成及其三維結構示意圖。互不相溶的兩種液體分別作為分散相和連續相流體，分散相流體Qd從左側進入通道，被上下通道內連續相流體Qc在流動聚焦區域擠壓斷裂，生成微液滴流出。圖4為擠壓流型微液滴生成實驗俯視圖，此流型下微液滴尺寸大于通道寬度。液滴生成后在微通道內流動，受最小表面能影響，其表面會收縮成半徑為h/2的圓弧。Glawdel借鑒T形通道微液滴結構預測模型[20]，指出流動聚焦微液滴的截面是由兩個r=h/2的半圓區域與中間矩形區域組成[14-15]，液滴體積計算可簡化為

(1)

式(1)中：Ap為圖4中液滴的投影面積；h為通道高度；l為液滴投影截面周長。

考慮到液滴在垂直高度方向其表面并非柱狀平直，而是有一定弧度的存在，通過式(1)計算得到的液滴體積整體偏大。微液滴生成過程中，其液滴穩態流型主要包括擠壓流型和滴落流型，模型如圖5所示。根據不同流量比下的液滴形狀，針對微液滴生成斷裂過程和下游穩態流動時其三維結構演變進行探究，建立了斷裂階段和穩態階段的數學模型，采用多模塊分區建模計算的方式，在模型計算時采用旋轉體積分方式，并修正錐形不規則斜面計算引入的計算誤差。

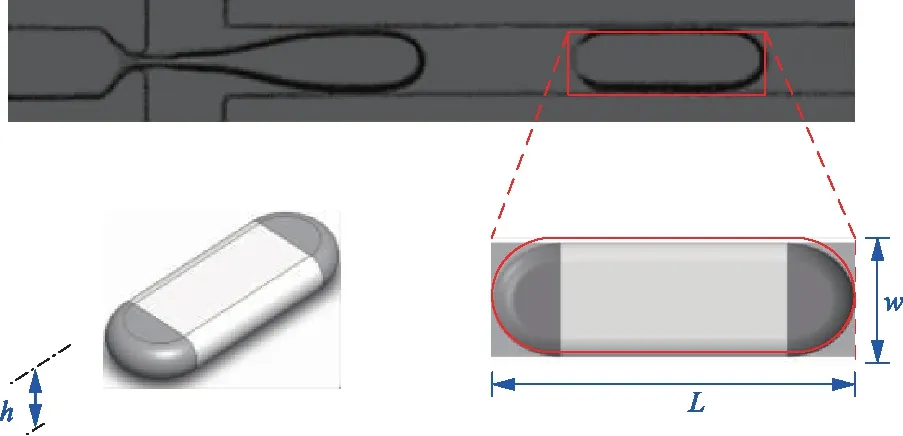
圖4 液滴生成及其三維結構Fig.4 Droplet generation and the three-dimensional droplet structure

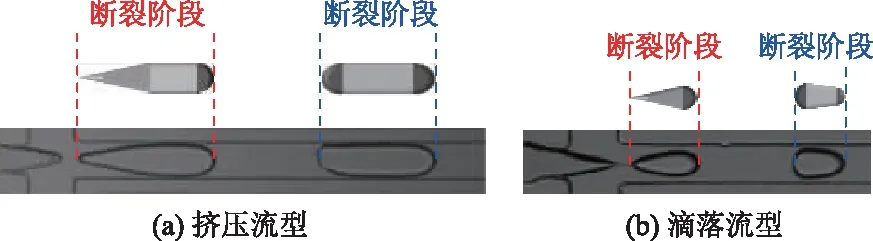
圖5 流動聚焦微液滴生成Fig.5 Droplet in the flow-focusing device

2.2 液滴斷裂階段三維結構演化模型

在微液滴斷裂截面，分散相液體受到連續相液體的擠壓作用，在主通道方向逐漸收縮至臨界直徑wpinch后斷裂。在較低的毛細數Ca下，液滴斷裂時剪切力影響較小，可以忽略。斷裂過程的主要驅動力是液滴前后的流動壓降。當液滴頸部與其頂部的Laplace壓力相等時，無法驅動液滴向前運動，上游分散相液體開始驅動液滴向下游運動，液滴斷裂。此時由Young-Laplace方程，有

(2)

式(2)中：Rneck為液滴頸部半徑；γ為界面張力。由于Rneck?wpinch，可得

(3)

由于液滴形狀受到通道幾何形狀限制，在通道壁面約束下液滴體積收縮成最小表面能的形狀，即r=h/2的圓弧狀。根據實驗測量結果，斷裂界面一般可以分為兩種情況：①當Qd∶Qc≤1∶4時，液滴內部包含一個平直拉伸段，即拉伸長度λ≠0，如圖6(a)所示；②當Qd∶Qc>1∶4時，液滴拉伸長度λ=0，此時液滴形似錐體，如圖6(b)所示。將斷裂階段液滴體積模型分為a～f共6個模塊：a部分為一圓臺，主要考慮到液滴頸部受力平衡時開始發生斷裂，其俯視截面與收縮段整體截面相似，b和c部分是傾斜的半圓柱，d部分是為三棱柱，e部分則是一個類橢圓柱體，其拉伸長度為λ，f是一旋轉體。表1給出了斷裂階段液滴a～f各分段模塊體積的計算方法和公式。

綜合表1，斷裂階段液滴體積為

V=Va+Vb+Vc+Vd+Ve+Vf

(10)

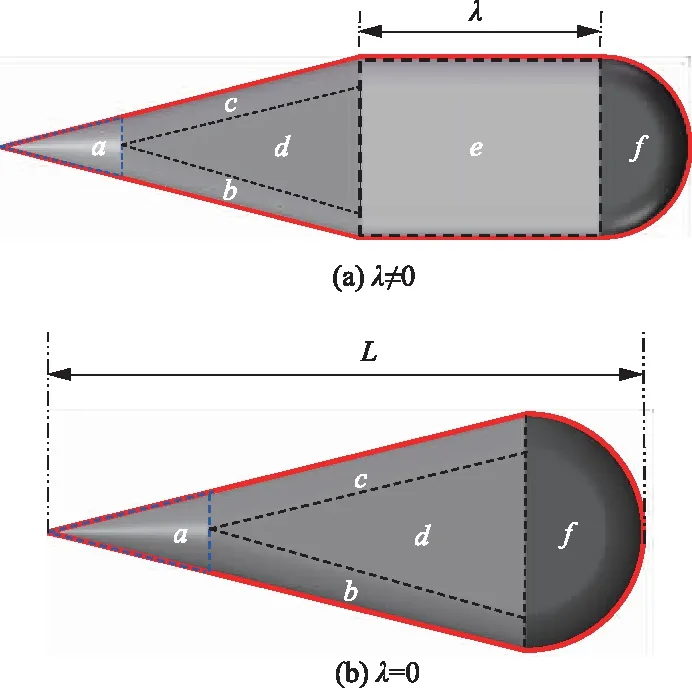
圖6 斷裂階段液滴體積模型分塊劃分Fig.6 Volume block model of the droplet at the breakup stage

表1 斷裂階段液滴體積分塊計算Table 1 Volume calculation of droplet blocks at the breakup stage

2.3 液滴穩態流動階段三維結構演化模型

液滴在下游流動時，連續相流體對液滴的擠壓作用已不足以引起液滴表面產生明顯形變，液滴前后兩端的形狀較為穩定。

根據實驗測量結果，穩態流動時一般可以分為兩種情況：①當連續相流量較大(Qd∶Qc≤1∶4)時，液滴中部是前后界面有一定傾角的楔型柱體，即θ≠0如圖7(a)所示；②當分散相流量較大(Qd∶Qc>1∶4)時，液滴傾斜角度θ=0，此時液滴尾部形狀收縮減小，如圖 7(b)所示。將液滴穩態階段其體積模型分為a～e共5個模塊：a和c部分均為旋轉體，e和d部分是半圓柱或傾斜半圓柱，b部分是為矩形或楔型柱體，定義前段寬度Dup，尾部寬度Ddown。楔型柱體傾角θ計算公式為

(11)

圖7 穩態流動液滴體積模型分塊劃分Fig.7 Volume block model of the droplet at steady flow stage

綜合表2各模塊計算可得，穩態流動階段液滴體積為

V=Va+Vb+Vc+Vd+Ve

(17)

表2 穩態流動階段液滴體積分塊計算Table 2 Volume calculation of droplet blocks at steady flow stage

3 模型驗證與優化

3.1 模型驗證

流動聚焦產生的微液滴在通道下游流動較為均勻，因此可以通過V=Qd/f來間接獲得液滴的真實體積，其中Qd為實驗設定的分散相體積流量，f為液滴生成頻率，其大小可通過高速相機捕捉統計。本研究以液滴等效半徑r來量化液滴體積的變化，其大小r=(3V/4π)1/3。

圖8所示為模型計算結果和實驗測量結果對比情況。可見，液滴斷裂階段，模型預測半徑r*與實驗液滴半徑r相對誤差δ為-11%～+17.5%，平均偏差為3.12 μm。其中相對誤差δ= (r*-r)/r，平均偏差AD=(∑|r*-r|)/n。此外，不同孔徑尺寸時，模型預測結果偏差也略有不同，wor=25 μm時計算顯示最大偏差為+6.69 μm，而wor=75 μm則是最大偏差-6.49 μm。引起預測結果偏差的主要因素是斷裂界面液滴在經歷臨界斷裂點時，界面張力急劇變化使得液滴出現明顯回縮現象，易造成液滴的測量長度整體偏小。當液滴處于下游穩態流動時，模型預測體積大小較實驗結果普遍偏小，相對誤差普遍分布在-20%～-35%，模型計算偏差趨勢受孔徑影響較小。綜合對比可知，對于斷裂階段微液滴大小和實驗測量值偏差較小，所構建的三維體積模型較為合理，能較準確描述斷裂過程液滴的形貌特征。而對于穩態流動階段液滴，構建的模型計算結果普遍偏小，可引入校正因子進行校正，對其三維模型加以優化。

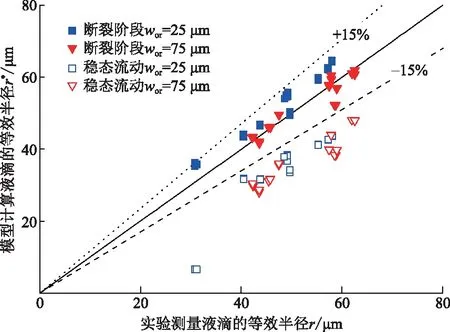
圖8 模型計算與實驗結果對比Fig.8 Comparison of the volume model with the experimental results

3.2 穩態流動模型優化

受制于工藝限制，實驗通道高度h均勻性難以精確控制，無法保證通道高度完全一致，導致液滴在通道內的真實長度難以反映在模型計算與實驗對比的基礎上，使得穩態流動模型計算數值普遍偏小，采用對穩態流動中間長度段進行修正，引入修正系數α，對式(13)、式(15)和式(16)進行修正，得

(18)

(19)

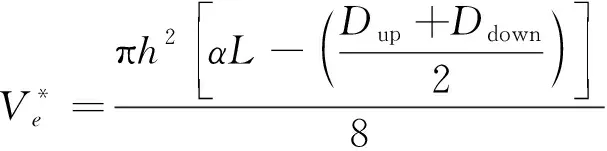
(20)

將修正后的公式代入計算表明，修正系數α=2.5時，模型偏差最小，如圖9所示。

圖9 穩態流動模型校正與實驗對比Fig.9 Comparison of the revised volume model with the experimental results for the steady flow

修正后模型預測半徑與實驗液滴半徑相對誤差在-15%～+19.7%，平均偏差為3.61 μm，相較修正前明顯改善。

4 結論

提出了描述流動聚焦裝置中液滴在斷裂階段和穩態流動階段的三維結構的方法，基于多模塊方式分段構建了液滴結構預測模型。基于液滴寬度w、液滴長度L、液滴流動傾角θ和液滴中間段長度λ四個基本參數來描述液滴的形狀和體積。模型考慮到液滴的三維曲面特征，利用分散相和連續相的質量守恒，可精確地預測液滴在形成周期中的結構特征。

對比液滴微流控實驗測量結果可見，液滴斷裂階段時，模型預測與實驗液滴半徑相對誤差δ在-11%～+17.5%，平均偏差為3.12 μm。wor=25 μm時計算顯示最大正偏差+6.69 μm，而wor=75 μm則是最大負偏差-6.49 μm。針對穩態流動模型偏差較大的問題，引入了修正系數α對模型進行優化，修正后液滴半徑相對誤差在-15%～+19.7%，平均偏差為3.61 μm，相較修正前明顯改善。