基于FTA-BN的危化品停車場槽罐車泄漏概率分析

王成龍，田宏，朱家鑫，賈圣孔

（沈陽航空航天大學 安全工程學院，遼寧 沈陽 110136）

由于化工行業迅速發展，危險化學品需求不斷增加，其運輸規模不斷擴大，并且以長距離的異地公路運輸為主。為了減少事故的發生，加強運輸車輛的安全管理，國內的化工園區、危化品倉儲物流等企業開始建設專用的危化品停車場。

危化品停車場中駐留的槽罐車裝載的危險化學品大多具有易燃、易爆或者毒害性，如果出現了泄漏的情況將伴隨著極大的危險隱患，容易產生爆炸、火災甚至是人員中毒事件，這也意味著將對停車場及周邊人員的人身安全帶來威脅，并可能會帶來相關的財產損失、環境污染等。

許多學者對危化品物流風險進行了一些研究[1-3]，這些研究大多集中在對道路運輸過程中的風險進行研究，且以定性研究為主，而對危化品停車場內部的風險研究得較少。本文針對危化品停車場內的槽罐車泄漏風險進行研究，借助于將事故樹轉化貝葉斯網絡的方法對危化品停車場中的槽罐車泄漏事故進行研究，目的是確定停車場內槽罐車的泄漏概率，以便對危化品停車場的風險分析和風險管理提供科學依據。

1 影響槽罐車泄漏的主要影響因素

駐留在停車場上的危化品槽罐車大多數是處于靜止狀態，儲罐的泄漏主要由儲罐本體和管路系統兩大問題導致。

造成槽罐車儲罐泄漏的主要因素有兩點，其一是部分儲罐存在質量不合格的情況，其二是由于長時間的使用導致儲罐本身的儲存強度削弱，即造成了罐體疲勞。

儲罐自身的質量不合格主要是由于設計制造的問題造成的，罐體疲勞主要是由于超裝和超壓這些違規因素造成的，其中環境溫度過高以及安全附件失效是引起超壓的主要因素。當管路系統出現泄漏的問題時，往往表現為管道破裂、閥門失效或是法蘭無效密封[4]。

影響儲罐泄漏的影響因素還包括人的因素。其中，如果操作人員沒有按照規范的操作流程進行，或者是出現違規操作，可能會導致罐體出現泄漏。除此之外，在維護方面，維修人員對槽罐車設備故障檢維修不及時，這些都可能導致事故的形成和發生[5]。

此外，安全檢查制度的不健全以及不能嚴格貫徹執行也是導致儲罐泄漏的影響因素之一。

基于以上分析，以危化品停車場槽罐車泄漏作為頂事件，建立的事故樹如圖1所示，事故樹中符號所對應的事件如表1所示。

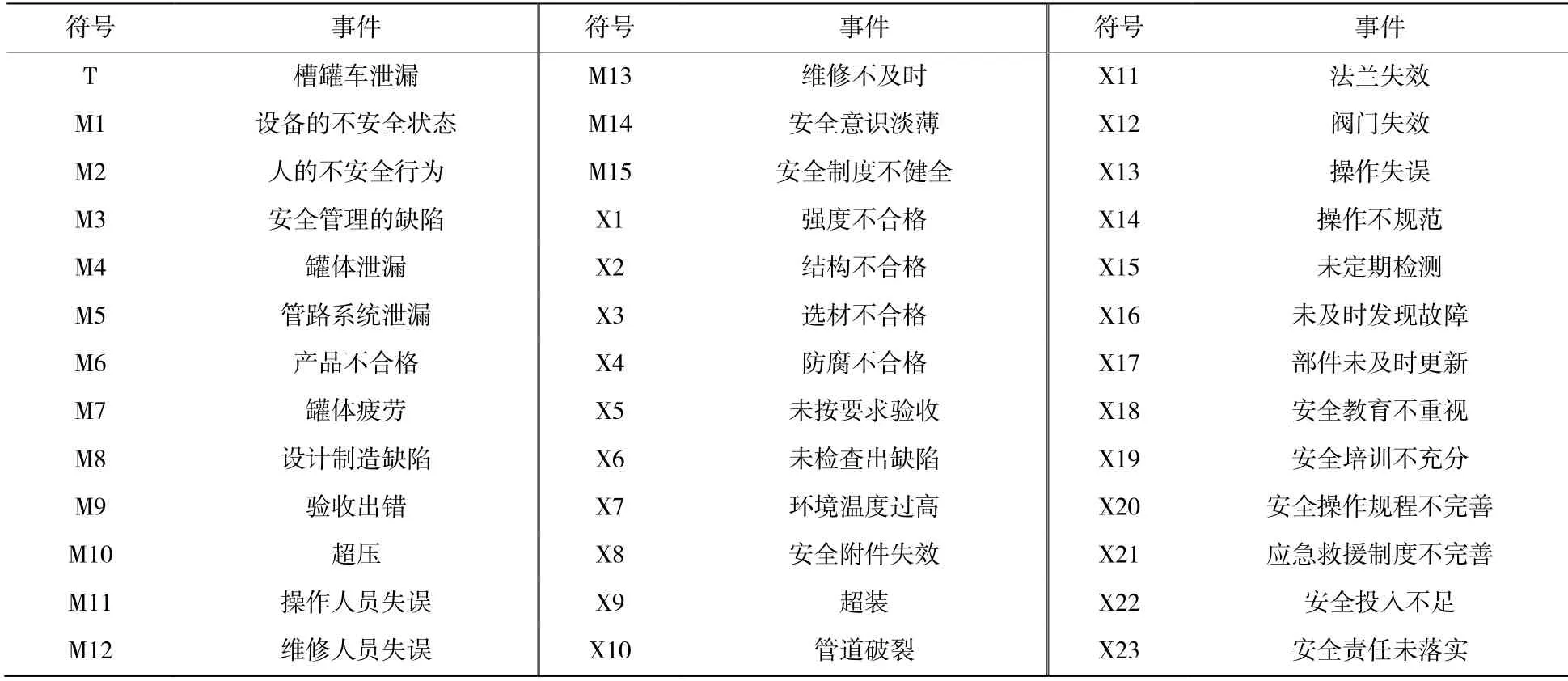
表1 危化品停車場槽罐車泄漏事故樹的事件和編號

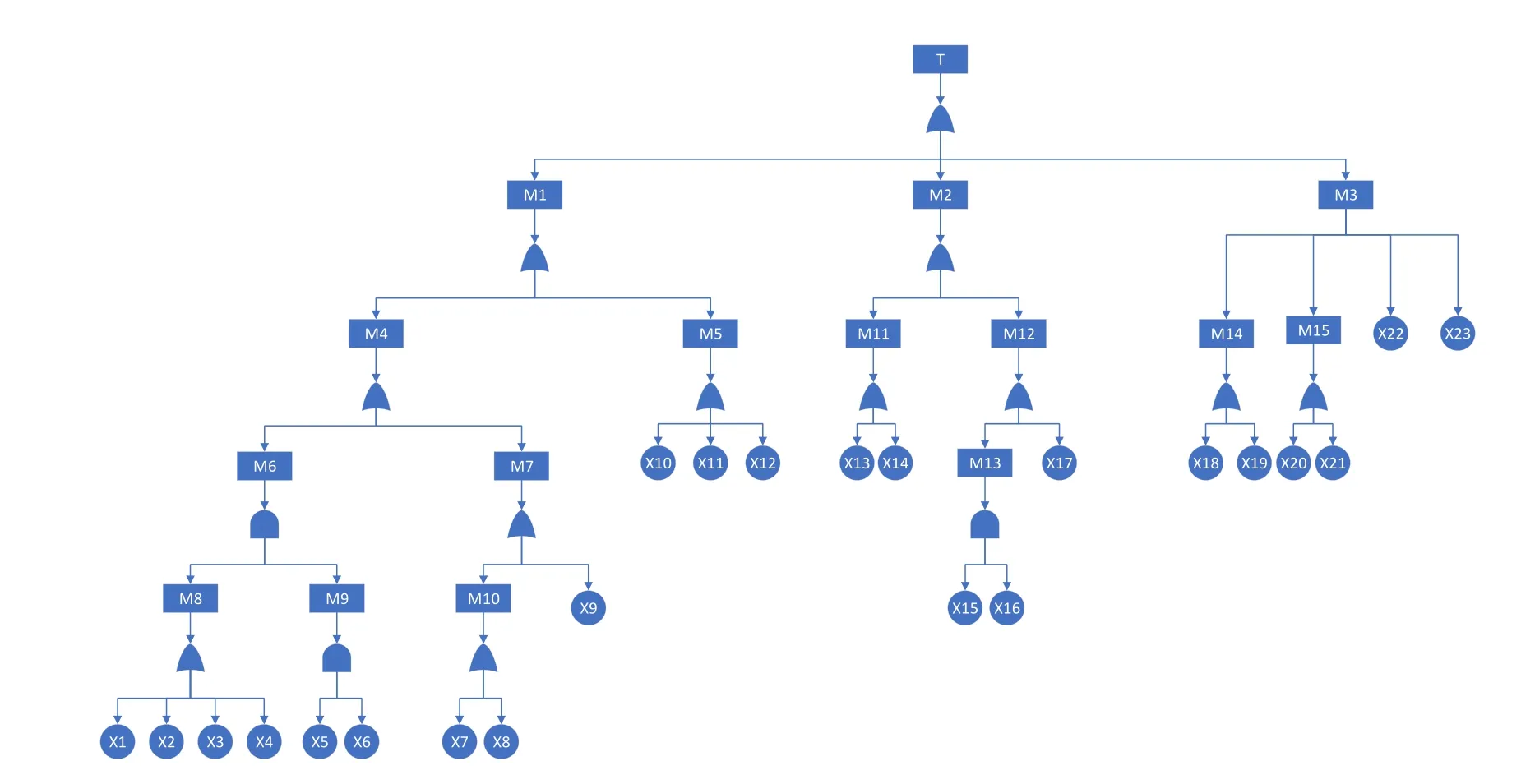
圖1 危化品停車場槽罐車泄漏事故樹

2 模糊貝葉斯網絡以及槽罐車泄漏概率分析

影響槽罐車泄漏概率的影響因素很多，很多具有模糊性且難以量化，一般的數學方法難以處理。貝葉斯網絡能夠充分利用定性知識和定量數據以及本領域專家的經驗和知識對影響槽罐車泄漏的影響因素進行推理分析，最終得到槽罐車的泄漏概率。使用貝葉斯網絡對槽罐車泄漏概率分析主要包括以下3 個步驟：①基于槽罐車泄漏事故樹利用GeNIe軟件建立對應的貝葉斯網絡模型；②基于三角模糊數根據專家經驗和知識對根節點進行模糊化處理；③對模糊化的數據進行解模糊得到模糊可能性值并將模糊可能性值轉化為模糊失效概率，最后通過GeNIe 軟件將得到的模糊失效概率進行演算分析從而獲取罐體泄漏的概率。

2.1 貝葉斯網絡

從概念上來看，貝葉斯網絡（BN）指的是通過有向無環圖來表現出要素之間依賴關系的網絡結構，這種網絡結構主要由有向無環圖（DAG）若干個條件概率表（CPT）組成，可以表示為：

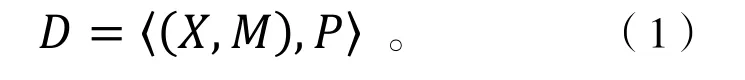
其中，(X,M)是具有n個節點的 DAG；M是這些節點的有向邊；其中的每一個節點都代表著一種隨機變量，X ={X1,X2,…,Xn}則是隨機變量的集合；DAG 的組成包括這些節點及實現這些節點連接的有向邊；P 是每個節點上的 CPT，即代表著一組對應的條件概率。DAG 通過定性的角度描述了貝葉斯網絡的整體結構，CPT 則是通過定量的角度描述了貝葉斯網絡的參數，即在父節點的所有取值組合下，某一節點處于不同的安全性影響因素狀態的條件概率，同時，根節點的先驗概率值代表著處于不同狀態的概率[6]。

BN 的聯合概率分布式為：

式中：π(Xi)表示—Xi的父節點。

2.2 事故樹向貝葉斯網絡映射

通過事故樹向貝葉斯網絡映射的方式能夠通過利用歷史信息，從而降低建模難度。通過事故樹模型來構造貝葉斯網絡的過程主要包括兩個板塊：①首先明確貝葉斯網絡有向無環圖，需要將網絡中的各個節點與事故樹的各個時間分別對應，并通過有向邊連結對應的節點;②明確條件概率參數，把事故樹中的邏輯門轉化為貝葉斯網絡的節點條件概率分布，如圖2所示，具體流程見圖3。根據前面對于危化品停車場所建立事故樹模型，利用上面做介紹的流程，利用GeNIe 軟件建立危化品停車場槽罐車泄漏的貝葉斯網絡模型如圖4所示。

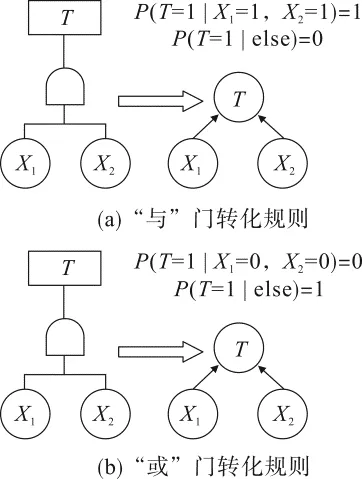
圖2 FTA 向BN 的轉化規則

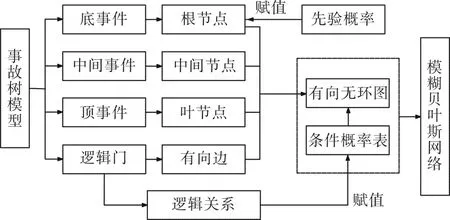
圖3 基于FTA 構造BN 流程

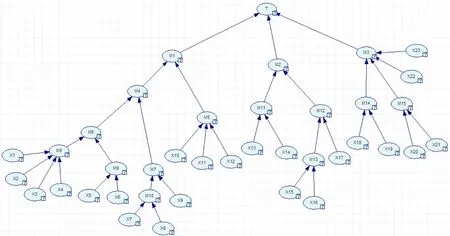
圖4 危化品停車場槽罐車泄漏的貝葉斯網絡模型

2.3 槽罐車泄漏概率的模糊解法

本文中在基于貝葉斯網絡來對于槽罐車泄漏概率進行分析的過程中有一個重要前提就是根節點與中間節點的概率均需為單一且精確的數值。然而，在槽罐車泄漏事故中出現的影響因素較多，從而具有一定的多態性與不確定性，使用傳統計量方法難以得到對于本事件概率的精確量化結果。因此，本文將進一步對于底事件的模糊性問題進行探究，由此引出三角模糊數求解的方式。

2.3.1 三角模糊數

三角模糊數記為 A=(a,b,c)，其隸屬度函數為[7]：

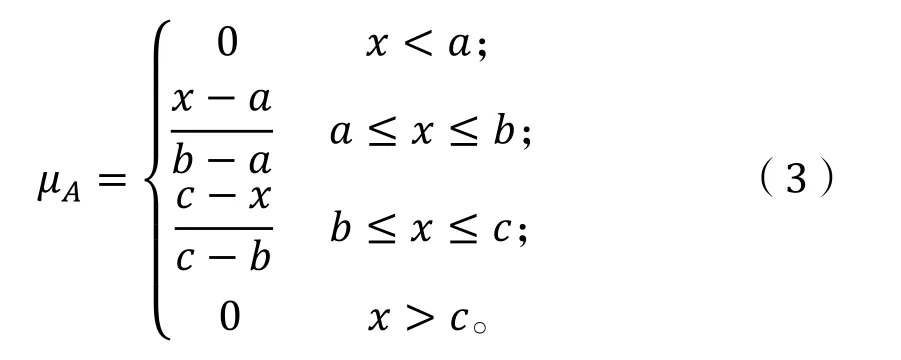
任取λ=[0,1]，則Aλ={x ∈R,μA≥λ} =[AUλ,ALλ]，Aλ為A的λ-截集。

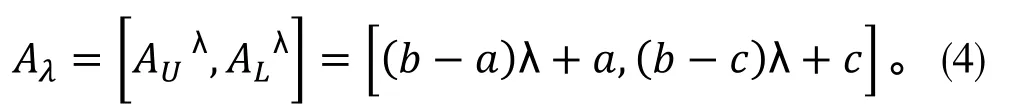
2.3.2 解模糊

通過解模糊的方式能夠將各事件發生過程中的模糊可能值轉換成精確值。根據LIOU[8]的積分值方法，可以通過λ-截集的運算處理模糊數，LIOU 的方法具有基礎且可操作性，因此在本文中將采取此方法來進行處理，主要計算公式如下：

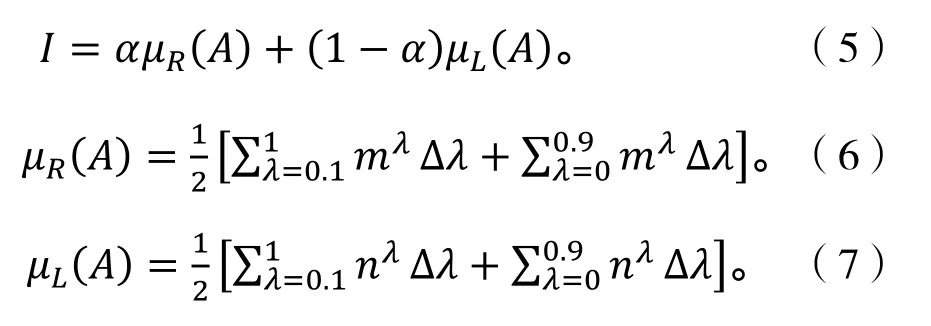
I表示模糊可能性的代表值；α∈[0,1]，代表樂觀系數；α =0、α =1，分別對應解模糊數A得到的模糊化值的上、下界；α =0.5 時，為模糊數A解模糊化值的代表值；μR(A)、μL(A)分別代表模糊數左、右隸屬函數反函數的積分值；mλ、nλ表示模糊數A的λ-截集的上下界，=0,0.1,0.2,…,1，，Δλ=0.1。

2.3.3 模糊失效概率

由于在計算過程中采用模糊數代替基本事件發生的概率使得發生概率的真實數據與事件發生的模糊可能性存在一定程度的差異，所以通過將模糊可能性向發生概率的轉換工作可以有效解決這一狀況[9]，ONISAWA[10]的研究可以有效完成這一轉換工作，計算過程如下：

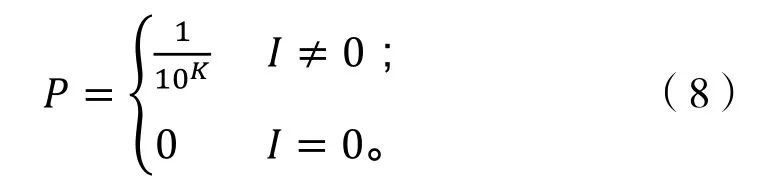
式中K為轉化系數：

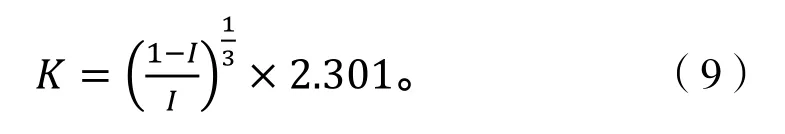
3 實例研究

目前，對于罐車的失效概率沒有數據庫可供利用，此外有些因素，尤其是管理因素也難以量化。因此，本文嘗試通過專家評判的方法來評判圖1中事故樹中基本事件發生的概率。專家評判語言集共分為5 個等級，按順序依次為“低”“低”，“中等”“較高”“高”，可利用三角模糊數對專家語句進行轉化。發生概率語言描述對應的模糊數形式和λ-集見表2，其中，率語言描述對應的模糊H”表示“低、較低、中等、較高、高”。

表2 發生概率語言描述對應的模糊數形式和λ-截集

以X8 為例，4 位專家分別給出的評價結果依次是：“較低”“較低”“較高”“中等”。然后，為了得出更精準的發生概率，本文將基于4 位專家的評判結果進行綜合評判進而計算出 X8 的平均模糊數，計算過程如下：

根據公式（5）、公式（6）、公式（7）得：

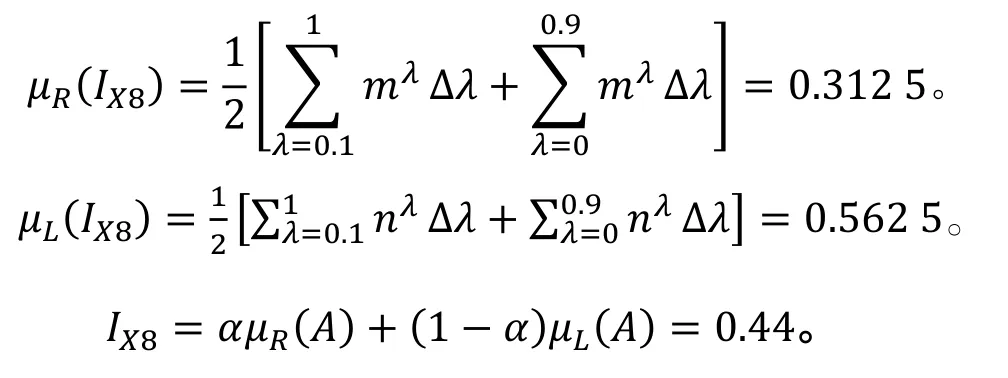
根據公式（8）、公式（9）得：

P(X8)=0.003 2。

同理可得其他根節點概率如表3所示，將經過分析后的數據進行整理輸入到GeNIe 軟件中得：P(T=1)=0.144 2，即該危化品停車場槽罐車泄漏概率為0.144 2。

表3 根節點概率表

4 結束語

本文首先基于事故樹找出導致槽罐車泄漏的原因，進一步通過貝葉斯網絡的條件概率計算方法演算出事故發生的概率，在整個過程中一定程度上解決了本文探究的影響槽罐車泄漏的影響因素的量化問題，并在探討過程中充分考慮并降低了使用事故樹分析過程中出現的不確定性和模糊性。

本文在探究過程中也存在著一定的缺陷，值得未來進行深入思考。本文中只基于導致事故產生的因素進行分析，而未進一步的揭露各風險因素之間的作用關系。因此，在未來的探究過程中，應該結合案例情景進一步分析危化品停車場槽罐車泄漏事故在不同的場景下的數學期望值，最終得出最容易導致事故的場景并提出相關建議。