聚焦本質(zhì)，多維辨析促思維

陳嵩

（福建省廈門市群惠小學(xué) 福建廈門 361003）

學(xué)生在六年級學(xué)習(xí)圓周長和面積時，經(jīng)常出現(xiàn)求“周長”變成求“面積”。筆者在六年級上冊教完圓的周長后，馬上測試求一個半圓形的周長。

題目：把一張半徑是5厘米的圓形紙片對折，得到一個半圓，這個半圓的周長是多少？

這道題目的測試結(jié)果相當(dāng)驚人，整個年段正確率不足30%，幾乎都錯在沒有加一條直徑這個典型錯例上。很多學(xué)生對周長的認(rèn)識僅僅停留在描述性概念這一表面上。到底什么是“圖形一周的長度”，甚至什么是“圖形的一周”，學(xué)生對這些問題的認(rèn)知是缺失的。

周長的概念首次出現(xiàn)在三年級。下面筆者就以三年級“認(rèn)識周長”一課為例，談?wù)勅绾位趯W(xué)情，單元整體備課，上下勾連，深化知識的內(nèi)在結(jié)構(gòu)，以多維活動為載體，呈現(xiàn)問題鏈化解學(xué)生的困惑點、易混點，讓學(xué)生在體驗中去辨析、梳理、評價，發(fā)展其高階思維能力。

一、精準(zhǔn)前測，暴露困惑點和易混點

三年級上學(xué)期的學(xué)生，處在直觀動作思維向抽象邏輯思維發(fā)展的過渡階段，也是從認(rèn)知一維圖形（線段、直線等）過渡到認(rèn)識二維圖形的階段，這需要大量感性表象和實際操作的支撐才能理解抽象的概念。認(rèn)識周長是在學(xué)生認(rèn)識了四邊形、三角形等圖形，并在二年級學(xué)會了測量長度的基礎(chǔ)上進(jìn)行教學(xué)的，充分利用這些基礎(chǔ)知識，才能讓學(xué)生理解周長的概念和測量各種圖形的周長。

那么，學(xué)生對周長的認(rèn)知水平如何？是否有意識地利用工具來測量周長？筆者設(shè)計了如下調(diào)研問題：

1.你聽說過周長嗎？請結(jié)合生活用圖畫與文字來表示你對周長的認(rèn)識。

2.下面的圖形或物體有一周嗎？有的請打鉤并把它的一周描出來。

3.在下面點子圖中，1號圖形和2號圖形的周長相比誰大誰小。

調(diào)研結(jié)果顯示，班級52人只有8人能圍繞“周”或“長”描述。這種題目是一個很常規(guī)的問題，可見，高年級學(xué)生雖然會描述相關(guān)概念，但是對本質(zhì)的理解是欠缺的[1]。

調(diào)查應(yīng)反映學(xué)生認(rèn)知的知識本質(zhì)的盲點。基于這樣的思考，上述調(diào)研題目也無法判斷學(xué)生是否有利用工具來測量長度的意識。筆者進(jìn)行了第二次調(diào)研，題目如下。

（1）下面的圖形或物體有一周嗎？有的請在（）打鉤，并把它的一周描出來。

（2）下圖有一個長方形和一個正方形，你能用什么辦法知道哪個圖形一周的長度更長？

（3）下面的點子圖中，1號圖形和2號圖形周長相比（）（一樣長或誰更長？）

結(jié)果顯示，學(xué)生對一周的概念不理解，容易受面的干擾；超過半數(shù)學(xué)生懂得借助工具測量，但大部分學(xué)生只測量出圖形部分邊線長度。由此可見，周長對學(xué)生來說比較抽象，會受到二維平面的影響。如何消除這種影響讓周長可視？部分學(xué)生不理解 “一周”，如何幫助理解含義，并在活動中滲透度量思想？

學(xué)生在前測暴露的困惑點和易混點，有助于教師聚焦問題的核心。在教學(xué)中，教師應(yīng)著重幫學(xué)生突破“一周”認(rèn)知的困難，引入“邊線”，借邊線感受一周，將一周從二維平面上剝離出來，讓其可視，排除了面的干擾后，再聚焦下一個難點——周長的度量。在學(xué)生測量一周的長度時，將借助格子圖點子圖的單位度量，去溝通計算方法。

二、整合教材，上下勾連抓本質(zhì)

筆者梳理了小學(xué)階段十二冊內(nèi)容中圖形測量部分的知識點，發(fā)現(xiàn)圖形的測量包括初步感知、一維測量、二維測量、三維測量。學(xué)生在這之前學(xué)習(xí)了長度單元，并體驗了統(tǒng)一長度單位的重要性。單元整體備課有助于對圖形測量部分的縱向梳理。由此明確：周長是小學(xué)周長學(xué)習(xí)的第一課時，也是小學(xué)階段第一次利用長度單位直接度量，是勾連一維度量和二維度量的通道，學(xué)生一維度量的意識又會影響到二維和三維度量，所以認(rèn)識周長在教材中的重要性不言而喻。

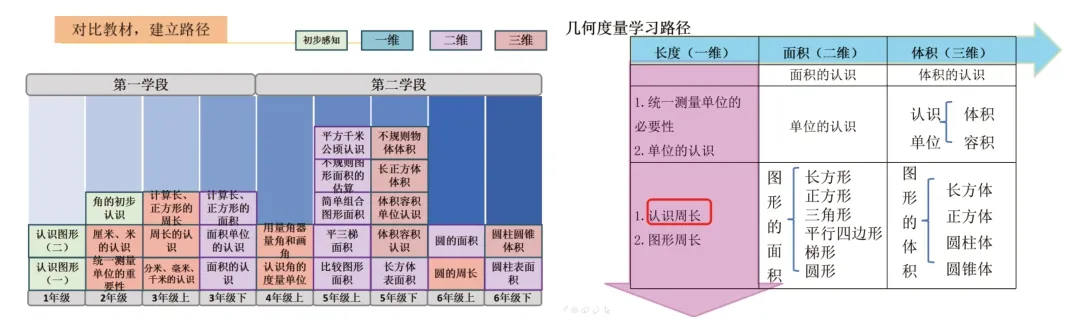
筆者將周長定義為二維圖形中的一維概念，它的本質(zhì)就是一維長度的度量。低年級的學(xué)生會測量一條給定線段長度，為什么高年級的學(xué)生反而不會求這些線段的長度（周長）呢？這個問題出現(xiàn)在學(xué)生從一維圖形過渡到二維圖形認(rèn)識的過程中。當(dāng)一條線段首尾相接的時候，這條“線”就消失了，學(xué)生眼里只看到這個圖形的“面”了。對邊上“線”的感知就降低了，圖形的“一周”當(dāng)然就消失了。

通過對比北師、蘇教、人教版教材，筆者又發(fā)現(xiàn)，北師大版和蘇教版的教材都有說到這條線，北師大版是讓學(xué)生用彩筆描出樹葉一周的邊線，而蘇教版則是指一指書簽一周的邊線，無論是畫還是指，都是在借助“邊線”讓周長直觀可見，通過對比分析，在周長一課的設(shè)計中引入“邊線”，其目的是讓周長可視。所以如何讓這一周重現(xiàn)，讓周長可視，就是備這節(jié)課的突破口。

三個版本的教材，其整體教材編排順序一致，但在教學(xué)路徑上，北師版由特殊（身邊的物體）到一般（圖形），人教版蘇教版是由一般到特殊。不同的教材的核心活動都是突出動手操作和探究這些學(xué)習(xí)方式，這樣安排的目的都是為了培養(yǎng)學(xué)生的度量意識，所以度量意識就是核心活動的重中之重了。

基于以上分析，在教學(xué)上應(yīng)注重抓“本質(zhì)”，周長是封閉圖形一周的長度。這樣的描述中，“一周”是一個空間概念，是周長概念中形的本質(zhì)，而“長度”是一個數(shù)量概念，是周長概念中量的本質(zhì)。

三、多維活動，層層辨析拓思維

在教學(xué)設(shè)計中，以任務(wù)驅(qū)動促進(jìn)學(xué)生探索，力圖讓學(xué)生的學(xué)習(xí)能觸及知識本質(zhì)，并設(shè)計實施具有挑戰(zhàn)性的活動任務(wù)，促進(jìn)學(xué)生對知識的深度理解。以下就教學(xué)流程列舉。

1.引入邊線，認(rèn)識一周

設(shè)計螞蟻運(yùn)動會的情境，讓學(xué)生找到樹葉的邊線。

對學(xué)生來說，邊線本身并不難理解。有了單元整體備課的視野，發(fā)現(xiàn)難的是在平面中找到邊線，學(xué)生容易受到面的干擾，忽略了邊線。所以，從二維圖形中剝離出一維的邊線，幫助學(xué)生消除面的干擾，從面中看到線才是難點，才是讓周長可視的意義。先讓學(xué)生找到并指出樹葉的邊線，建立對一周的初步感知。再描出樹葉的邊線，把樹葉拿開直視留在黑板上的邊線，就是要將二維圖形中的一維線段剝離出來，幫助學(xué)生排除面的干擾，引導(dǎo)學(xué)生發(fā)現(xiàn)這條邊線就是樹葉的一周，讓圖形的一周變得直觀可視[2]。

2.分析反思，感受一周

（1）師：樹葉有它的一周，身邊物體的表面有一周嗎？同桌互相找一找，指一指。讓學(xué)生從身邊熟悉的物體入手，明確一周存在于許多物體的表面，就在我們的身邊。也能在指一指的過程中再次感受它的邊線就是一周。

（2）師：物體表面有一周，圖形有一周嗎？你能描出下面圖形的一周嗎？

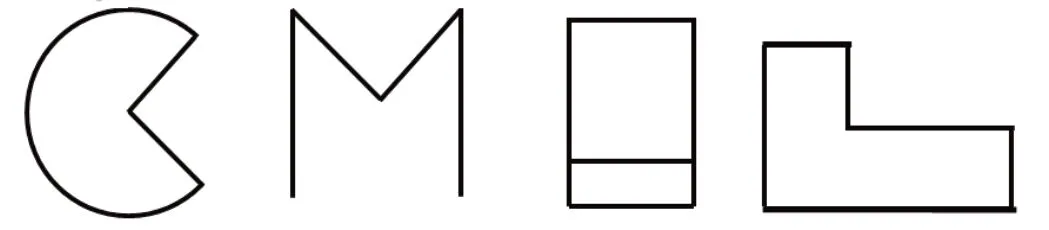
沒有了面的干擾后，也初步感受了“一周”后，我們再來聚焦問題：到底什么是一周？

學(xué)生描出一周后，及時發(fā)現(xiàn)學(xué)生典型錯例，引導(dǎo)學(xué)生分析、反思誰畫得對。隨后馬上追問：到底怎樣才是圖形的一周？學(xué)生再分陣營來擺事實講道理。學(xué)生在辨析、梳理、交流碰撞中，明確里面的線段不是圖形的邊線不是圖形的一周，逐步清晰地構(gòu)建周長中“周”的概念。

（3）聚焦M字形圖形，師：為什么都沒有描出一周？

學(xué)生從已經(jīng)從前面環(huán)節(jié)的辨析中積累對“一周”的感知，自然認(rèn)為此圖無法從起點開始繞一周后再回到起點，不是一個封閉圖形，當(dāng)然也就沒有一周了。又從“能把它變成一個封閉圖形嗎”這個變化中，再次加深學(xué)生對圖形一周的認(rèn)知。

3.動手操作，認(rèn)識周長

基于單元整體備課對知識本質(zhì)的分析。周長是通過度量得到的，度量物體表面或平面圖形邊線的長度，得到的這個結(jié)果就是它的周長，其本質(zhì)就是長度單位的累加。

（1）基于此設(shè)計“你如何知道上述第四幅圖形一周的長度”的問題。

生1：量出每一條邊的長度再加起來。

生2：用格子圖來測量。

生3：用繩子圍一圍，在量出繩子的長度。

利用格子圖測量就是為了突顯度量單位的累加這個核心。通過課件全班同學(xué)一起數(shù)一數(shù)，讓學(xué)生明確這些測量方法實際上都是把圖形的邊線數(shù)出來再加起來，這個圖形一周有幾個1厘米，它的一周就是幾厘米。這就指向了度量的本質(zhì)：長度單位的累加；也引出了周長的定義：封閉圖形一周的長度。

（2）師：一只螞蟻沿著樹葉一周跑，一只沿著正方形磚塊一周邊線跑，誰先跑完一周，誰就贏，如果你是螞蟻，你會選擇哪個圖形跑？

學(xué)生選擇哪個圖形？（跑道短的）就要意識到就是在比較周長的長短，建立描述周長不是用大小，而是用長短來比較的直觀感受。

生1：正方形用直尺量一條邊，算出4條邊的總和就是它的周長。

生2：用繩子繞樹葉一周，展開拉直后繩子的長度就是它的周長。

針對不同情況，學(xué)生要選擇合適測量工具：直邊可以直接用直尺測量（同時還可利用正方形的特征快速計算周長），曲邊圖形用線繞再測量線的長度，滲透化曲為直的數(shù)學(xué)思想。

4.辨析說理，深化概念

（1）快速判斷，下面兩個圖形的周長一樣嗎？

（2）長方形中加一筆，分成兩個周長一樣的圖形。

（3）拿走一個小方塊，周長會變嗎？

三個活動層層深入，讓學(xué)生在辯一辯、說一說中體會周長的本質(zhì)特征，學(xué)生的這種卷入式的學(xué)習(xí)狀態(tài)，就是在深度學(xué)習(xí)。筆者通過設(shè)計多維的活動，讓學(xué)生思維碰撞，在層層豐富的活動中探索圖形周長的“變與不變”，深化周長是一維長度的概念，不受面大小的影響，從而拓展學(xué)生的思維，同時促進(jìn)學(xué)生空間觀念、推理能力、創(chuàng)新意識的發(fā)展。

四、反思改進(jìn)，數(shù)據(jù)分析促發(fā)展

借助COP大數(shù)據(jù)的分析，引起了筆者的一些思考，比如：缺乏對學(xué)生問題意識的培養(yǎng)。筆者覺得可以在以下環(huán)節(jié)進(jìn)行調(diào)整：在描出圖形一周有不同的畫法時，基于學(xué)生的困惑，以“兩幅作品，你有什么疑問？”引導(dǎo)學(xué)生自己提出問題：誰畫得對？到底怎樣才是圖形的一周？學(xué)生再分陣營來擺事實講道理。這樣更能針對學(xué)生的難點、易混點和困惑點，呈現(xiàn)描出圖形一周的不同畫法，基于學(xué)生的典型錯例，通過層層反饋，引導(dǎo)學(xué)生學(xué)會提問、學(xué)會反思、學(xué)會辨析、學(xué)會表達(dá)、厘清思路，通過不同觀點的碰撞，逐步清晰地構(gòu)建“周長”的概念。再如COP數(shù)據(jù)分析中，學(xué)生討論后匯報的比例過低，體現(xiàn)在“加一筆，分成兩個周長一樣的圖形”環(huán)節(jié)時，只讓學(xué)生自己上臺說理，沒有關(guān)注臺下學(xué)生的反饋。其實，這個過程中學(xué)生易受面的影響，認(rèn)為圖形面越大，周長越長。所以，有必要讓學(xué)生充分討論AB兩個圖形周長是否一樣？通過分析、辨析、證明，最后匯報。這樣引導(dǎo)學(xué)生要關(guān)注圖形邊線的長度，深化了周長是一維長度的概念，從而拓展了學(xué)生的思維，促進(jìn)學(xué)生空間觀念的發(fā)展。

回顧周長一課的教學(xué)，筆者依靠單元整體備課的方法，能有效引導(dǎo)學(xué)生走向深度的學(xué)習(xí)中。整節(jié)課從備課思考到實踐探索，筆者始終以學(xué)生的立場為立足點，基于單元整體備課的框架，在課前對知識的內(nèi)在結(jié)構(gòu)做到逐層深化，然后對學(xué)生相關(guān)知識做了前測了解，再據(jù)此設(shè)計以問題鏈形式呈現(xiàn)的具有挑戰(zhàn)性的學(xué)習(xí)任務(wù)。在實施教學(xué)過程中，以多維活動為載體，設(shè)計針對學(xué)生困惑點、易混點、難點的問題情境，讓學(xué)生在體驗中去辨析、梳理、評價、提問，最終達(dá)到培養(yǎng)學(xué)生高階思維能力的目的。

總之，概念教學(xué)應(yīng)針對學(xué)生的難點、易混點和困惑點，基于學(xué)生的典型錯例，層層反饋，引導(dǎo)學(xué)生厘清思路、學(xué)會提問、學(xué)會辨析、學(xué)會表達(dá)、學(xué)會反思，通過不同觀點的碰撞，逐步清晰地構(gòu)建概念，拓展學(xué)生的思維，促進(jìn)學(xué)生空間觀念的發(fā)展。