基于Sobol’法的機床關鍵幾何誤差元素辨識方法研究

榮茂林，胡騰，何鄭曦，魏小建，吳昊榮

(1.西南石油大學機電工程學院，四川成都 610500；2.四川建筑職業技術學院，四川德陽 618000)

0 前言

數控機床受幾何誤差、熱誤差、裝配誤差等因素綜合影響，直接影響工件的加工精度。其中，幾何誤差具有穩定性高、重復性好、占比大、易于補償等特點，故誤差補償是提高機床加工性能最直接、經濟的方法。但機床誤差元素較多，空間誤差模型復雜，關鍵幾何誤差元素的篩選仍是誤差模型簡化中亟待解決的關鍵問題。

針對幾何誤差元素靈敏度分析問題，國內外學者進行了大量研究，使用的方法包括逐步回歸法、標準化回歸系數法和標準化秩相關系數法等。LI等以矩陣偏微分方程為基礎，根據五軸立式加工中心敏感性分析結果對機床進行改進，提高了機床加工精度。尹明和陳廷兵以局部靈敏度系數為基礎，提出一種新的全局靈敏度系數計算方法并應用于機床關鍵幾何誤差元素辨識。YAO等通過局部靈敏度分析，辨識出8項關鍵幾何誤差項，并通過實驗驗證了篩選結果的準確性。SOBOL提出了基于方差的全局靈敏度分析方法，辨識出機床的關鍵幾何誤差元素。上述方法通常只適用于對輸入與輸出呈線性相關的模型進行靈敏度分析，對于非線性復雜模型具有較大的局限性。

針對上述問題，以某三軸臥式加工中心為研究對象，提出了一套較完善的關鍵幾何誤差元素篩選方法技術體系。首先，分析機床運動鏈構成，以螺旋理論為基礎，建立包含21個誤差項的機床運動學模型(完備模型)；其次，使用Sobol’全局靈敏度分析法計算各誤差項對模型輸出的靈敏度值，從21個誤差項中篩選出關鍵幾何誤差元素；最后，利用所篩選的關鍵幾何誤差元素重新構建空間誤差模型(簡化模型)并與完備模型進行比較，驗證篩選結果的正確性。

1 臥式加工中心空間誤差模型

某臥式加工中心拓撲結構如圖1所示，機床坐標系固連于床身，原點為。記刀尖點和工件切削點在MCS下的初始位置分別為(、、)和(、、)。

圖1 機床拓撲結構

根據ISO230-7的定義，每個平動軸在空間中有6項誤差元素，分別是1項定位誤差、2項直線度誤差、3項角度誤差，即俯仰、偏擺和滾轉誤差，故三軸臥式加工中心有18項幾何誤差。除上述18項與位置相關的幾何誤差元素(Position-dependent Geometric Errors, PDGEs)外，3個平動軸還有3項與位置無關的幾何誤差元素(Position-independent Geometric Errors, PIGEs)，即軸與軸之間的垂直度誤差，故三軸機床共計21項幾何誤差元素，見表 1。

表1 三軸機床幾何誤差元素

機床的每一個名義運動都可以看做是機床在做剛體運動，誤差運動可看做機床剛體的微運動與微轉動。運動軸(=,,)的名義運動()與誤差運動()可根據螺旋理論表示為

(1)

(2)

垂直度的螺旋表達為

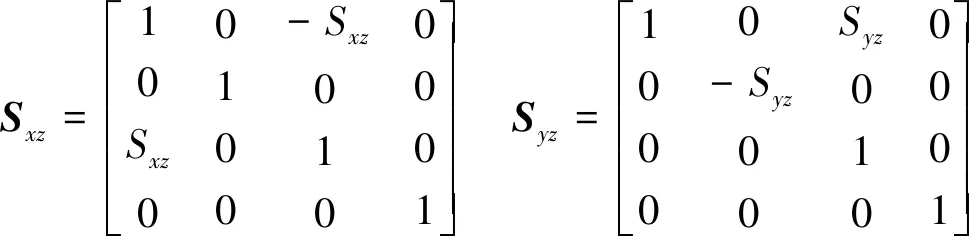
(3)

刀具鏈和工件鏈均在機床坐標系下表達，而空間誤差定義為刀尖點在工件坐標系下實際位置與理論位置之間的偏差，故需將工件鏈轉化為在工件坐標系下的表達，然后與刀具鏈進行耦合，從而得到機床整體運動鏈。由機床空間幾何誤差的螺旋表達形式可知，三軸臥式機床的空間誤差完備模型可由螺旋矩陣表示為

=((),(),())=(()·()···)·(()·()··()·()·)-

(()·)·(()·()·)=

(4)

2 Sobol’全局靈敏度分析方法

Sobol’全局靈敏度分析法基于方差分解而形成，其核心思想是對目標函數進行分解，利用各輸入量對應函數值的方差與模型總方差之比作為相應輸入量的靈敏度評價標準，通過方差之比可計算出各輸入量所對應的一階及高階靈敏度系數。其中一階靈敏度系數通常反映了某輸入量對模型輸出的單獨影響；高階靈敏度系數表示各輸入量之間的耦合作用對模型輸出的綜合影響。

針對空間誤差模型，假設目標函數為=()的形式，其中表示模型輸出,表示關于誤差元素的可積函數，=(,,…，)為維輸入參數。將目標函數根據Sobol方法分解為2項遞增階數之和的形式為

(5)

其中：為根據輸入量計算得到的目標函數模型的期望值，且當輸入確定時也隨之確定；表示第個誤差項所對應的函數值；表示第個與第個誤差項共同作用所對應的函數值。式中各子項之間滿足相互正交的關系，因此滿足如下關系

我院正常參考值范圍PTH為16～65 ng/L，血鈣為2.1～2.6 mmol/L，將甲狀旁腺素<16 ng/L定義為甲狀旁腺功能減退，血鈣<2.1 mmol/L且有伴發癥狀者診斷為低鈣血癥；術后6個月內PTH及血鈣恢復正常定義為暫時性甲狀旁腺功能減退；>6個月仍未恢復正常且需持續補鈣者定義為永久性甲狀旁腺功能減退。

(6)

其中：=1,2,…,。由此可得

=()

(7)

=-(|)-()

(8)

=-(|,)---()

(9)

其中:為第個輸入，-表示除以外的所有輸入，-表示除和以外的所有輸入。將模型輸入量看做連續隨機性變量并計算函數方差，可得輸入函數的總方差為

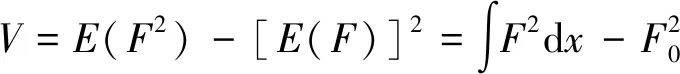
(10)

分別對單個誤差項和與其耦合的誤差項進行求方差可得

=()=[-(|)]

(11)

=()=[-(|,)]-

[-(|)]-[-(|)]

(12)

使用同樣的方法可以計算出其他高階項的方差。對式(5)進行求方差計算，可得到

(13)

基于方差的靈敏度分析定義為輸入量所對應方差與模型總方差的比值，故將式(13)的等號兩端同時除以函數總方差進行正交化，變換后可得

(14)

其中:

(15)

=={[-(|,)]-[-(|)]-[-(|)]}

(16)

為了衡量誤差項對空間誤差模型輸出量總方差的影響程度，將一階方差比值稱作誤差項 的一階敏感性系數，一階敏感性系數的大小直接反映該誤差項對模型輸出的影響程度大小。為了衡量誤差項與耦合后對模型輸出的影響程度，將二階方差比值稱為二階敏感性系數，值越大說明誤差項和之間的耦合作用越明顯。 其他高階項具有類似的含義。一般來說，誤差元素之間存在多元素相互耦合，且耦合效果不可忽略，為了能夠更加準確地描述誤差元素對模型輸出的總體影響，引入總體敏感系數。的計算方式為

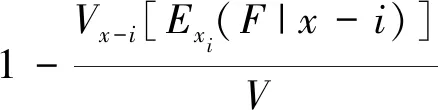
(17)

可簡單看作是的一階敏感性系數和所有與有耦合作用的高階敏感性系數之和。

3 蒙特卡洛估算

Sobol’全局靈敏度分析方法相較于傳統的蒙特卡洛采樣法具有更好的準確性與收斂性，其實質是使用低差異性序列的準蒙特卡洛方法。在進行靈敏度分析計算之前，需確定誤差項的變化范圍，然后使用Sobol’法根據元素范圍對誤差項進行準蒙特卡洛采樣，得到兩個誤差矩陣和，矩陣和矩陣相互獨立、互不影響。在此基礎上，以矩陣為矩陣的主體，利用矩陣的第列替換矩陣中的第列，其余項保持不變，得到矩陣()。()的產生過程如下

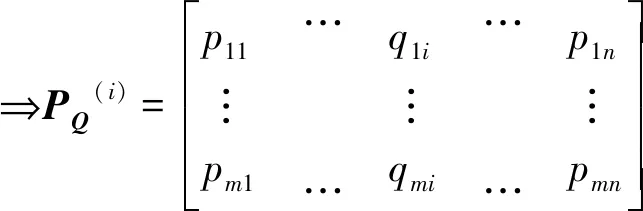
(18)

由公式(11)—(18)可知，一階靈敏度和總靈敏度的估算可分別表達為

(19)

(20)

4 模擬仿真

為探究三軸臥式加工中心幾何誤差元素對機床空間誤差的影響程度及簡化空間誤差模型，驗證所提關鍵誤差元素篩選方法的有效性，以圖1所示三軸臥式加工中心為研究對象，進行仿真計算。機床的工作空間為700 mm×600 mm×500 mm，根據機床空間誤差模型，其變量為21項幾何誤差元素，輸出為機床在刀尖點處空間誤差在、、方向的分量。依據數控機床出廠幾何精度檢驗標準可定義幾何誤差元素數值范圍。為提升機床精度、滿足設計需要，機床設計過程中需采用控制壓縮系數來保證機床設計精度，因此仿真時幾何誤差的取值為標準值的2倍。21項誤差服從均勻分布，-變化范圍如表 2所示。

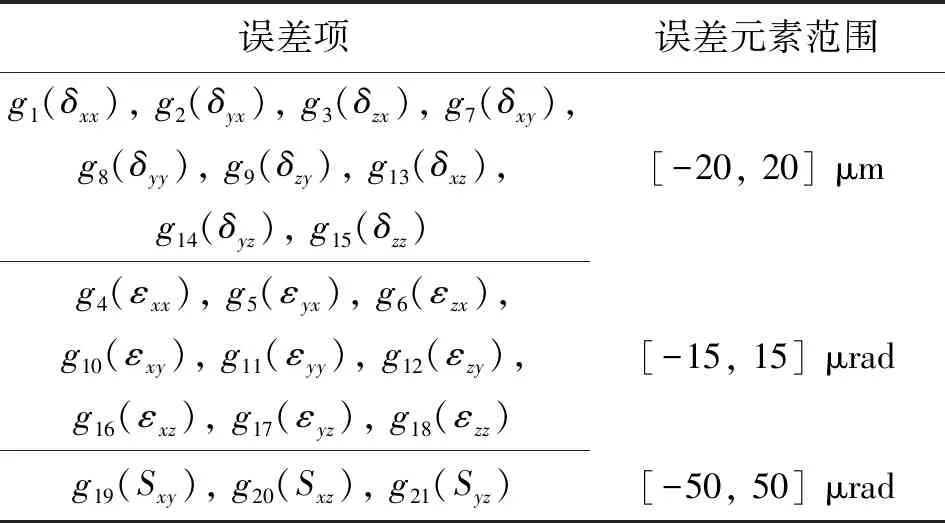
表2 機床幾何誤差元素范圍

利用Sobol’法基于低差異性序列的準蒙特卡洛法對輸入參數的空間域進行采樣，便于提高仿真計算的收斂性、穩定性以及準確性。根據誤差元素范圍對誤差元素進行抽樣，獲得誤差元素的Sobol低差異性序列，設定采樣的樣本量=10 000，采用Sobol’法對機床3個方向的空間誤差分量()、()、()進行分析，計算出各誤差元素分別對于()、()、()的一階靈敏度及總靈敏度，如圖 2—圖 4所示。

可以看出:各誤差元素對于空間誤差分量的影響程度不同。為了在保證模型預測精度的同時，又要盡可能篩選出關鍵幾何誤差元素，所以以靈敏度占比90%為界限，劃分關鍵幾何誤差元素與非關鍵幾何誤差元素。即將所計算的靈敏度值降序排列，靈敏度值大的幾項進行求和記為sum(1-)()，當sum(1-)()/sum()>0.9時，定義總靈敏度值大的前幾項為關鍵幾何誤差元素，結果如表3所示。

圖2 (x)E靈敏度分析結果

圖3 (y)E靈敏度分析結果

圖4 (z)E靈敏度分析結果

表3 關鍵幾何誤差元素

為了驗證關鍵幾何誤差元素篩選結果，利用關鍵幾何誤差元素重新建立空間誤差預測模型(簡化模型)。將上面使用的樣本中所有非關鍵幾何誤差元素值全部置零，通過簡化模型計算獲得機床刀尖點位置誤差分量，與完備模型預測值進行對比，如圖5—圖7所示。

圖5 (x)E預測對比分析

圖6 (y)E預測對比分析

圖7 (z)E預測對比分析

通過對比結果可以看出：完備模型誤差分量預測值的范圍為(-0.3，0.35)mm，簡化模型預測值與完備模型預測值的殘差為(-0.05,0.05)mm。不難看出，當不考慮非關鍵幾何誤差元素對模型的影響時，對模型的預測性能影響較小，簡化后的誤差預測模型仍保持較高準確度，元素簡化率為48%，殘差保持在20%以內，說明該方法能夠準確剔除機床空間誤差模型中非關鍵幾何誤差元素，保留關鍵幾何誤差元素。

5 結論

(1)分析了機床拓撲結構，運用螺旋理論建立了機床運動誤差模型。所有誤差元素均在機床坐標系下表述，無需建立繁雜的局部坐標系，簡化了建模過程，提高了建模效率。

(2)分析了Sobol’全局靈敏度分析方法的原理及靈敏度值的計算，解析了蒙特卡洛估計法的采樣矩陣生成方法。

(3)利用Sobol’全局靈敏度分析方法對機床空間誤差建模進行計算，通過仿真計算分析，從21項幾何誤差元素中篩選出12項關鍵幾何誤差元素，誤差元素項簡化率為48%；使用關鍵幾何誤差元素建立的機床空間誤差模型仍具有較高的預測準確性，殘差保持在±0.05 mm以內，說明作者所提出建模方法與關鍵幾何誤差元素篩選方法是準確、有效的，為空間誤差模型簡化、誤差元素辨識以及誤差補償提供理論支撐。