基于距離-角度多移動機器人編隊避障策略

咼生富，張鵬超，李海婷，徐鵬飛，劉亞恒

(1.陜西理工大學機械工程學院,陜西漢中 723000；2.陜西省工業自動化重點實驗室,陜西漢中 723000；3.陜西理工大學電氣工程學院,陜西漢中 723000)

0 前言

多移動機器人系統已廣泛應用于軍事及日常生活等場景，如人員搜救、合作搬運、無人機表演及機器人足球等。編隊控制與避障作為多移動機器人系統的關鍵問題，眾多學者對其進行了大量的研究。在多機器人合作完成任務過程中會遇到靜態或動態障礙物，所以有效避障是必要的，否則會造成任務失敗。

目前常用的避障方法分為兩種：一種是編隊拆分避障，如柵格法、可視圖法、模糊邏輯法、RTT算法、遺傳算法等；另一種為編隊整體避障，如人工勢場法、模型預測控制法、固定隊形變換法和基于行為法等。DAI等采用具有速度約束的多機器人規避和穿越障礙物的切換編隊策略，主要利用幾何避障控制方法來規劃安全路徑，但需要精確找到航路點才可以穩定隊形進行切換。陳剛等人公開一種基于模糊控制的以領航機器人廣播的形式告知所有跟隨機器人避障，跟隨者根據存儲的不同隊形信息以及領航機器人廣播的信息切換隊形，但模糊規則繁雜且屬人為規定，控制精度難以保證，且沒有考慮避障后隊形恢復和機器人之間在避障過程中碰撞問題。張佳龍等公開一種基于斥力場函數的編隊避障方法以及避障后路徑重規劃策略，保證在多機編隊執行任務中，實現機內實時避障，但斥力場越大，無人機離開觸發區的響應速度和運動速度越快，隊形變換超調量較大，控制系統穩定性降低。編隊整體避障需保持編隊內部隊形，通過動態調節隊形進行在線避障，相比于拆分避障，更具有靈活性、整體性和可靠性，可以有效避免拆分避障出現的跟隨者掉隊、機器人之間的碰撞問題。但多移動機機器人之間若沒有進行有效的協調和溝通，將不能發揮出多機協同避障的優勢，造成嚴重的經濟損失。因此，設計一種合理有效的編隊避障控制算法對多移動機器人系統的應用具有重要意義。

本文作者綜合考慮上述整體編隊避障過程中存在的系統響應慢、隊形變換超調量大、控制精度低和在避障過程中機器人相互間會發生碰撞的問題，提出一種距離-角度優先級的避障策略，通過建立隊形數據庫，根據障礙物類型的不同，選擇合理的避障隊形進行避障，順利通過障礙物后，快速恢復原隊形繼續完成任務。

1 領航-跟隨隊形結構模型及隊形數據庫的建立

1.1 領航-跟隨隊形結構模型

為減小跟隨者對領航者的過度依賴，避免鏈式結構造成的跟蹤誤差累積問題，采用虛擬領航-跟隨運動結構，如圖1所示。

圖1 跟隨者與領航者相對運動模型

設領航者的位姿為=[],=[]，跟隨機器人的位姿為=[],=[]，由圖1可得跟隨機器人與領航者的相對位姿方程：

(1)

其中:Δ=-,Δ=-，和為實際運動軌跡，和為理想運動軌跡。

由圖1得跟隨機器人的運動方程：

(2)

1.2 建立隊形數據庫

機器人的基本隊形主要有一字形、楔形、圓形和三角形等，如圖2所示。

圖2 隊形數據庫中的基本隊形形狀

在每個隊形中都至少有一個領航機器人，其余跟隨機器人接收領航者傳遞的消息，形成目標隊形。多機器人在執行任務過程中遇到障礙，通常是將隊形變化成一字形通過障礙物，不考慮機器人的運動特性、具體環境情況和障礙物的類型，這并非是最優的避障方法。圖3給出了兩種不同的隊形進行避障，其中圖3(a)中由原有隊形變成一字隊形，盡管該隊形容易通過當前障礙物，但在一定程度上增加了機器人避障路徑長度，收斂隊形的時間長，且易發生內部碰撞，隊形失真度比較大。而圖3(b)中以隊形內部角度縮小形成的隊形通過障礙物，編隊沒有改變整體隊形結構，只是在不會發生內部碰撞的條件下，對機器人編隊隊形進行收縮，收縮后的隊形順利通過障礙物，在當前場景下，圖3(b)中的避障方法明顯要優于圖3(a)。

圖3 不同隊形避障方式

以上是從具體的場景比較兩種不同隊形的優劣程度，在實際避障過程中，移動機器人整體如何自主地選擇適應當前環境約束條件的拓撲結構需提出相對應的避障策略。

目前缺少統一有效的方式來定義多移動機器人編隊的隊形形狀。為了方便描述編隊控制中具體領航者-跟隨者關系及隊形形狀信息。下面舉例說明：

設有3個機器人參與編隊，虛擬領航者表示為L，其位置坐標表示為[],跟隨者表示為F(=1,2,3)，常用隊形有一字形、三角形，如圖4、圖5所示。根據機器人數量設定相應的隊形數據庫。

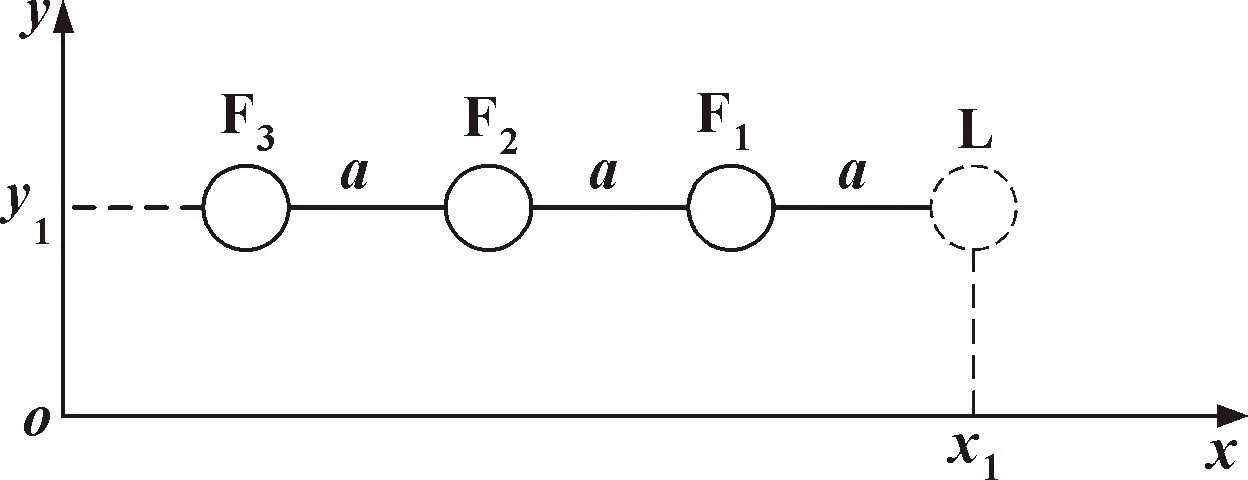
圖4 一字形編隊位置示意

圖5 三角形編隊位置示意

領航者與跟隨者坐標如表1和表2所示。

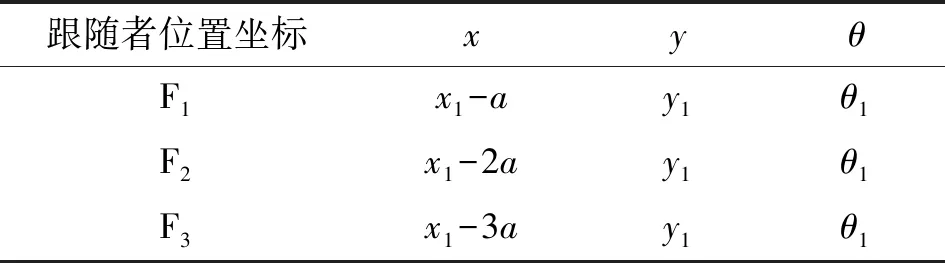
表1 一字形隊形各跟隨者位置坐標

表2 三角形隊形各跟隨者位置坐標

通過建立隊形數據庫，便于領航者迅速做出隊形選擇，降低計算復雜度，提高決策效率。

2 距離-角度優先級避障策略

充分考慮在隊形變換過程中的環境約束，合理選擇隊形避障方式，分別針對單側障礙物和雙側障礙物提出基于距離-角度優先級的隊形變化避障策略。

圖6所示為多移動機器人避障算法流程。機器人編隊在向目標點運動的過程中，領航機器人通過自身攜帶的傳感器感知周圍環境信息，得到領航機器人與障礙物之間的相對位置，并考慮各個機器人的自身安全距離和通信范圍的關系判斷當前以何種隊形避障最優；跟隨者根據領航者的指令進行避障。

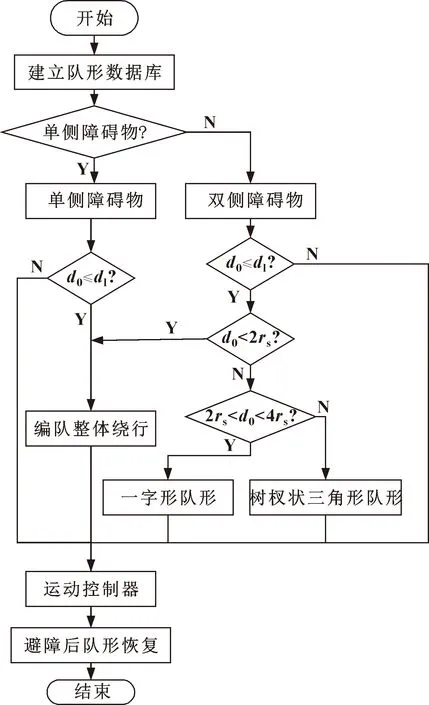
圖6 多移動機器人避障流程

2.1 單雙側障礙物避障策略

設機器人自身安全距離為半徑為，則兩個機器人并排運動的最小安全距離為4，3個機器人跟隨領航者以三角形隊形沿水平方向運動。

(1)單側障礙物避障策略

單側障礙物避障示意如圖7—圖8所示。

圖7 躲避上側障礙物示意

圖8 躲避下側障礙物示意

編隊遇到單側障礙物時，如圖7所示，通過比較障礙物與編隊的距離和sin+的大小，判斷編隊是否需要避障；若>sin+，則不需要避障。若≤sin+，則需避障，同時機器人通過傳感器判斷障礙物，位于前進方向的上側或下側，若為上側，則機器人系統保持初始隊形右拐進行避障，若為下側，則機器人系統保持初始隊形左拐前進進行避障；當編隊整體通過障礙物后隊形收斂到原軌跡水平線繼續前行。

(2)雙側障礙物避障策略

當領航機器人檢測到雙側障礙物時，如圖9所示，如果>，編隊中的成員機器人保持現有隊形形狀即可通過障礙物。若≤，編隊無法直接通過障礙物區域，需要將隊形切換到另一種狀態，保障編隊順利通過。其中=2sin+2。

雙側障礙物屬于復雜區域，整體編隊需要具體判斷以哪種隊形避障，若<2，則按單側避障方案繞行避障；若2<<4，需變為一字隊形通過障礙物；若>4時，編隊通過減小角度減小隊形的寬度，依然按照原隊形即可通過障礙物。其中表示障礙物之間的最小間距。

圖9 樹杈狀三角形隊形避障示意

通過分析對一般環境中可能出現的單雙側障礙物，考慮機器人自身安全距離及隊形整體與障礙物之間距離，提出距離-角度優先級避障策略，即先判斷是否需要避障，其次優先考慮距離判斷是否需要改變隊形，最后決定是否需要改變角度選擇合適隊形通過障礙物。當編隊中最后一個機器人成功通過障礙物后，由領航者機器人發布隊形恢復指令，隊形中的跟隨機器人以各自領航者為參考恢復隊形。

2.2 隊形快速恢復算法

為提高多機器人的工作效率，當機器人編隊整體通過障礙物后需及時恢復隊形，沿原軌跡繼續前行，設避障后領航者位姿為()=[]，設隊形快速恢復函數為

()=(-)e-+

(3)

其中：>0；為初始值即避障后虛擬領航者位置狀態量；為()的穩態值即恢復隊形后的位置狀態量。()按指數快速遞減到，可實現隊形以指數形式快速恢復。

3 仿真實驗及結果分析

為了充分驗證文中避障策略的可行性和優越性，在兩種不同的障礙物環境中進行仿真。

將3個機器人的初始編隊設置為三角形，初始位置分別為=[2 1 0 0]、=[0 1 1 0]、=[0 9 0],理想線速度、角速度分別為=1 m/s、=0.5 rad/s，機器人自身安全距離為0.3 m，最大通信距離為5 m，最大通信角度為120°，仿真結果如圖10—圖13所示。

圖10 躲避單側障礙物

圖11 躲避雙側障礙物

圖12 躲避雙側障礙物時實際與理想位置跟蹤誤差

圖13 躲避雙側障礙物時實際與理想速度跟蹤誤差

圖10、圖11分別為在單、雙側障礙物環境中機器人群的避障及隊形恢復示意，可得：機器人以三角形隊形運動遇到單側障礙物時，能夠準確判別出障礙物的方向并控制編隊轉向安全通過障礙物；遇到雙側障礙物時，充分考慮障礙物與隊形的間距和角度，開始縮小隊形通過第一個障礙物，然后變為一字形隊形通過第二個障礙物，并在完全通過障礙物時迅速在3 s內恢復隊形繼續前進。

圖12為機器人躲避雙側障礙物過程中的位置跟蹤誤差曲線，當機器人保持隊形運動時，在軸方向上的平均絕對誤差為0.001 1 m，在軸方向上的平均絕對誤差為0.001 5 m，角度跟蹤平均絕對誤差為0.001 2 rad。當機器人變換隊形時，在=30 s時隊形超調量最大，在軸上最大超調量為3 m，軸上的為2 m，即隊形最大超調距離約為3.606 m<5 m,角度最大超調量為1.2 rad<2π/3，機器人群始終處于通信范圍內，沒有出現掉隊和碰撞現象。圖13為機器人躲避雙側障礙物過程中的速度跟蹤誤差：當機器人保持隊形運動時，線速度跟蹤平均絕對誤差為0.001 2 m/s，角速度跟蹤平均絕對誤差為0.001 1 rad/s；當機器人變換隊形時，考慮到實際情況，轉彎時需要減小速度，所以線速度與角速度跟蹤均出現了超調，但避障后，能夠在5 s內恢復原有速度繼續前進。

為了進一步說明該避障策略的高效性，與文獻[12]中提出的幾何避障控制算法作對比，設置的障礙物和初始隊形與圖11中保持一致，仿真結果見圖14—圖16。

圖14是文獻[12]避障策略仿真軌跡，編隊在進行隊形變換時，軌跡不平滑，導致隊形超調量較大。圖15為文獻[12]中避障策略下機器人躲避雙側障礙物過程中的位置跟蹤誤差曲線，當機器人變換隊形時，在=30 s時隊形超調量最大，軸方向最大超調量為3.4 m，軸上為2.2 m，即隊形超調最大距離為4.04 m。圖16為文獻[12]中避障策略下機器人躲避雙側障礙物過程中的速度跟蹤誤差，當機器人變換隊形時，完成避障后編隊需要7 s才能恢復初始隊形。

圖14 文獻[12]中避障策略雙側避障

圖15 文獻[12]中避障策略與理想位置跟蹤誤差

圖16 文獻[12]中避障策略與理想速度跟蹤誤差

為方便表述，將文中所提避障策略、文獻[12]中設計的避障方法分別表述為A算法和B算法。由圖11和圖14可得：與B算法相比，A算法下編隊軌跡相對比較平滑；由圖12、13和圖15、16可知：當機器人保持隊形運動時，與B算法相比，A算法下位置跟蹤誤差在軸方向上的平均絕對誤差、在軸方向上的平均絕對誤差以及角度跟蹤平均絕對誤差分別提高了0.003 m和0.004 m；在線速度和角速度跟蹤方面，A算法比B算法分別提高了0.002 m/s和0.004 rad/s；此外，隊形恢復時間縮短了28.57%。

以上是對編隊避障過程中的跟蹤誤差進行具體對比分析，證明了A算法的有效性。為了進一步說明A算法完成避障的高效性，現對編隊整體避障過程進行綜合評價，評價指標函數設計如下：

(1)避障路徑函數

當機器人速度一定時，編隊是否能夠高效完成任務取決于路徑的長短。將走過路徑的長短作為評價避障性能函數之一，來描述機器人群避障走過路徑的長度。避障路徑函數為

(4)

其中：表示編隊開始避障的初始時刻；表示編隊完全通過障礙物的時刻。函數值與避障效率成反比。

(2)隊形結構失真函數

切換隊形時會引起編隊控制系統不穩定，需要編隊隊形變形量盡可能地小。將隊形結構失真作為評價避障性能的函數之一，來描述隊形變換與原始隊形結構畸變程度。隊形結構失真函數為

(5)

其中：表示編隊中機器人數量；()表示機器人在性切換隊形中位置；(0)表示機器人在初始隊形中的位置；，lF為各跟隨者與領航者的相對距離。函數值表明隊形失真度，值越大系統越不穩定，隊形難以恢復。

(3)隊形恢復時間

當機器人通過障礙物時，需要恢復隊形繼續前行完成任務，因此，隊形恢復效率也是影響編隊整體執行任務效率的影響因素之一。將隊形恢復時間作為評價避障的附加技術指標，一方面來描述避障時隊形的分散程度，另一方面，編隊過程中需要多次變換隊形時，就需要多次恢復隊形，隊形恢復時間從側面反映出避障的效率。隊形恢復時間函數為

(6)

其中：表示編隊切換隊形的次數；s表示避障后開始恢復隊形的時刻；d表示隊形恢復結束的時刻。函數值與避障效率成反比。

由表3可得：比B算法相比，路徑的長度方面，A算法下的避障路徑更短，減少了14.29%；在隊形結構畸變程度方面，A算法減小了12.5%；在隊形恢復時間上，A算法縮短了28.57%，極大地提高了避障效率。綜上，文中編隊避障策略效果更佳。

表3 文中方法與文獻[12]中方法的指標評價對比

4 結論

針對復雜環境下多移動機器人編隊整體避障效率低的問題，提出一種基于距離-角度優先級避障策略。該策略通過領航者機器人攜帶的傳感器獲取未知環境中障礙物的具體信息，引導整體編隊通過障礙區。相對于傳統的隊形避障方法，此方法充分考慮編隊避障中環境、自身安全和通信范圍的約束，先通過整體編隊隊形的寬度與障礙物可通過區域的比較，選擇合適隊形，然后各跟隨者調整自己與領航者的角度，形成目標隊形通過障礙物。該策略充分考慮了當前環境對隊形的影響，具有使編隊自主切換到當前避障合理隊形的良好性能，對于多移動機器人編隊避障研究具有一定的理論意義和參考價值。