機器人柔性掃描測量系統標定方法*
王鈺鑫,周志龍,劉 巍
(大連理工大學 機械工程學院,遼寧 大連 116024)
隨著制造業水平的不斷發展,廣泛涌現出一些大尺寸復雜曲面零件[1-3]。這些零件具有測量尺寸大、型面復雜、難以移動等特點,因此難以采用三坐標測量機等方式進行接觸式測量。與坐標測量機相比,以結構光視覺測量為代表的非接觸式測量得到了廣泛的應用[4-6]。將結構光掃描儀集成到機器人系統中即可構成柔性測量系統。該系統兼顧了結構光掃描儀精度高、效率高和機器人柔性好、可適用于不同工作場景的特點。為了實現測量結果從掃描儀坐標系到機器人基坐標系的統一高精轉換,必須進行考慮到機械臂運動學誤差的手眼關系標定[7]。
傳統的手眼標定方法可以轉化為對AX=XB這個方程的求解問題。Tsai[8]通過機器人變換不同位姿對標定物進行拍攝,將手眼矩陣拆為平移部分和旋轉部分,再依次進行求解。Horaud[9]對此方程給出了一種基于四元數的求解方法。Zhuang[10]將相機和機器人作為整體進行一次性標定,從而求解出手眼標定參數。Ma[11]通過機器人做特定運動從而建立約束并進行求解。這些求解方式的共同特點是需要機器人做一些特定運動,將機器人作為標定精度鏈中的一環。但是,由于在制造裝配時存在誤差,工業機器人的理論運動學模型和實際運動學模型間存在偏差,因此這些方法會引入機器人的運動學參數誤差,進而影響到手眼標定的準確性。
本文提出了一種基于機器人與結構光掃描儀的柔性測量系統標定方法。首先通過機器人單軸旋轉以及基于羅德里格矩陣的算法進行手眼標定,獲得手眼關系矩陣;然后機器人變換不同位姿,測量特征點,基于距離約束對手眼關系參數和機器人運動學參數進行進一步標定;最后通過測量距離誤差來驗證標定結果的準確性。
1 測量原理
柔性測量系統由工業機器人和結構光掃描儀組成(見圖1),結構光掃描儀通過夾具安裝在機器人末端。測量時通過機器人變換不同位姿,掃描儀對被測特征進行拍攝,并將測量結果從掃描儀坐標系轉換到機器人基坐標系。柔性測量系統的主要坐標系包括機器人基坐標系Ob-XbYbZb、機器人末端坐標系Of-XfYfZf、掃描儀坐標系Os-XsYsZs和掃描儀夾具坐標系Oc-XcYcZc。則可得到特征點在機器人基坐標系下的坐標表示為:
(1)
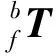
2 系統標定
2.1 機器人運動學模型
本文選用的機器人為六自由度工業機器人,采用目前最廣泛的DH模型對機器人進行運動學建模,即通過連桿長度ai、連桿轉角αi、連桿偏距di和關節轉角θi這4個參數求出相鄰連桿坐標系間的轉換矩陣[12]:
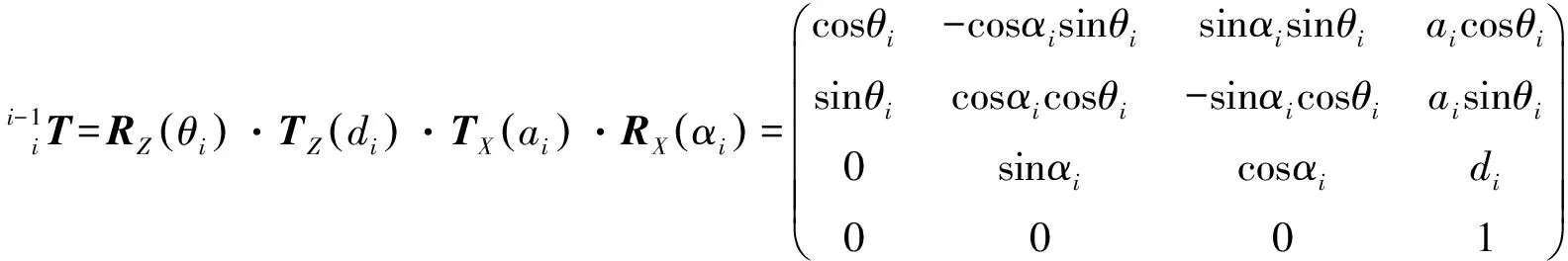
(2)
式中,TZ(di)、TX(ai)為平移矩陣;RZ(θi)、RX(αi)為旋轉矩陣。慮及相鄰關節軸線平行或接近平行產生的奇異性問題,引入繞Y軸旋轉的轉角β,建立機器人MDH模型[13],則相鄰連桿坐標系間的轉換矩陣為:
(3)
式中,cθi表示cosθi;sθi表示sinθi;依次類推。當相鄰軸不平行時,轉角β取零;當相鄰軸平行時,連桿偏距d取零。
2.2 手眼關系初步標定
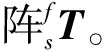
(4)
(5)
(6)
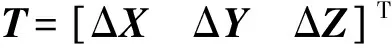
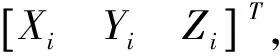
(7)
要求解此方程,首先需要得到特征點的重心化坐標,即將特征點原點的坐標轉換為特征點的重心坐標,計算式如下:
(8)
將式8代入式7可得:
(9)
對式9兩端取2-范數,因為λ>0且R為正交矩陣,因此可得:
(10)
對λ進行最小二乘估計,即可解出λ:
(11)
接下來求解R。引入一個反對稱矩陣:
(12)
式中,S包含a、b、c三個羅德里格參數。由羅德里格矩陣的性質可知:
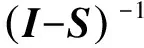
(13)
式中,I為三階單位矩陣。將式13代入式9,整理后得:
(14)
由間接平差模型可得:
(15)

由最小二乘估計,可得:
X=(BTB)-1BTl
(16)
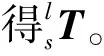
2.3 手眼關系誤差與機器人運動學參數誤差聯合標定
為了提高測量系統的測量精度,考慮到手眼關系參數誤差和機器人運動學參數誤差,提出了一種基于距離約束的標定方法,進一步修正手眼關系參數和機器人運動學參數。即以兩特征點之間精確的已知距離作為校準目標,通過對特征點距離進行測量以求解機器人運動學參數誤差和手眼關系參數誤差[16]。
特征點在機器人基坐標系下的理論測量結果可表示為:
(17)
由于手眼關系參數和機器人運動學參數存在誤差,特征點的實際測量結果與理論測量結果有所差距,慮及測量誤差的實際測量結果可以表示為:
(18)
(19)
由微分運動學可得手眼關系誤差:
(20)
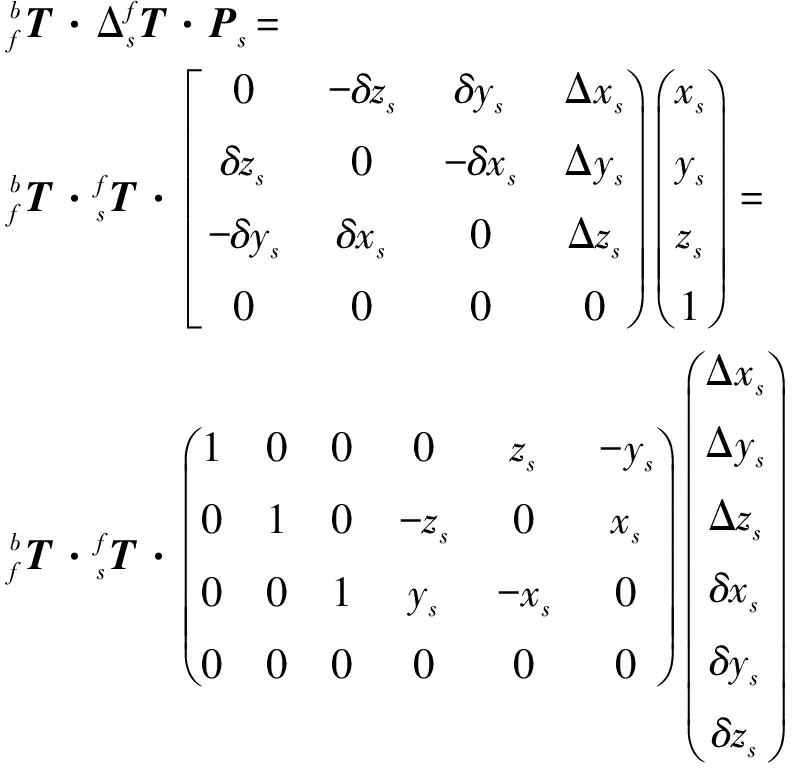
(21)
同理,由微分運動學可得機器人位姿誤差:
(22)

(23)
因需要求出機器人運動學參數誤差,故需建立出機器人末端位姿誤差和運動學參數誤差之間的關系。由式3可知,受機器人運動學參數誤差影響下的相鄰連桿坐標系間的轉換矩陣為:
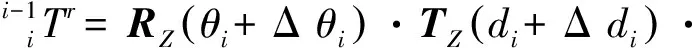
(24)
由微分運動學可得轉換矩陣誤差:
(25)
(26)
(27)
則有:
(28)
對比式26和式28可得:
(29)

(30)
式中,Gi為誤差系數矩陣;ΔEi為連桿i的參數誤差導致的連桿i末端誤差,需要將各個連桿的誤差轉換到機器人末端。設連桿坐標系{i}到機器人末端坐標系的轉換矩陣為:
(31)
則連桿坐標系{i}到機器人末端坐標系的雅可比矩陣為:
(32)
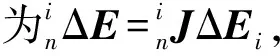
(33)
式中,ΔP= [Δθ1…Δθ6,Δd1…Δd6, Δa1…Δa6,Δα1…Δα6,Δβ2],共24個運動學參數誤差。代入式23得:
(34)
式34與式19、式21聯立,可得:
(35)
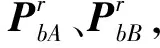
(36)
距離誤差可表示為:
(37)
將式36代入式37,得:
(38)
由于ΔK包含30個未知參數,因此需要機器人對至少30組特征點間的距離進行測量,進而建立具有30個以上式38的方程組,對該方程組進行求解,即可得到所求參數。
由于Q矩陣不滿秩,因此無法采用最小二乘法對此方程組進行求解。在這里采用Levenberg-Marquardt算法進行求解[18]。Levenberg-Marquardt算法的具體流程如下。
步驟1:設置權系數μ(一般取0.001)、初始點ΔK0和容許誤差ΔLmax。
步驟2:由參數誤差ΔKi求出距離測量值Li和系數矩陣Qi,其中i為迭代次數。
步驟3:由距離實際值Lr和距離測量值Li做差,得到距離誤差ΔLi。
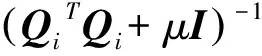
步驟5:若ΔLi+1<ΔLmax,則輸出ΔKi,結束流程;若ΔLi+1<ΔLi,則令ΔKi+1=ΔKi,μ=10μ,轉步驟4;否則,令μ=μ/10,轉步驟2。
3 試驗結果與分析
3.1 試驗系統
試驗現場的測量系統如圖4所示,機器人型號為KUKA KR10 R1420,最大工作范圍為1 420 mm,重復定位精度為0.04 mm;激光跟蹤儀型號為Leica AT960MR,測量精度為±15 μm+6 μm/m;掃描儀型號為Gocator 3506,測量精度為±12 μm。掃描儀通過夾具安裝在機器人末端,同時在掃描儀夾具上安裝靶球,以便激光跟蹤儀進行測量。
3.2 試驗過程
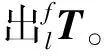
(39)
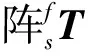
(40)
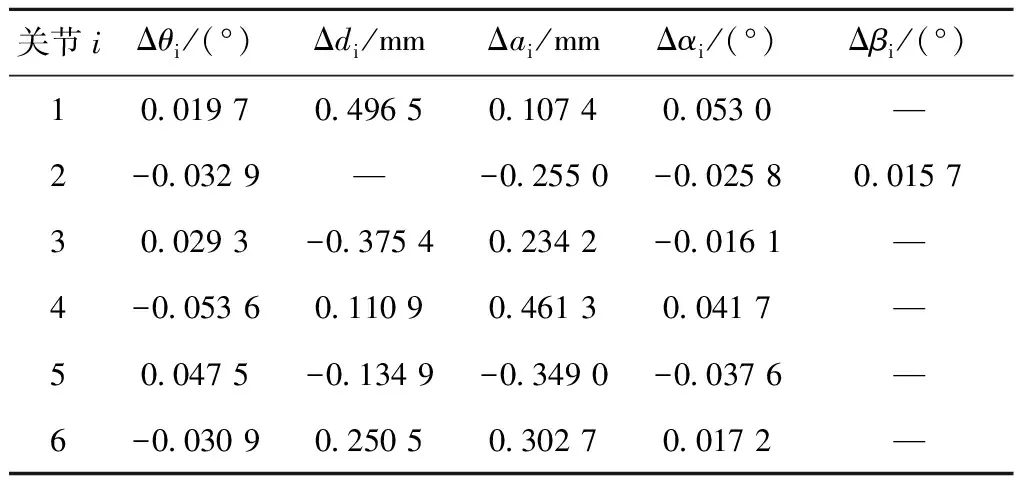
表1 機器人運動學參數誤差
3.3 試驗結果
修正參數后,重新計算特征點間的距離誤差,修正前后每組特征點距離誤差如圖6所示,距離誤差的最大值由0.870 0 mm減小到0.404 2 mm,平均值由0.661 4 mm減小到0.300 6 mm,驗證了該標定方法的有效性。
為了驗證機器人在全部工作空間內的標定精度,將靶尺在機器人的工作空間內均勻移動10個位置,對這10個位置的特征點距離進行測量,測量得到的標定前后每組特征點距離誤差如圖7所示,距離誤差的最大值由0.889 3 mm減小到0.424 9 mm,平均值由0.778 4 mm減小到0.385 2 mm,可見對柔性系統進行標定在機器人的全部工作空間內均有效。
4 結語
本文針對柔性測量系統整體測量精度不足問題,提出了一種基于距離約束的手眼關系參數和機器人運動學參數聯合標定方法。首先,通過機器人單軸旋轉與基于羅德里格矩陣的算法實現手眼關系初始標定,然后,基于距離約束實現對手眼關系參數誤差和機器人運動學參數誤差的辨識及修正,并通過試驗,驗證了標定精度。試驗結果表明,在機器人的工作空間內,距離誤差的最大值由0.889 3 mm降低到0.424 9 mm,平均值由0.778 4 mm降低到0.385 2 mm,驗證了該測量系統具有較高的測量精度。

