3-PRS & 3P混聯機構運動學分析

全紅鵬，林光春，黃金月，梁建波，王韜略，廖勛寶

(1.四川大學機械工程學院，四川成都 610065；2.四川阿斯特醫療器械有限公司技術部，四川瀘州646100)

0 前言

混聯機構兼具串聯機構和并聯機構的優點，具有承載能力強、剛度好、精度高、響應快、工作范圍大等優點，已被廣泛用于航天、醫療、工業、軍事等各個領域，具有良好的實用性能。

為了更好地運用混聯機構，國內外許多學者對其進行了研究。黃俊杰等提出用D-H法和圖形可視化相結合的方法對3-PRS并聯機構進行正向運動學求解。史曉娟和王高洋將仿真逆解曲線以樣條驅動函數形式輸入給3-UPU并聯機構,得出樣條驅動函數下的位置正解曲線。張偉中等設計了一種新型四自由度并聯機構，并采用螺旋理論分析了機構的運動特性。崔馬茹等采用空間封閉矢量法求解3-URPR并聯機構的位置逆解。康件麗等充分利用蒙特卡洛方法的隨機性，可以找到3-PRS并聯機構的所有位置正解。黃思等人采用雙參數數值延拓同倫算法求出正運動學的數值解。黃俊杰和趙俊偉運用遺傳算法并結合運動方程給出并聯機構運動學位置正解適應度函數和目標函數，將計算結果代入運動方程求出桿長。黃亮等人針對一種3SPS-3SRR并聯機構,運用符號法對該機構進行位置分析。楊應洪和尹顯明通過支鏈變異法,提出一種可滿足機床2R1T運動要求的2RPS-RPU并聯機構，并對其進行了運動學分析。

本文作者提出了一種新型3-PRS & 3P混聯機構，對混聯機構進行自由度分析；然后對該混聯機構進行機構運動學逆解和正解分析，再通過數值算例進行驗證；最后討論了該混聯機構動平臺2的運動范圍。通過以上分析，可以為后面分析該混聯機構的動力學及其運動控制提供了一定的理論基礎。

1 機構描述以及動、靜坐標系的建立

3-PRS & 3P混聯機構主要由定平臺、動平臺1、動平臺2、滑塊1、滑塊2、滑塊3、支鏈1、支鏈2、支鏈3、支鏈4、支鏈5、支鏈6組成，如圖1所示。其中定平臺與動平臺1通過3個移動副連接，動平臺1與3個滑塊通過3個移動副連接，滑塊1、滑塊2、滑塊3分別與支鏈4、支鏈5、支鏈6通過3個轉動副連接，支鏈4、支鏈5、支鏈6與動平臺2通過3個球副連接。各鉸接點分別為：(=1,2,3)、(=1,2,3)、(=1,2,3) 、(=1,2,3) ，如圖1所示。且、、構成一個邊長為的正三角形；、、構成一個邊長為的正三角形；、、構成一個邊長為的正三角形；、、構成一個邊長為的正三角形。

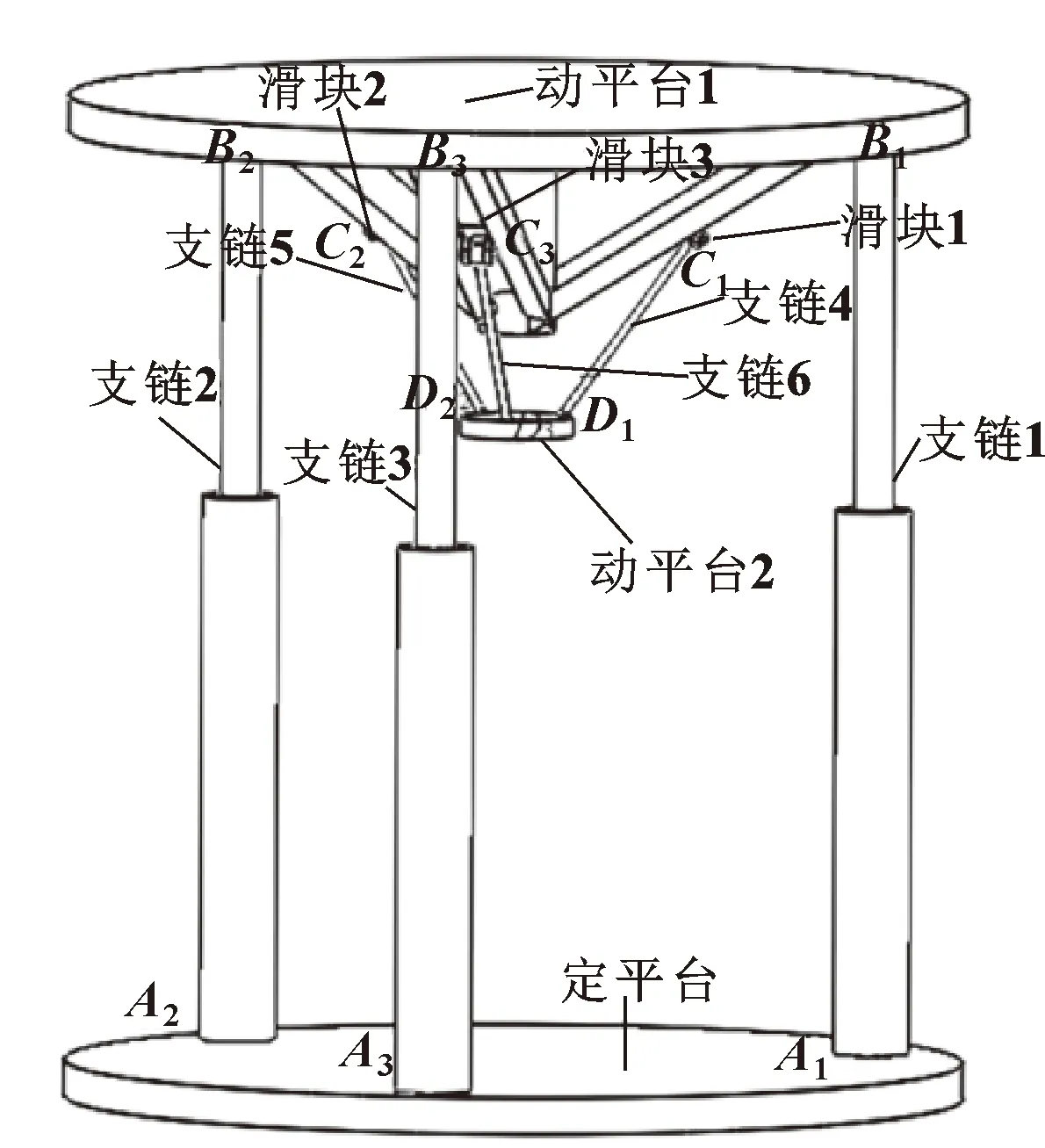
圖1 3-PRS & 3P混聯機構構型

為3-PRS & 3P混聯機構建立動、靜坐標系，如圖2所示，其中定平臺坐標系為-，動平臺1的坐標系為′-′′′，動平臺2的坐標系為″-″″″。(=1,2,3)在定坐標系下的方向高度為，(=1,2,3)在定坐標系下的方向高度為，(=1,2,3)在定坐標系下的方向高度為。

圖2 動、靜坐標系的建立

各鉸接點在定平臺坐標系-(初始位型)的坐標為

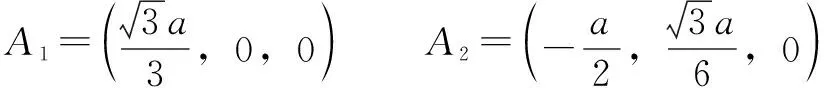
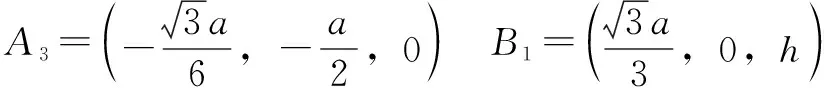
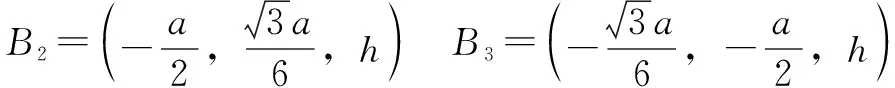
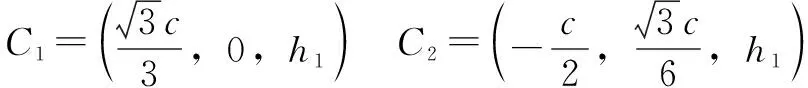
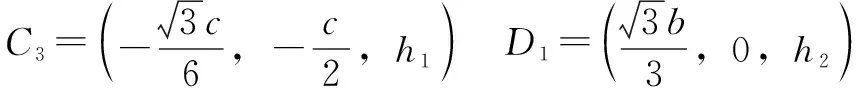
2 機構自由度分析

如圖2所示，各支鏈的運動螺旋系均在定平臺坐標系-下表示。支鏈1的運動螺旋系為

=(0 0 0; 0 0 1)

(1)

對支鏈1求反螺旋，得到支鏈1的約束螺旋系為

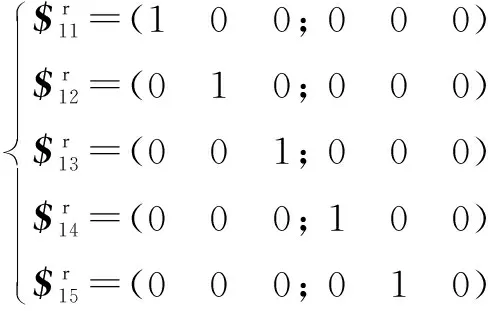
(2)

對式(2)求二次反螺旋得

(3)

同理支鏈2和支鏈3的運動螺旋系與支鏈1的運動螺旋系是一樣的，所以支鏈2和支鏈3的約束螺旋系與支鏈1的也一樣。所以動平臺1受到5個約束，分別約束繞著軸、軸、軸的轉動和沿著軸和軸的移動。所以動平臺1只有一個沿著軸的移動自由度。

支鏈4的運動螺旋系為

(4)

式中:、、、為非零的有限實數。對支鏈4求反螺旋，得到支鏈4的約束螺旋為

(5)

式(5)表示過點且平行支鏈4轉動副軸線的約束力。

由于機構具有對稱性，同理得支鏈5的約束反螺旋為

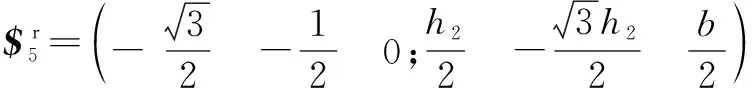
(6)

式(6)表示過點且平行支鏈5轉動副軸線的約束力。

同理支鏈6的約束反螺旋為

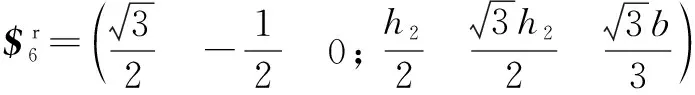
(7)

式(7)表示過點且平行支鏈6轉動副軸線的約束力。

對式(5)(6)(7)求二次反螺旋得：

(8)

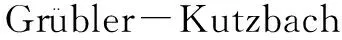
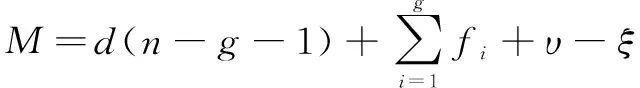
(9)

其中:表示機構的自由度;表示機構的階數，它依賴于公共約束，=6-;表示機構的構件數(包括固定構件);表示運動副數目;表示第個運動副的自由度;表示冗余約束;表示局部自由度。在該混聯機構中=6、=9，運動副所含有的自由度為18(3+3+3+2×3)，冗余約束=10，局部自由度=0。所以機構的自由度為：=6(9-12-1)+18+10-0=4。這與螺旋理論算出來的自由度一致。

3 機構運動學分析

由于支鏈1、支鏈2、支鏈3只改變動平臺1的工作空間，因此這里運動學分析時，先假設它們固定不動，而只考慮支鏈4、支鏈5、支鏈6運動的情況，這樣就簡化了分析的難度，相當于分析3-PRS并聯機構。后文再說明考慮了支鏈1、支鏈2、支鏈3運動時的情況。

3.1 機構的逆解分析

混聯機構逆解分析就是已知動平臺2中心″的位姿，求驅動桿長()(=1,2,3)的輸入量。設為球副所在平面的中心，繞著軸的轉角為，繞著軸的轉角為。

設動平臺2中心″在定平臺上的坐標=(,,)，(=1,2,3)在動平臺2的動坐標系下的坐標為(″,″,″)，則在定坐標系下的坐標表達式為·+(=1,2,3)。其中：

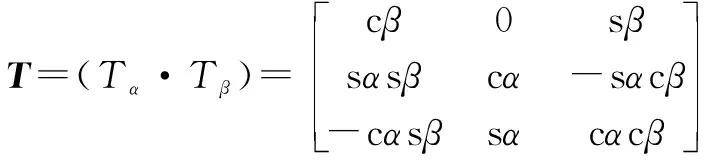
(10)

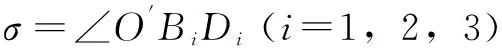
圖3 逆解分析模型

(11)

(=1,2,3)有兩組解，為了提高混聯機構的剛度，統一取負號，即點從頂部向底部滑動。

3.2 機構的正解分析

已知輸入桿長(=1,2,3)，求動平臺2的位姿。求解混聯機構的正解是有一定難度，而一般構型采用數值分析法進行求解。本文作者也采用數值分析法求解。已知移動驅動桿長的變化規律，則可以求出點的具體數值。點坐標表達式為:·+(=1,2,3)，這樣點坐標就含有未知參數、和。由于||=(=1,2,3)，則有

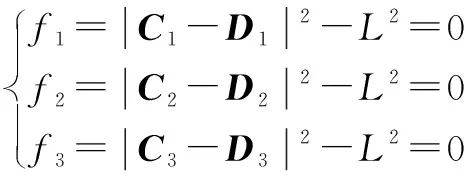
(12)

對式(12)，采用牛頓迭代法來求解該非線性方程組。其中，式(12)可以寫成

()=0，=(,,)，=(,,)。根據牛頓迭代法有：+1=-·，其中為雅可比矩陣：

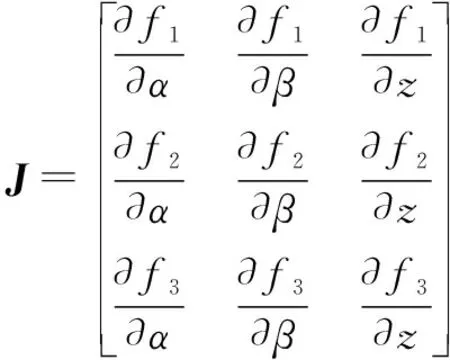
給定輸入參數1、2、3，根據給定的初始向量進行迭代，最后得到符合精度要求的向量，即混聯機構輸出位姿參數。初始向量的給定要符合機構的近似解，不然在一定的精度要求下，可能得不到解。

4 數值實例驗證及其仿真

下面通過表1所示的混聯機構具體的結構參數，對機構運動學的逆解模型和正解模型進行仿真和驗證。

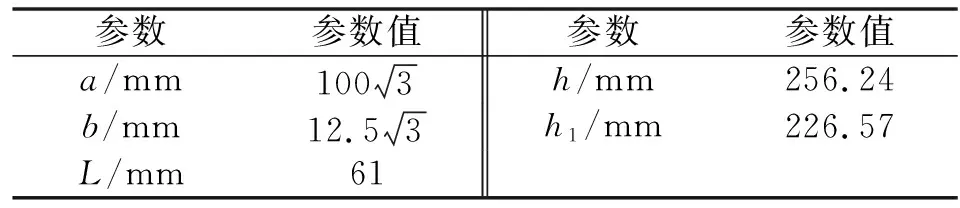
表1 具體的結構參數

其中:表示、、形成的正三角形邊長;表示動平臺2三個球副中心點形成的正三角形邊長;表示點(=1,2,3)到點(=1,2,3)的固定距離;表示點在定坐標系下的初始高度；表示點在定坐標系下的初始高度。

4.1 反解模型

給定動平臺2中心點″的運動規律如下：

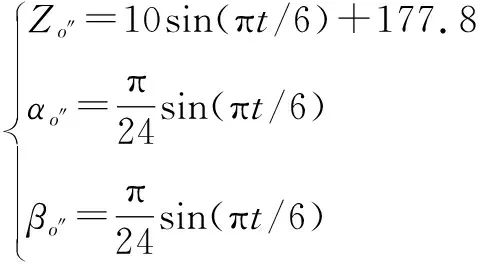
(13)

在SolidWorks中建立混聯機構三維模型，然后將其導入ADAMS中，如圖4所示，并將給定的運動規律添加到動平臺2中心點。其中在ADAMS中，添加的驅動為一般點驅動。

圖4 ADAMS虛擬樣機模型

逆解模型的仿真結果如圖5(a)所示。根據式(11)，利用MATLAB編程，并繪制出(=1,2,3)桿長變化曲線，如圖5(b)所示。

圖5 反解模型計算和仿真結果對比

從圖5(a)和圖5(b)可以看出:兩者(=1,2,3)變化曲線高度吻合，從而驗證了運動學反解模型的正確性。

4.2 正解模型

給定3個滑塊移動驅動運動規律如下：

(14)

在ADAMS中，給定3個滑塊的移動驅動，然后仿真求解動平臺2的位姿如圖6(a)、圖6(b)所示。根據式(12)，采用牛頓迭代法，在MATLAB中編程。其中，給定的初始值為(0 0 177.8),求解精度為1×10。繪制動平臺2位姿曲線如圖6(c)、圖6(d)所示。

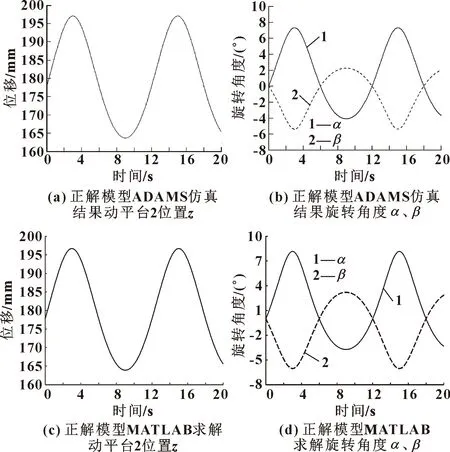
圖6 正解模型計算和仿真結果對比

從圖6(a)和圖6(c)可以看出:兩者動平臺2中心點的位置變化曲線高度吻合；從圖6(b)和圖6(d)可以看出:兩者旋轉角度、變化曲線高度吻合，從而驗證了運動學正解模型的正確性。

5 混聯機構動平臺2運動范圍分析

前面運動學分析都是基于支鏈1、支鏈2、支鏈3桿長保持固定不變，這樣做的目的是便于分析該混聯機構的正解、逆解。但是，為了增加動平臺2的運動范圍，可以讓一個電機同時驅動支鏈1、支鏈2、支鏈3到達一定的高度保持不變，然后在這一高度下，再次進行混聯機構的正解和逆解的分析，分析方式和前面一致，只是豎直方向的位移發生了變化而已。理論上，當只有支鏈1、支鏈2、支鏈3驅動，則該混聯機構動平臺2中心點″豎直方向的位移可在71.57～221.57 mm內變化。而前面的運動學分析，是動平臺2中心點″在定坐標系下，方向為177.80 mm(初始位型)下的正解、逆解而已。

當仍采用式(14)運動規律時，動平臺2運動范圍如圖7所示。可以看出：該混聯機構的動平臺2具有較大的運動范圍，使該混聯機構得到了最大化利用。

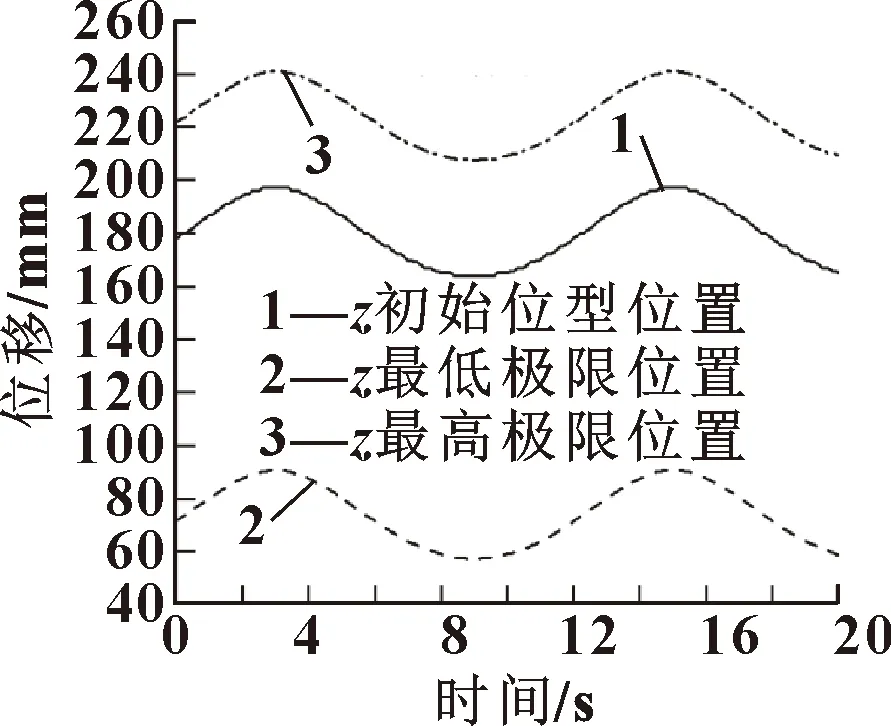
圖7 動平臺2運動范圍

6 結論

(2)通過余弦定理、空間坐標變換法和牛頓迭代法等建立該混聯機構運動學分析的逆解模型和正解模型，并在SolidWorks中建立該混聯機構三維模型，再將其導入ADAMS中進行仿真驗證。驗證結果高度吻合，證明了混聯機構逆解模型和正解模型的正確性。

(3)提出了一種3-PRS & 3P混聯機構，并對其動平臺2的運動范圍進行了分析，分析結果表明：該混聯機構動平臺2具有較大的運動范圍。