熱流固耦合下微觀織構配流副摩擦特性的研究

王宇帆，王兆強，張嬌

(上海工程技術大學機械與汽車工程學院，上海 201620)

0 前言

配流副是軸向柱塞泵的關鍵摩擦副之一，但是在軸向柱塞泵的運行過程中，配流盤的功率損失高達8%。功率損失的主要來源是潤滑界面的摩擦損失和泄漏損失，尤其在低速情況下，由于壓力較低，泄漏量較小，摩擦損失占功率損失的絕大部分。摩擦損失一方面取決于潤滑油的黏度，另一方面也與配流副摩擦表面形貌和材料有關。隨著對柱塞泵性能要求的提高，業內普遍認為表面織構技術在提高柱塞泵效率和承載能力方面起到積極作用。

HAMILTON等利用實驗的方法驗證了材料表面的微凸起織構能改善潤滑性能，他推測微凹坑織構也能產生同樣的效果。清華大學汪家道等研究了面接觸下不同尺寸的規則凹坑織構對表面摩擦性能的影響，對比了4種不同形貌織構的面接觸摩擦潤滑實驗結果，認為微凹坑的面積率是影響摩擦性能的主要因素。王霄等人利用多重網格法求解了帶有微觀織構表面的潤滑模型，研究發現球冠型織構產生的潤滑油膜壓力大于圓柱形和圓錐形織構。馬晨波研究發現微觀織構的深徑比在0.005～0.01時具有更好的潤滑性能。同年，中科院蘭州化學物理研究所胡天昌等對表面織構化的45號鋼進行摩擦實驗，結果發現：與未進行織構化的材料相比，帶有微觀織構表面的材料能有效減小摩擦因數，且磨損率也有一定的降低。2013年，中國礦業大學朱華等人在研究微凹坑對摩擦副摩擦性能的影響時發現：當微凹坑織構的面積率在5%時能產生最大的流體動壓承載力。韓國學者SEGU D Z及其團隊將不同形狀的微觀織構(圓形、正方形、三角形、橢圓形)混合排列加工到試件表面，并進行不同的排列組合，進行摩擦學實驗，結果發現：帶有微觀織構的試件均能不同程度地降低摩擦因數、減少磨損。近年來，隨著對微觀織構配流副的理論研究越來越深入，人們發現熱流固耦合條件下，微觀織構能顯著改變配流副油膜壓力和溫度的分布。

本文作者基于Reynolds方程建立帶有方形微觀織構配流副的潤滑模型，運用有限差分法進行求解，得到離散的壓力值、彈性變形和溫度值，通過迭代耦合得到誤差允許范圍內的近似解，并將求得的解導入到MATLAB繪制分布云圖，最后改變織構參數分別進行求解，分析了織構參數對潤滑性能的影響。

1 建立微觀織構配流副潤滑模型

在構建帶有微觀織構配流盤的配流副時，忽略配流盤表面的粗糙度而假定除織構區域外的配流盤表面為絕對光滑。柱塞泵在工作狀態下，由于缸體相對于配流盤轉動，缸體受到偏載力矩的作用，會向一側傾斜一定角度。如圖1所示，缸體傾斜角度為，配流盤與缸體之間的初始距離為；缸體繞軸逆時針繞轉，轉速為；矩形織構均勻分布在配流盤表面，深度為，邊長為。

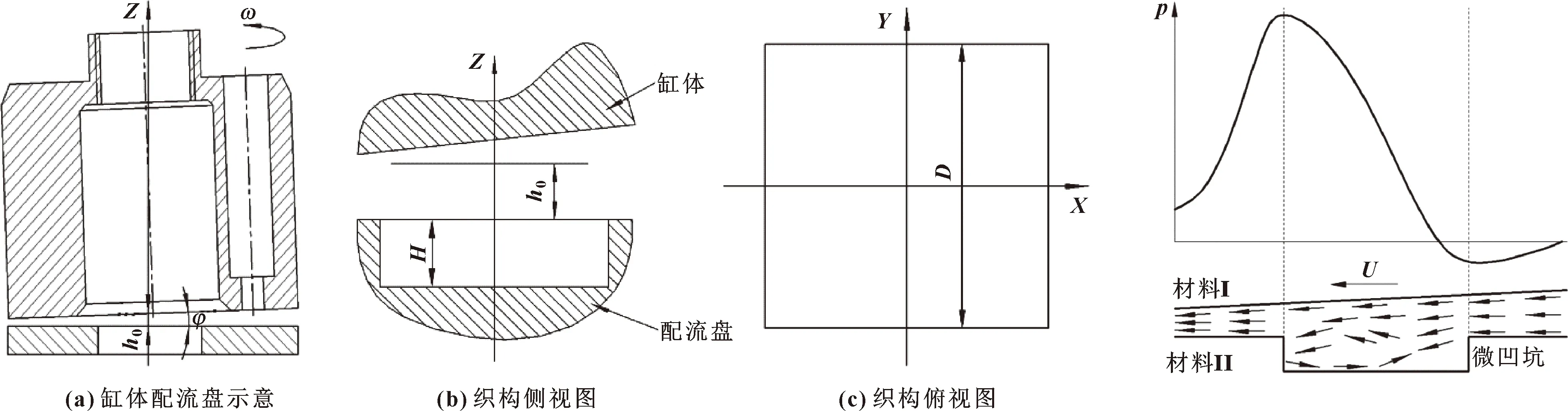
圖1 微觀織構配流副結構模型 圖2 微觀織構引起的流體動壓效應

矩形織構參數是通過潤滑油膜厚度引入的。在織構的計算區域內，不同的織構參數對應油膜厚度不同，由于流體的動壓效應，導致壓力分布不均勻，進而影響油膜的摩擦特性，如圖2所示。

2 理論模型的計算

2.1 油厚方程

由圖1所示的配流副模型可知缸體相對于配流盤旋轉，并發生一定角度的傾斜，此時油膜呈楔形圓環狀。為方便計算，將后續求解運算過程均轉化為圓柱極坐標系，油厚方程可表達為

=+·sin·tan

(1)

2.2 Reynolds方程

由于此研究中的Reynolds方程是由不可壓縮流的Navier-Stokes方程推導而來，所以在求解之前，需要對配流副中的油膜進行必要的假設：(1)忽略油膜慣性力和體積力；(2)流體與固體間無相對滑移；(3)由于油膜厚度極小，忽略油膜厚度方向上的壓力變化，由此引申為忽略油膜厚度方向上的溫度、黏度變化；(4)潤滑油為牛頓流體；(5)忽略由于壓力、溫度引起的潤滑油密度的變化。

此時極坐標下的Reynolds方程為

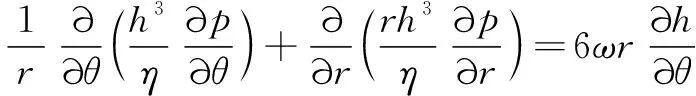
(2)

式中：為油膜壓力；為潤滑油黏度；為網格節點處的半徑值；為油膜厚度；為網格節點處的角度值。

離散化后運用有限差分法得到解為

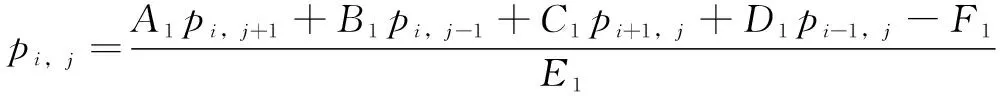
(3)

其中：

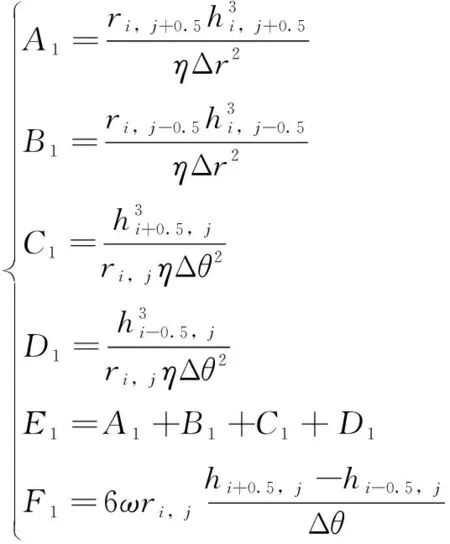
(4)

邊界條件為油膜邊界壓力值為大氣壓。

2.3 能量方程

二維能量方程可寫成下面形式：

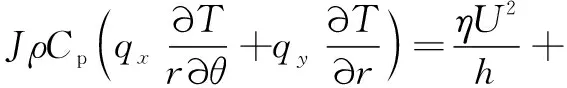
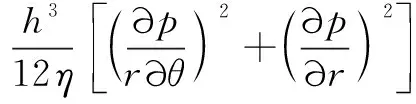
(5)

式中：為熱功當量；為潤滑油密度；為比熱容；為油膜溫度；為兩摩擦表面平均速度；、分別為、方向上的體積流量。

離散化后運用有限差分法得到解為

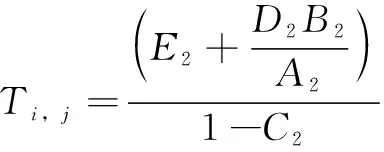
(6)

其中：

(7)

邊界條件為油膜邊界隔熱且初始溫度為環境溫度。

2.4 彈性變形方程

配流盤是一個圓環形的厚板結構，由于受到表面油膜的壓力，配流盤的表面將產生垂直變形，其變形量可以從彈性變形理論得到解釋，得到彈性變形方程寫作如下形式：

(8)

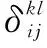
壓力分布對彈性變形的影響如圖3所示。

圖3 壓力分布對彈性變形的影響

但是式(8)在點=且=時存在奇異點。為避免奇異點，用奇異點附近的一點(=，=-1)代替奇異點，即：

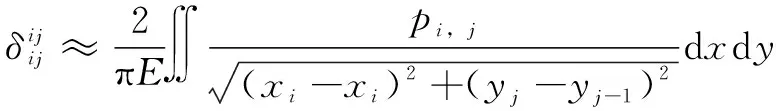
(9)

離散化后得到總位移變形,為

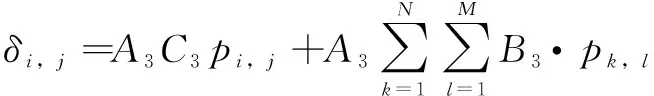
(10)

其中：

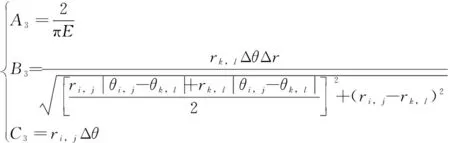
(11)

2.5 黏溫-黏壓方程

在計算熱流固耦合的潤滑模型時，需要考慮到溫度和壓力對潤滑油黏度的影響。描述黏度和壓力、溫度變化規律的方程主要有3種：Barus公式、Roelands公式和Cameron公式。其中Roelands公式公認精確度最高，且數值計算穩定性強，其表達式為

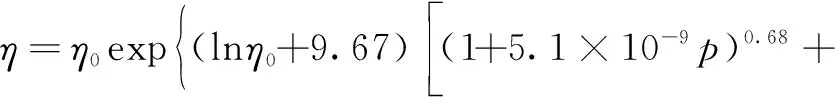
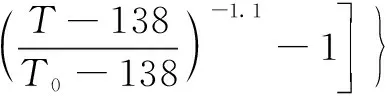
(12)

3 油膜潤滑特性

為了計算配流副油膜的潤滑特性，給定初始工作條件如下：缸體轉速=3 500 r/min；初始油膜厚度=0.032 5×10m；缸體傾斜角度=0.004°；潤滑油黏度=0.036 5 Pa·s；環境溫度=303 K；微觀矩形織構邊長=200 μm；深度=5 μm；織構沿圓周方向均勻排布120個，沿半徑方向均勻排布10個，共計120×10個。

將計算結果導入到MATLAB，繪制出油膜壓力分布云圖如圖4所示，彈性變形分布云圖如圖5所示，油膜溫度分布云圖如圖6所示。

圖4 油膜壓力分布 圖5 彈性變形分布 圖6 油膜溫度分布

4 織構參數對潤滑特性的影響

在理想的平行光滑平面的摩擦副中，兩平面間的潤滑油膜由于沒有收斂間隙，無法產生流體動壓承載力，但是微觀織構的存在使得微觀織構邊界處客觀上存在一個類似的收斂間隙，為流體動壓承載力的存在提供了基礎。但是不同的織構參數會怎么影響潤滑特性？作者將織構邊長劃分為50、100、150、200、250、300、350 μm，織構深度劃分為5、10、20、50、80、100、120、150、200 μm，并逐一進行仿真，來探究不同的織構參數對油膜的潤滑特性產生什么樣的影響。

圖7顯示的是矩形織構參數對油膜承載力的影響。在不同織構邊長的情況下，隨著織構深度的增加，油膜的承載力先增加后減小，最大承載力在織構深度20～50 μm之間，且織構邊長越大，承載力越大。但是可以注意到，織構邊長越大，其最大承載力對應的織構深度越小，呈現向左移動的現象。

圖7 織構對油膜承載力的影響 圖8 織構對摩擦力的影響 圖9 織構對摩擦因數的影響

圖8顯示的是矩形織構參數對摩擦力的影響。在不同織構邊長的情況下，隨著織構深度的增加，摩擦力整體呈現減小的趨勢，且織構邊長越大，摩擦力會越小。

圖9顯示的是矩形織構參數對摩擦因數的影響。在不同織構邊長的情況下，隨著織構深度的增加，摩擦因數整體呈現先減小后增大的趨勢，最小摩擦因數在織構深度20～50 μm之間，且織構邊長越大，摩擦因數越小。

5 結論

(1)從壓力分布圖(圖4)中可以看出：由于缸體傾斜，潤滑油在一側形成楔形間隙，出現了流體動壓效應，使得壓力呈單峰形態集中在一側。同時注意到：在矩形微觀織構的邊緣，由于油膜厚度的急劇減小，使得油膜出現類似楔形的狀態，為動壓效應的出現提供了條件。而結果也確實如理論預測的一樣，在潤滑油表面出現規則排布的壓力峰值。

(2)從圖7—圖9發現：織構邊長越大，油膜的潤滑特性越好。但是應當注意的是，不同邊長的織構對應的最佳織構深度并不相同，隨著邊長的增大，其最佳深度在減小，最佳深度范圍在20～50 μm之間。整體而言，織構越大，摩擦力越小，摩擦因數越小。

(3)本文作者僅從織構的大小、深度方面來考慮其對配流副油膜潤滑特性的影響，可以預料的是織構的形狀、個數、排列方式等也會對潤滑特性產生影響，需要更多的計算結果去支持這一猜想。