基于模型重構的凸輪加工在線補償方法

杜柳青, 李祥，呂發良，余永維

(重慶理工大學機械工程學院，重慶 400054)

0 前言

高精度凸輪加工采用CNC控制的-軸聯動高速磨削，高端數控磨床上都帶有位移補償裝置，想要進一步提升凸輪加工精度，就必須降低-軸聯動加工的同步誤差，而降低同步誤差的最好方式是對加工過程進行閉環微分補償。-軸聯動加工模型實現微分補償需要計算模型導數，而模型的數學公式非常復雜，導數計算難度和計算量都非常大，在高速加工過程中無法確保數據能夠進行實時交互。如何簡化模型成為實現在線補償的一個關鍵問題。

國內外學者對凸輪-軸聯動加工進行了大量研究。陳硯坤等應用-軸聯動模型設計了凸輪輪廓誤差迭代器。隋振等人研究了分別以仿形誤差、切向輪廓位置誤差、等效誤差算法等方式進行的加工補償。劉偉等人設計了凸輪加工位移檢測實驗平臺。張培碩等研究了凸輪磨削砂輪磨損誤差對凸輪加工的影響。孫海峰等對凸輪在線檢測加工工藝進行了一系列研究。程智勇針對圓柱凸輪，提出了一種采用線性誤差進行控制的四軸加工方法，與傳統的加工方法相比，加工精度明顯提升。

現有研究均先分析凸輪-軸聯動加工數學模型，然后進行加工補償。這種補償方式僅考慮了理論情況下凸輪輪廓的變化情況，而實際加工中其他因素導致的加工誤差并未被消除。如果考慮所有因素帶來的誤差會使數學模型非常復雜，不利于計算。實際加工通常都是對單級運動進行反饋補償，而消除凸輪-軸聯動加工同步誤差的研究較少。

為解決上述問題，提出一種凸輪加工檢測及補償方法。利用該方法，在加工的同時可檢測凸輪輪廓信息并反饋至終端，然后終端經-軸聯動加工模型計算后反饋給NC，實現閉環補償。實際的-軸聯動加工速度非常快，所以本文作者針對這一特點，通過分析升程和速度瞬心數學關系，重構-軸聯動加工數學模型，取得了較好效果。

1 凸輪加工補償數學模型

為得到凸輪加工補償的數學模型，首先要對已有的-軸聯動模型進行分析，以找到一個可行的簡化方法。

1.1 磨削時X-C軸聯動加工數學模型

進行凸輪磨削加工時，一般提供的是凸輪升程表，或者是輪廓曲線方程()。通常情況下，輪廓曲線方程和升程表是可以相互轉換的。升程表的優點是加工時只需要輸入升程數據，然后由數控系統自動完成插補；而輪廓曲線方程的優點是理論計算推導時無需擬合輪廓曲線。在實際加工時，為得到規則化輸出，通常采用擬合輪廓曲線的方式。

凸輪的升程表是根據工作狀況給定的，分為滾子、平頂、尖頂3種從動件，為方便分析，統一用1個滾子代替3種從動件。如圖1所示，以為圓心、為半徑的圓為工作從動件，=0、=∞、=分別代表尖頂、平頂、滾子3種從動件的半徑；為砂輪半徑；為砂輪圓心；為基圓半徑；為凸輪圓心；為工作轉角；為加工轉角；為加工狀態轉角；點為工作狀態下的速度瞬心。

圖1 凸輪X-C軸聯動加工模型

由速度瞬心的相關關系可以推導出：

(1)

=++()

(2)

式中:()為輪廓曲線方程。

令=∠，則:

(3)

在△中,由余弦定理可得：

(4)

為磨削點的極半徑大小，用來表示：

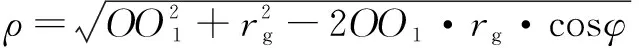
(5)

最終可得：

(6)

得到-軸聯動加工模型如下：

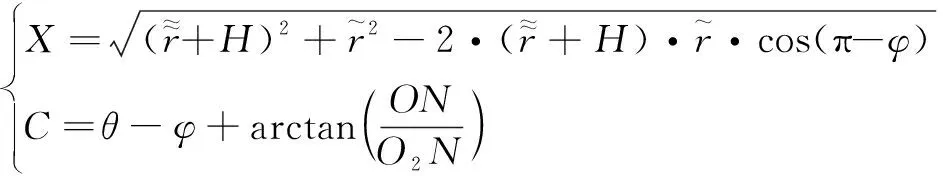
(7)

1.2 模型重構

凸輪加工時通常是將升程數據直接存儲到NC系統中的升程表中，則補償數據也應以同樣形式存儲到補償表中。對-軸聯動模型求導得到如下補償模型:

(8)

其中：

式中:Δ為測頭檢測出的實際量與理論升程差值，Δ為軸補償量，Δ為軸的補償量。

從公式(8)可知,補償數據計算非常復雜，涉及升程的一階微分運算和大量的平方和開根號。在實時動態補償過程中需要做到毫秒級的計算速度，上述公式在NC系統中無法達到這一要求。

根據凸輪工作狀態的不同,升程和補償數據的計算方式不同，當平頂作為從動件時速度瞬心和圖1中垂足點剛好重合，當兩點重合后模型的幾何關系與參數量都得到了大幅簡化；而不同工況的升程間可以互相轉換，將所有工況的凸輪升程全部轉化為平頂工況，采用平頂測頭進行在線測量就可以使用簡化模型來補償。簡化后的模型如圖2所示，為凸輪軸圓心；為砂輪圓心；為工作狀態轉角；為加工狀態轉角；點為工作狀態下的速度瞬心。

圖2 凸輪X-C軸聯動加工重構模型

在△中,由幾何關系可得：

(9)

=--

(10)

(11)

=++()

(12)

(13)

由圖2中角的關系可得：

=+

(14)

(15)

綜合可得：

(16)

由此得到最后的簡化模型：

(17)

2 基于模型重構的在線補償

2.1 凸輪升程轉換

簡化模型是在平頂從動件的基礎上推導而來的，但多數情況下升程數據并非一定是平頂工況的，所以還需要對不同工況下的升程數據作相應轉換。圖3所示為不同工況下升程與轉角的關系。

圖3 不同從動件下的升程示意

圖4中，為滾子圓心、為滾子半徑；為平頂工況下轉角；為加工轉角；為滾子工況下轉角。

圖4 X-C軸聯動凸輪升程轉換模型

假設平頂工況下升程定義為

=-

(18)

滾子工況定義為

=--

(19)

又由于+=·cos，最后化簡得：

=(++)·cos--

(20)

點為滾子工況下的速度瞬心，∠=∠+∠，由速度瞬心定理可得：

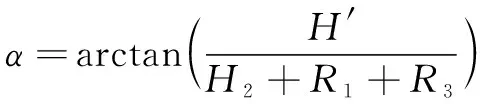
(21)

綜合以上公式可以得到升程轉換公式如下：

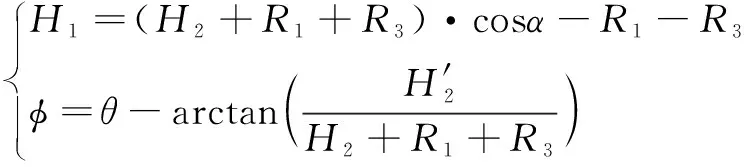
(22)

當升程為尖頂從動件時，令=0。

2.2 在線補償方法

計算簡化模型的微分形式就可以得到簡化的在線補償模型，補償微分公式如式(23)所示：

(23)

數控系統中補償表使用的是平均間隔增量數據，然而從補償公式中得到的是不規則間隔數據，即角度+Δ對應的升程為+Δ，微分算子導致了間隔不可能相同。為得到規則化的補償數據，可以通過最小二乘法擬合得到原曲線方程，然后通過曲線方程得到規則化的升程數據。

本文作者擬采用的在線補償方式是通過凸輪前一輪加工的檢測數據對下一輪加工進行補償。這種補償方式需要模型有極高的靈敏度。而簡化模型最大的優勢就是模型復雜度低，計算中用到的一階和二階微分都可以在加工之前計算存儲到系統中，極大地減少了計算量，避免了計算滯后，為實時補償提供了保障。

在實際補償時，由于會用到前一輪的檢測數據，而初始加工時是沒有檢測數據的，所以第一輪的加工是不帶補償的。基于這一特點，該補償方式叫做延遲補償模式。延遲檢測補償的工作原理是凸輪加工前一輪的檢測數據經過模型計算得到補償后，疊加到下一輪的加工中。延遲補償工作過程如圖5所示，凸輪經過多輪加工后得到最終輪廓曲線。

圖5 延遲補償過程示意

3 實驗驗證及分析

本文作者對小基圓凸輪加工的檢測數據進行模擬驗證。首先，根據升程表繪制凸輪的散點圖，以觀察輪廓曲線變化趨勢，如圖6所示。然后，根據-軸聯動數學模型得到聯動加工曲線圖，如圖7所示，該曲線為理論輪廓曲線的參考曲線。

圖6 升程散點 圖7 X-C軸聯動數據曲線

在高速外圓磨床HBW23-P上對該凸輪進行磨削檢測實驗，并在線檢測記錄每輪磨削后的實際輪廓，隨機抽取一輪檢測結果，繪制出實際與理論輪廓的對比圖，如圖8所示。

圖8 檢測對比

以相同條件進行磨削補償實驗，隨機抽取一輪補償測試結果數據與檢測數據作對比，如圖9所示。可以看出：經過補償后，每輪的平均誤差都會減小，凸輪輪廓更接近理論的輪廓曲線，驗證了文中補償方法能夠有效提高凸輪的磨削精度。

圖9 補償測試結果與檢測結果對比

4 總結

本文作者通過分析現有-軸聯動加工模型，提出了補償模型重構的方法。該重構模型與原模型相比較，算法復雜程度更低，降低了計算補償數據的時間，使它能夠很好地運用在實際的凸輪檢測補償加工中；結合升程轉換理論，使這種模型可以普及到不同從動件工況的凸輪加工中，最終得到通用的補償模型；通過延遲補償模式，實現了在線檢測補償功能，通過實驗驗證了該模型的有效性。