凸轉子定點共軛的極限輪廓構造及輕量化分析

2022-09-21 08:29:12陳曦劉嘉

機床與液壓 2022年17期

陳曦，劉嘉

(1.重慶化工職業學院，重慶 401220；2.太原工業學院機械工程系，山西太原 030008)

0 前言

凸轉子泵是利用兩個相同凸轉子在旋轉過程中所產生的進口真空吸力，將介質輸送到出口的一類容積泵，應用廣泛。其中，轉子副廣義上分為接觸式(如齒輪泵)和非接觸式(如羅茨泵)兩類，轉子的容積利用系數是衡量該類泵輕量化效果、流量脈動性能的最重要指標之一，如形狀系數越大，容積利用系數(≈1-1/)越大，泵的單位體積排量就越大，額定排量下的“轉子體積/質量∝1/”就越低，即輕量化效果越好。對于具有頂偏心圓弧過渡的常見普通轉子，其形狀系數由轉子輪廓中共軛段的形狀直接決定。其中，共軛段由節圓外共軛段和節圓內共軛段兩部分組成；由普通轉子經高形化改進后得到的高形轉子，其轉子形狀系數可進一步提高。針對共軛段所采用的不同曲線類型，目前雖然已有各自最大形狀系數的通用判據及計算方法，但是并沒有解決共軛段為何曲線類型時能取得所有曲線類型中的極限形狀系數問題。為此，旨在由內共軛段收縮為一定點時的輪廓構造條件，直接計算出轉子能取得的該極限形狀系數，并由此確定出外共軛段的曲線方程，并針對其高形化應用作進一步研究。

1 內外共軛段形狀隨形狀系數的變化規律

在現有普通轉子中，漸開線轉子具有較大的形狀系數。以三葉漸開線普通轉子為例，1.20、1.35、1.46三種形狀系數下的半葉外共軛段和內共軛段，如圖1中的Ⅰ、Ⅱ、Ⅲ所示。其中，其極限形狀系數為1.46，由于漸開線構造原理上的特殊性，外共軛段和內共軛段為一條完整的漸開線段。

圖1 共軛輪廓段間的雙對稱關系

設轉子中心為，節圓半徑為，轉子葉的峰、谷對稱軸與節圓的交點分別為峰節點、谷節點，間節圓弧的圓心角為2=π/，為轉子葉數，中軸為峰、谷對稱軸間的角平分軸，且中軸過節點，葉頂部、谷部采用圓心為峰節點、谷節點的過渡圓弧段，即為最常見的普通轉子。此時轉子頂過渡圓弧面(圓心非)與泵殼內腔圓弧面(圓心為)形成的徑向間隙為非等間隙，徑向泄漏較大。

圖1中，設點、為節圓上關于中軸對稱的2個點，對應圓心角為，0≤≤，點、在漸開線段上的法向垂足分別為點、。

由兩相同轉子間的共軛原理，知、的連線具有相同的長度,設為();連線與連線間、連線與連線間具有相同的夾角,設為()。

此時顯然連線關于中軸的對稱線為′連線；連線關于節圓切線′的對稱線也為′連線，即連線和連線具有先關于點處節圓切線互為對稱和后關于中軸互為對稱的幾何關系。利用這種關系的輪廓構造方法稱為雙對稱構造法，如圖1所示。

在圖1所示坐標系下，外共軛段和內共軛段的坐標方程(0≤≤)分別為

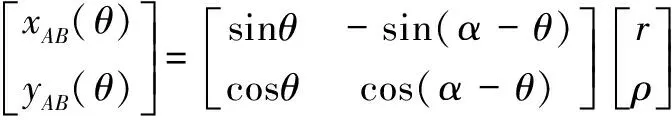
(1)

(2)

式中:(,)、(,)分別為圖1中外共軛段、內共軛段上點、點的坐標。

由外共軛段和內共軛段在1.20、1.35、1.46三種形狀系數下的變化規律，知越大，內共軛段向節點逐步收縮聚集的趨勢越大，當收縮匯聚為節點時，稱之為定點共軛。相應地，應取得普通轉子各種曲線類型下的極限形狀系數，否則，將因內共軛段位于節圓外，不能形成轉子副正確的共軛幾何關系，如圖2所示。

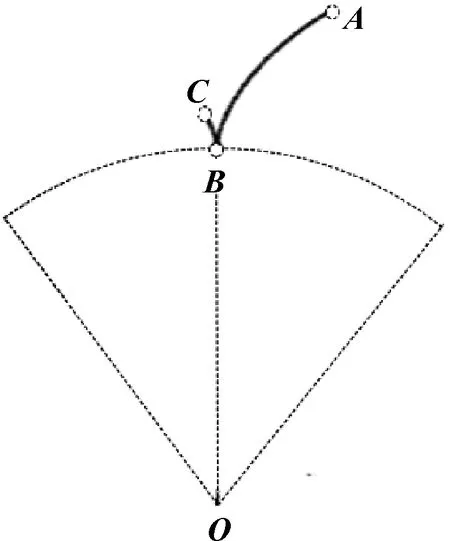
圖2 內共軛輪廓段的幾何干涉

2 定點共軛普通轉子的輪廓構造及形狀系數

圖1中當內共軛段收縮匯聚為節點時，對應的普通轉子半葉輪廓如圖3所示。此時，由等腰△的幾何關系得:

(3)

將式(3)代入式(1)，則外共軛段在圖3所示下的坐標方程為

圖3 定點共軛普通轉子的輪廓構造

(4)

將=代入式(3)，得定點共軛普通轉子的形狀系數為

(5)

由文獻[12]容積利用系數計算式的進一步推導，得定點共軛普通轉子的容積利用系數為

(6)

三葉下的驗證如圖4所示。其中，驗證采用UGNX軟件中的面積測量工具。

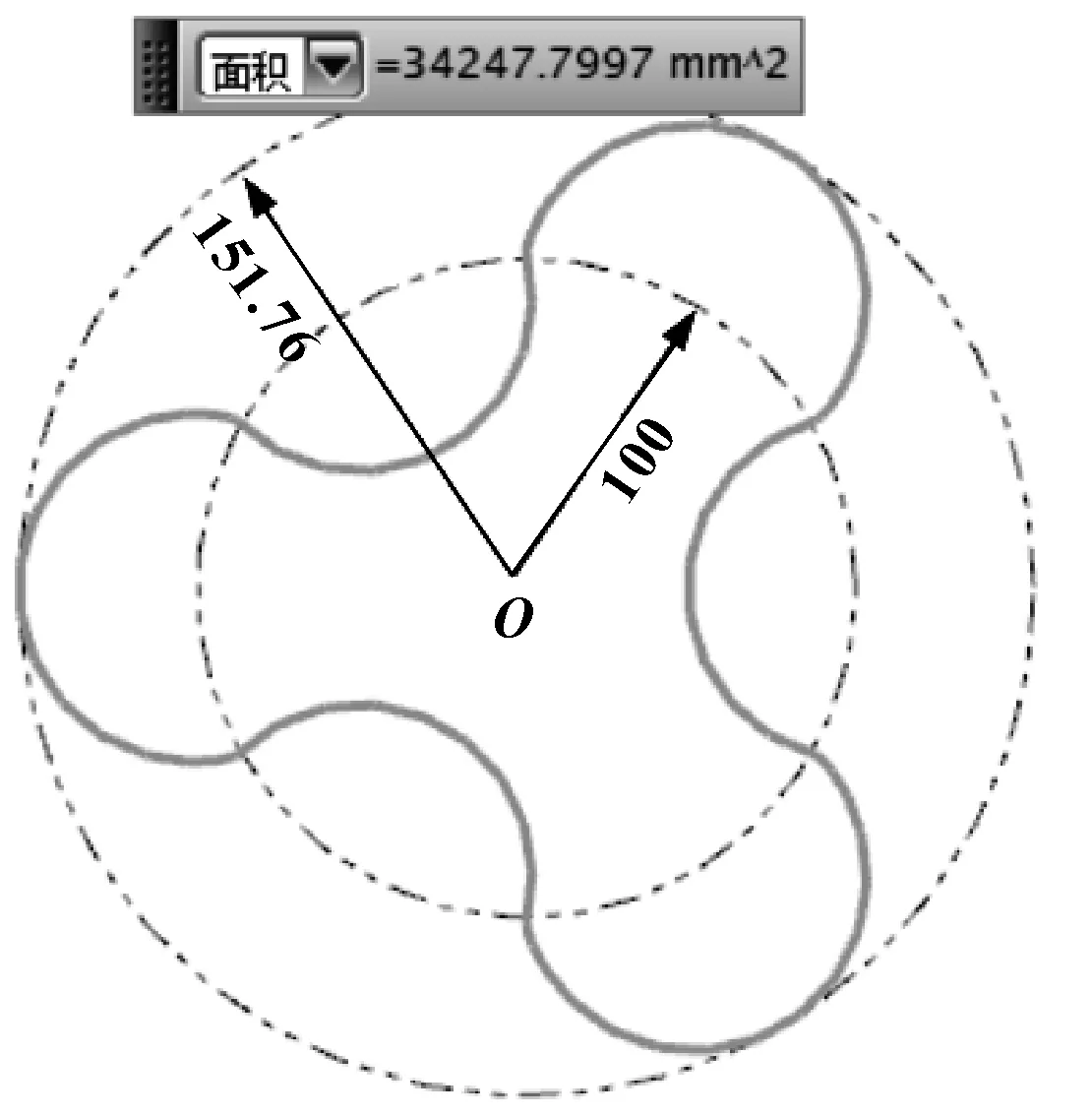
圖4 三葉定點共軛普通轉子模型

由圖4測量出：

(7)

式(7)結果與式(5)—式(6)完全一致，說明式(1)—式(6)正確。

漸開線普通轉子的最大形狀系數及其最大容積利用系數分別為

(8)

由式(8)知二、三、四葉定點共軛普通轉子的形狀系數與普通轉子相比分別提高了9.13%、3.68%和1.81%，容積利用系數分別提高了8.06%、5.38%和3.72%。

3 定點共軛高形轉子的輪廓構造及形狀系數

為充分控制定點共軛普通轉子頂部的徑向泄漏和緩解排氣側壓縮反沖現象對該徑向泄漏的影響，可采用如圖5所示的定點共軛結合頂同心圓弧段的高形輪廓構造，與相共軛的谷圓弧段為。其中，頂同心圓弧段、谷圓弧段的圓心均為轉子中心，半徑為、(2-)，圓心角均為頂封角，因能大幅度提高普通轉子的形狀系數，故稱之為定點共軛高形轉子。

圖5 定點共軛高形轉子的輪廓構造

圖5中，取對應于>的節圓點為，并由控制的變化上限。

根據等腰△的三角幾何關系，邊的長度和角∠分別為

(9)

由△中的幾何關系，得邊的長度和角∠分別為

(10)

由轉子與配對轉子完全相同和轉子副旋轉過程中的輪廓點恰好避讓配對轉子上的輪廓點的輪廓構造，得=及∠=π-2∠，即∠=∠+ ∠=π-∠。

聯立式(9)和(10)，得定點共軛高形轉子的形狀系數和頂封角分別為

(11)

再由容積利用系數計算式進一步推導，得定點共軛高形轉子的容積利用系數為

(12)

其中，=3下()、()、()的變化規律如表1所示。

表1 高形轉子形狀系數和頂封角及容積利用系數

以三葉=55.9°的定點共軛高形轉子為例，其模型如圖6所示。此時形狀系數=1.660 6、容積利用系數=0.604 5，相較于定點共軛普通轉子的形狀系數=1.517 6、容積利用系數=0.526 7，高形轉子的形狀系數再提高9.42%，容積利用系數再提高14.77%。相較于具有上限形狀系數的三葉漸開線普通轉子的形狀系數=1.463 8、容積利用系數=0.499 8，形狀系數總提高13.44%，容積利用系數總提高20.95%。