基于相關系數稀疏表征的轉子振動信號周期特征提取
唐振宇,黃凱,楊期江,朱曉彬
(廣州航海學院船舶與海洋工程學院,廣東廣州 510725)
0 前言
在旋轉機械轉子系統的運行過程中,因受到測試環境、測試儀器和人為因素等影響,傳感器所采集的振動信號易被噪聲污染,且旋轉機械結構復雜,振動信號往往由多個部件的振動疊加而成。轉子振動信號具有非高斯、非平穩的特性。傳統的信號處理方法對含有噪聲的混疊信號進行分析時有明顯不足,這也對機械的狀態監測和故障診斷帶來了巨大的困難。
傳統的信號處理方法如小波分解、經驗模態分解(Empirical Mode Decomposition,EMD)已被廣泛應用于旋轉機械振動信號分析,但對于含噪的混疊信號,上述方法仍存在明顯不足。小波分解在對轉子振動信號分析時存在以下問題:(1)小波分解層數的確定需要信號的頻率結構和采樣頻率等先驗知識;(2)小波基和閾值的選擇困難。經驗模態分解也存在模態混疊和端點效應問題,導致基于EMD的方法效果不佳。改進的EMD方法如集合經驗模態分解(EEMD)是將噪聲輔助分析加在經驗模態分解中,有效地抑制了模態混疊的現象,但無法完全消除混疊現象。因此對于信號的分解,應該根據信號本身的結構特點,自適應選擇基函數完成信號的分解。1993年MALLAT和ZHANG提出了基于過完備字典對信號進行稀疏分解的思想,同時也提出了匹配追蹤算法。2004年有學者建立了壓縮感知理論(Compressing Sensing,CS)。壓縮感知理論證明了信號在某個變換空間內具有稀疏性,可僅用少量數據保留信號的大部分特征,這樣可以用遠低于奈奎斯特采樣定理要求的采樣頻率完成信號的重建恢復,這也將稀疏分解帶到了一個新高度。稀疏分解存在稀疏度過大,重構信號的噪聲分量增加,而稀疏度過小,重構信號又會丟失重要特征信息的問題。其中,稀疏度為信號中非零元素的個數。針對稀疏度選取問題的研究,文獻[6]提出了稀疏度自適應匹配追蹤算法(Sparsity Adaptive Matching Pursuit,SAMP),文獻[7]提出變步長自適應匹配追蹤算法,文獻[8]提出基于CS的稀疏度變步長自適應壓縮采樣匹配追蹤算法。
對于稀疏度的研究,國內學者大多是對SAMP算法進行改進。本文作者提出互相關稀疏分解的方法,將互相關函數引入稀疏分解中以凸顯稀疏分解后各分量與原信號之間的相關性,并計算相關系數以解決稀疏度的選取問題。采用所提方法進行仿真實驗和轉子振動信號實例分析,成功提取振動信號周期特征。
1 互相關稀疏分解原理
1.1 信號的壓縮感知
以轉子系統為核心部件的旋轉機械運行工況復雜,傳感器采集到的信號含有大量噪聲。轉子振動信號數學模型為
()=()+()
(1)
式中:()為轉子振動信號;()為噪聲。對于實信號(),如果它在稀疏字典中是稀疏的,則用觀測矩陣對信號進行壓縮傳感,得到觀測信號。壓縮傳感方程表示為
=
(2)
有效的壓縮傳感要求觀測矩陣與稀疏字典互不相關,否則無法求解。高斯矩陣是壓縮傳感常用的測量矩陣,滿足RIP性質。
1.2 稀疏分解理論

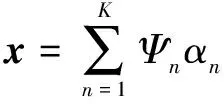
(3)
其中:為每個字典原子相對于原信號的權重,集合為稀疏系數,且只有個非零值。
1.3 正交匹配追蹤算法
常見的自然信號在時域是不稀疏的,信號稀疏分解理論指出,信號可以經過變換矩陣進行稀疏表示。由式(2)可以看作原信號在觀測矩陣下的線性投影,顯然的維數遠低于的維數,用進行稀疏分解更為容易。結合式(2)(3)得出下式:
=α
(4)
式中:=為×的矩陣(?),稱為感知矩陣。此時滿足約束等距條件,可以通過求解式(5)的最優化范數式重構信號。
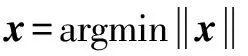
s.t.=
(5)
式(5)本質上是一個優化問題,即NP-hard問題。本文作者利用正交匹配追蹤算法(Orthogonal Matching Pursuit,OMP)選取多個字典原子計算信號最優逼近,使得誤差最小。OMP通過求殘差與感知矩陣中各個原子之間內積值的絕對值,來計算稀疏系數。內積的絕對值越大說明感知矩陣中的這一列原子與信號越相關。
={|=|〈,〉|,=1,2,…,}
(6)
并采用最小二乘法對信號進行逼近和殘差更新:

(7)
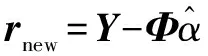
(8)
OMP算法具體步驟如下:
(1)初始殘差=,迭代次數=1,索引值集合=、=;
(2)計算殘差與感知矩陣中各個原子之間內積值的絕對值,并將中的最大值對應的索引值存入中;
(3)更新感知矩陣,其中=∪;
(4)應用公式(7)得到,同時用式(8)對殘差進行更新;
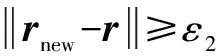
1.4 過完備字典構造
過完備字典是一組具有廣泛時頻特性的函數波形,每個波形作為字典中的一列,這一列稱為原子,原子的數量是冗余的。基于過完備字典的稀疏分解能夠根據信號的結構特征提取信號的各種局部特征,實現信號的自適應分解,獲得信號的稀疏表示。
針對轉子振動信號的周期特征,構造離散傅里葉變換矩陣(Discrete Fourier Transform,DFT),長度為的轉子振動信號()通過DFT矩陣變換后轉化為()的形式:

(9)
即=,上述過程表示為矩陣形式為式(10)

(10)
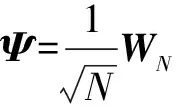
(11)
公式(11)將其歸一化后可得到過完備字典。
1.5 皮爾遜相關系數
皮爾遜相關系數是用于度量2個向量之間線性相關性的變量,計算公式為

(12)
其中:為信號的點數;為[-1 1]之間的數,越接近于1,則2個變量之間的相關性越高。
采用皮爾遜系數作為稀疏分解效果的評判標準。計算稀疏分解后的信號與原信號的相關性。一般情況下,當>0.7時,認為稀疏分解的信號與原信號相關性好,是真實的分量,予以保留。
2 仿真實驗及分析
轉子振動信號波形復雜,由其轉頻及倍頻和隨機噪聲等組成。依據上述特點,構造仿真信號(),設置采樣頻率=2 000 Hz,采樣點數=1 200,則有:
()=sin(2π)+sin(2π)+sin(2π)+()+()
(13)
()=e-sin(2π)
(14)
其中:為轉子轉頻;、分別為2倍頻和3倍頻;()為轉子正常運行時產生的沖擊衰減分量;()為均值為0且方差為1的高斯白噪聲。
設幅值=2 mm、=1.6 mm、=1.2 mm、=0.2 mm、=50 mm;基頻=30 Hz; 倍頻、分別為60、90 Hz;沖擊頻率=50 Hz。仿真信號()的時域波形如圖1所示,頻譜如圖2所示。
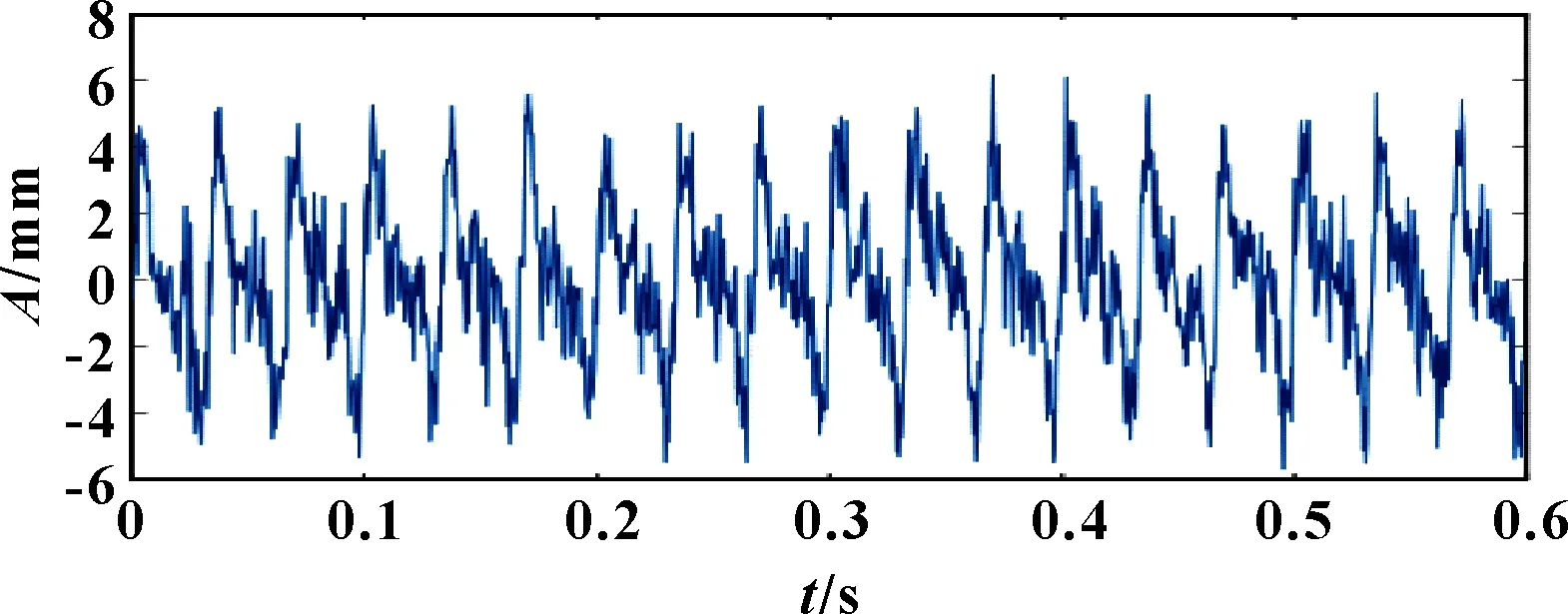
圖1 仿真信號X(t)的時域波形
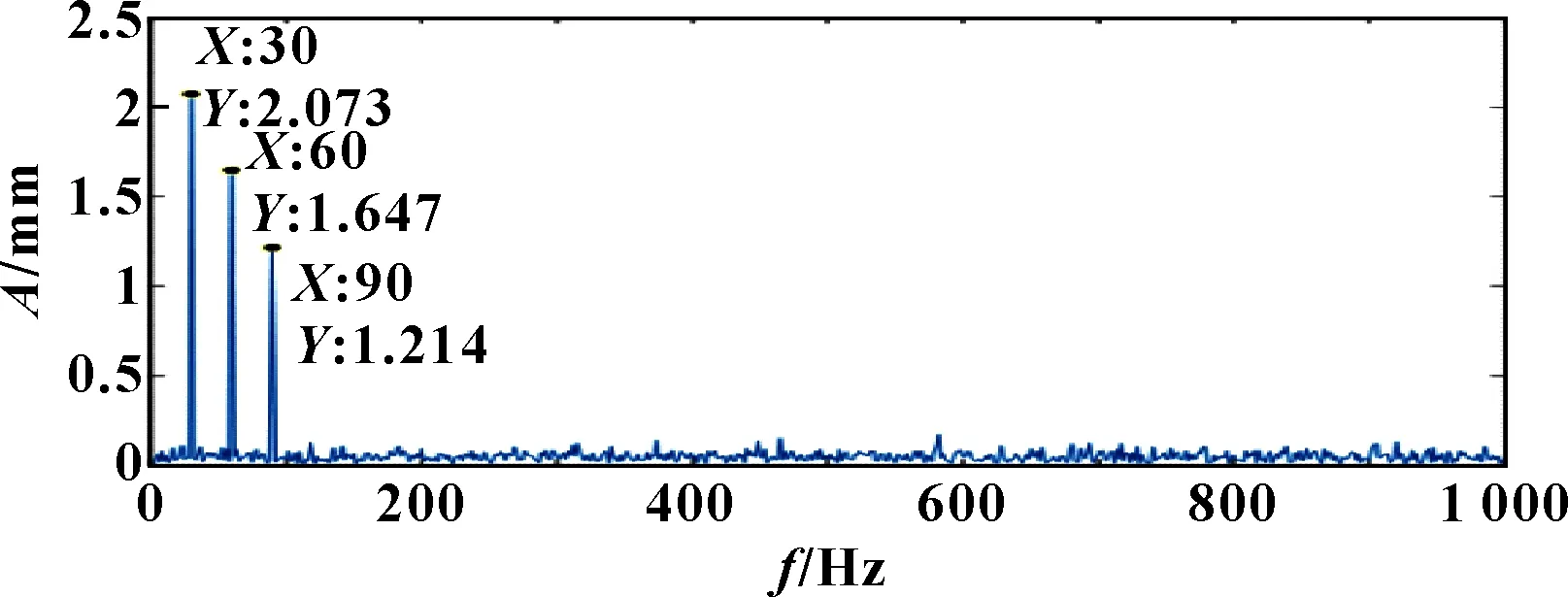
圖2 仿真信號X(t)的頻譜
構造大小為516×1 200的高斯觀測矩陣,對仿真信號進行降維處理,經式(2)得到大小為1×516的觀測信號。再構造大小為1 200×1 200的離散傅里葉變換字典與觀測矩陣相乘得到感知矩陣。基于感知矩陣,采用正交匹配追蹤算法對觀測信號()進行重構,得到稀疏系數的集合。根據式(12)分別計算出不同稀疏度時,重構信號()與仿真信號()的皮爾遜相關系數如表1所示。仿真信號()由3個主要分量組成,稀疏度取值應大于3。稀疏度越大,重構信號與仿真信號的相關性越強,當值大到一定程度時,相關性并無明顯提高,甚至會混入噪聲。根據實驗結果并考慮時效性,重構信號的稀疏度選取為6。=6時,重構信號()如圖3所示,其頻譜如圖4所示。
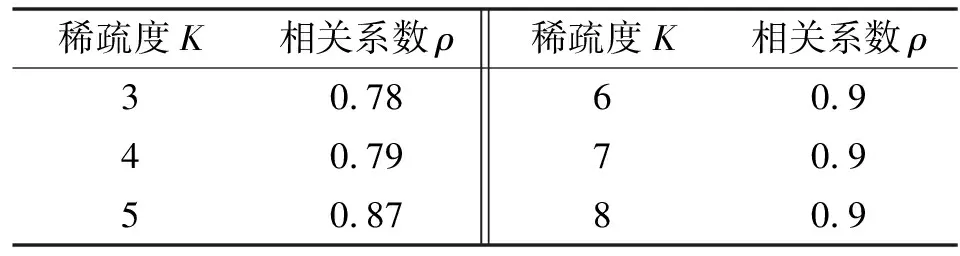
表1 稀疏度K
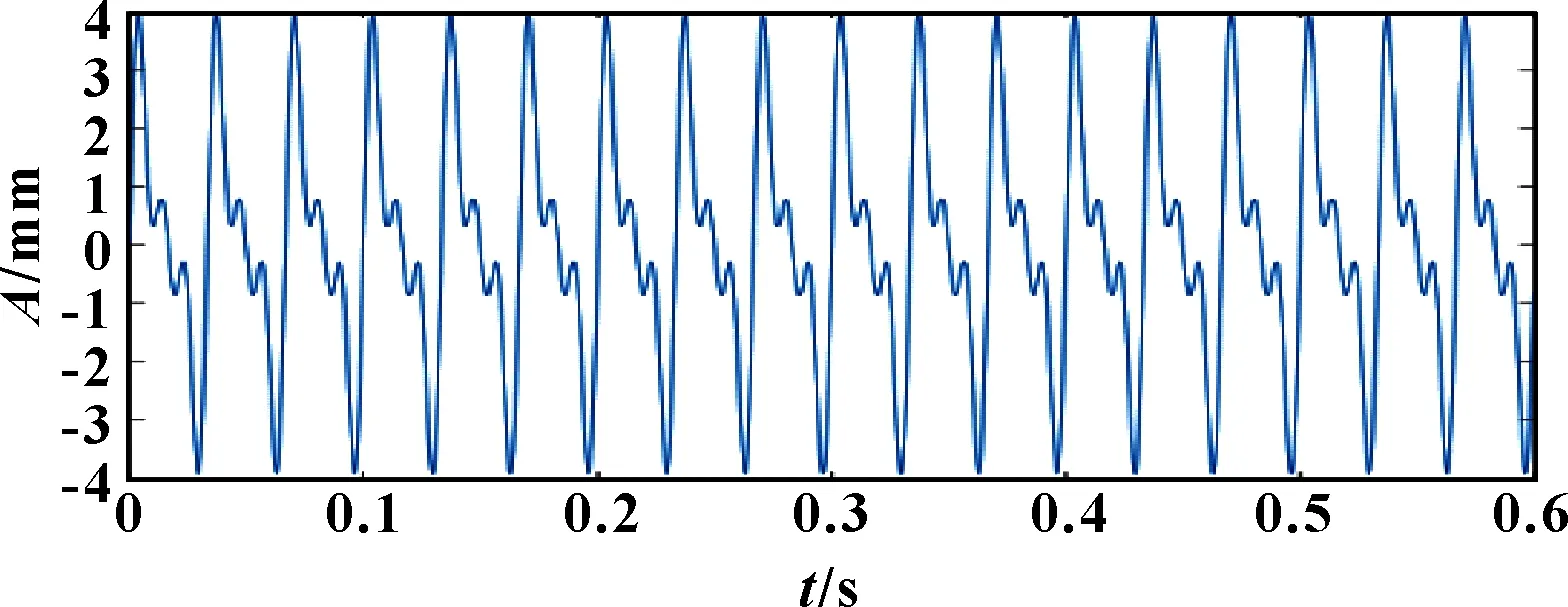
圖3 重構信號Sc(t)
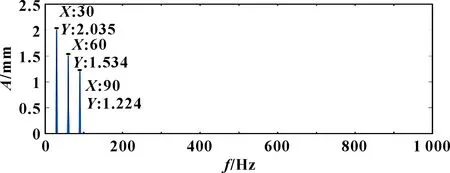
圖4 重構信號Sc(t)頻譜
由圖3、圖4可知:原始信號經重構后,噪聲和沖擊分量得到了有效抑制且重構信號保留了原始信號的大部分特征,譜峰與原始信號的譜峰誤差精確到0.01 Hz。現將稀疏系數中不為零的項與感知矩陣對應原子相乘,分離仿真信號不同的頻率成分。稀疏度=6時,稀疏分解結果如圖5—圖7所示。經MATLAB仿真計算,分離出的()~()與仿真信號()對應的轉頻、倍頻成分相關性均達到0.99。

圖5 稀疏分解信號Sc0(t)

圖6 稀疏分解信號Sc1(t)

圖7 稀疏分解信號Sc2(t)
3 轉子振動信號分析
3.1 軸承轉子實驗臺
實驗對象為Bently小型軸承轉子實驗臺,該實驗臺主要由驅動系統、控制系統、采集系統及機械結構等部分組成。為降低外界振動對軸承轉子系統的影響,在實驗平臺與軸承轉子系統之間增加具有良好減振性能的減振支座,最大程度地隔絕外界因素對實驗臺的干擾。Bently小型軸承轉子實驗臺如圖8所示,其中振動采集系統為LMS多功能數據采集器。

圖8 轉子實驗臺實物圖
3.2 轉頻和倍頻信號提取
使用LMS數據采集系統采集振動加速度信號,采樣頻率為16 384 Hz,轉速為4 000 r/min。其時域波形、頻譜及時頻圖分別如圖9—圖11所示。在4 000 r/min工況下,信號D1的轉頻為65.6 Hz,頻譜內存在高頻噪聲和轉子系統運行時激發的諧波分量。
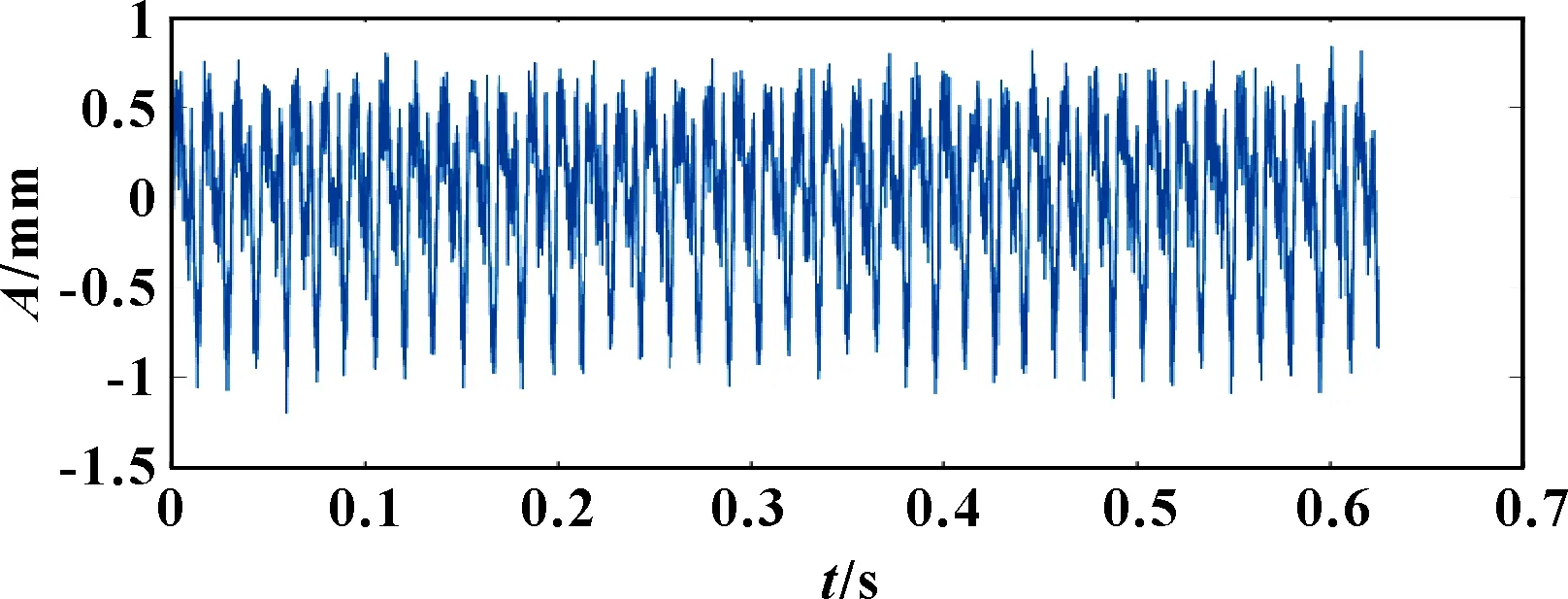
圖9 轉子振動信號D1時域波形
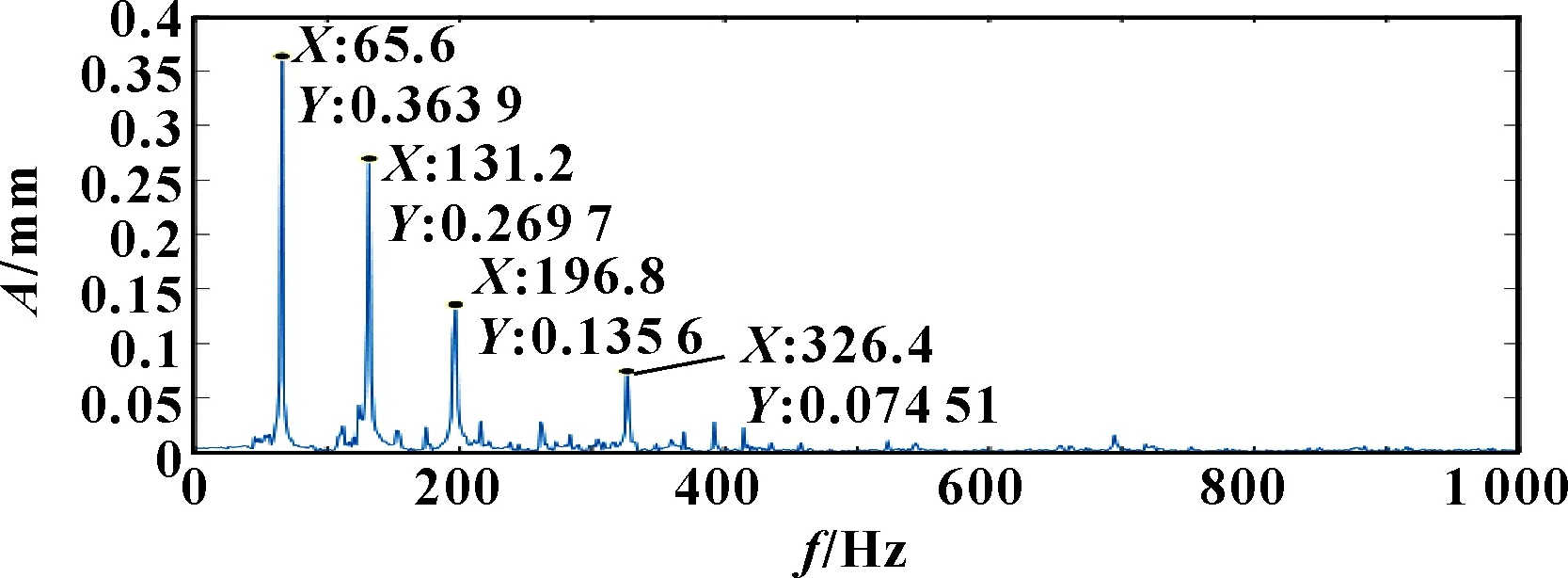
圖10 轉子振動信號D1頻譜
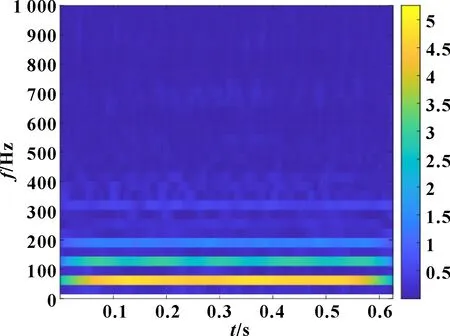
圖11 轉子振動信號D1小波時頻圖
由圖10可知:可以提取4個分量,分別為(65.6 Hz,0.363 9 mm)、(131.2 Hz,0.269 7 mm)、(196.8 Hz,0.135 6 mm)、(326.4 Hz,0.074 51 mm),濾除其余無用成分。
經MATLAB計算,當稀疏度=16時,重構信號與信號D1的相關系數為0.9,接近于1,相關性高。文中取=16對信號進行稀疏分解,結果如圖12—圖15所示。可以看出:文中方法準確地提取了轉子振動信號的轉頻及倍頻成分。
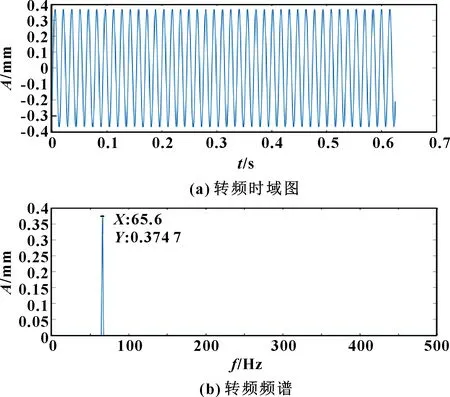
圖12 轉子轉頻
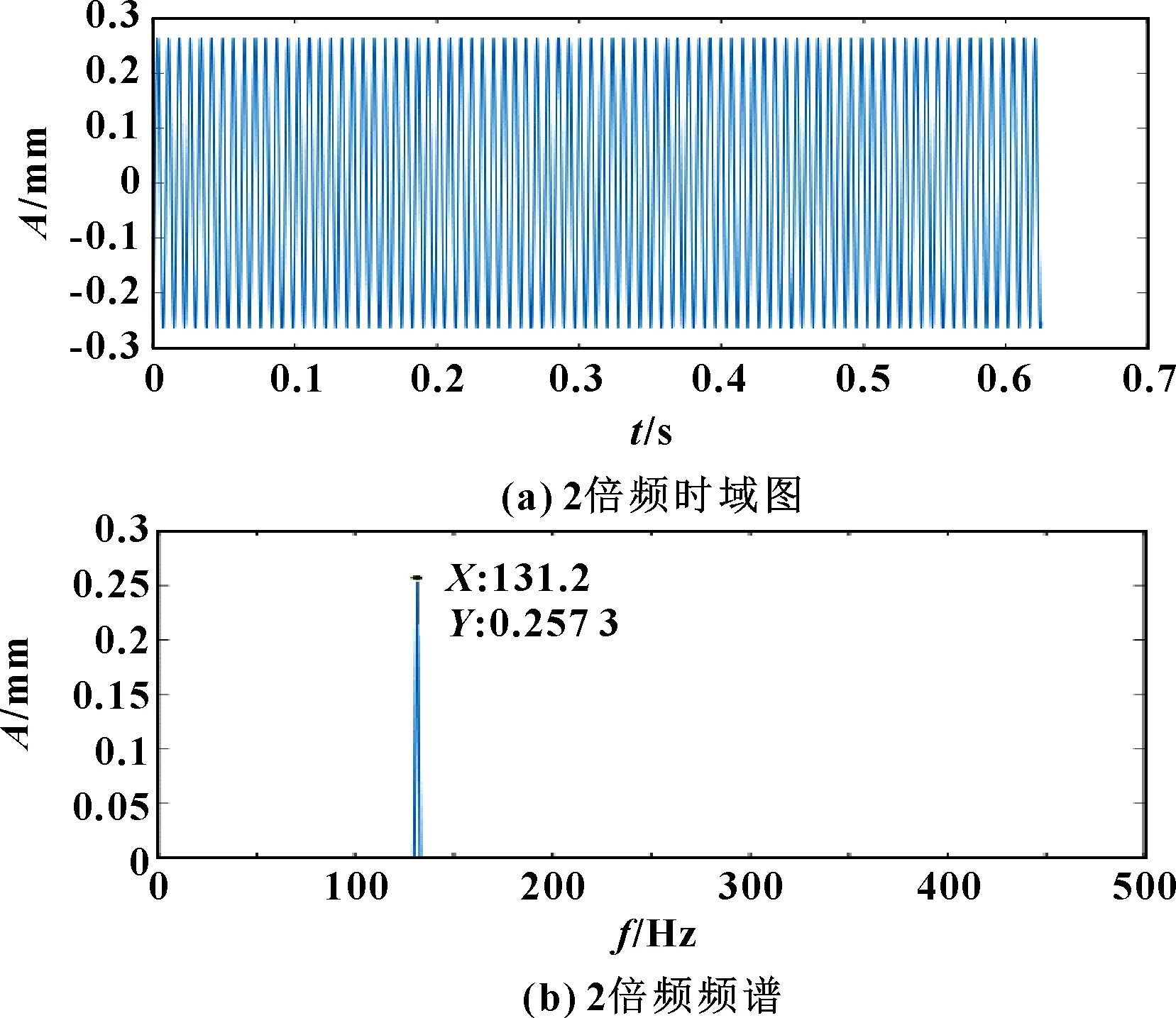
圖13 轉子2倍頻

圖14 轉子3倍頻
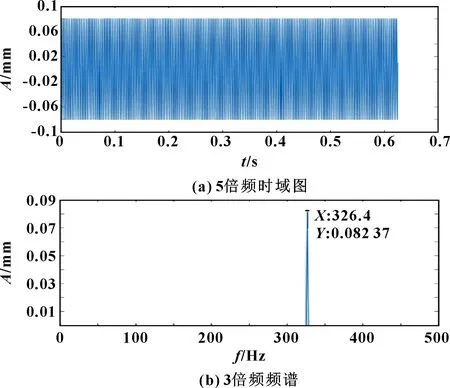
圖15 轉子5倍頻
以上實際工程應用證明文中方法的有效性和可行性,為轉子運行狀況監測和故障診斷提供純凈的信號,有利于進一步信號分析。
4 結論
為解決傳統信號處理方法難以對含噪混疊信號進行分析的難點,本文作者提出互相關稀疏分解法。利用該方法對信號采用壓縮感知,僅需少量數據就可以保留信號的大部分特征,用遠低于奈奎斯特采樣定理要求的采樣頻率完成信號的重建恢復,進而引出稀疏度對重構信號的影響。稀疏度過大,重構信號的噪聲分量會增加,過小,重構信號會丟失特征信息。因此,需選擇最合適的稀疏度完成對仿真信號的降噪重構。
為了驗證該方法的可行性,首先利用皮爾遜系數計算稀疏分解后的信號與原信號的相關性,并通過計算相關系數來解決稀疏度的取值問題。當稀疏分解的信號與原信號相關性好(>0.7)時,保留該信號。將稀疏系數與字典中對應的原子相乘,分離出仿真信號中不同的頻率成分,最后對轉子振動信號實例進行分析,成功提取轉子的轉頻及其倍頻成分。仿真實驗結果驗證了該方法的有效性和可行性,可為轉子運行狀況監測和故障診斷提供純凈的信號,有利于進一步分析信號。結果表明:與傳統的信號處理方法相比,用互相關稀疏分解法處理的旋轉機械運行的含噪混疊信號更易于分析,有助于旋轉機械的運行狀況監測和故障診斷。

