永磁同步電機位置伺服系統終端滑模控制
岳陸游,湯少東,張兵
(江蘇大學機械工程學院,江蘇鎮江 212013)
0 前言
永磁同步電機(Permanent Magnet Synchronous Motor,PMSM)由于體積小、結構簡單、工作時效率高等優點,被廣泛應用于轉臺、機器人、半導體裝備、工廠自動化、醫療設備以及軍工等高性能伺服系統。在永磁同步電機的控制方法中,通常使用的是經典的PID控制,但由于永磁同步電機是強耦合、非線性系統,具有多種干擾和參數變化,導致傳統的PID控制很難滿足現代工業不斷增長的控制性能需求。為減少這些因素帶來的影響,研究更好的控制方法和干擾補償策略顯得尤為重要。
為提高永磁同步電機伺服系統的位置跟蹤性能,國內外學者進行了很多工作,也提出了很多解決辦法。文獻[1]提出了一種自適應滑模控制器,用于永磁同步電機的位置跟蹤控制,自適應控制被用來在線估計未知參數和切換增益的界限以提高控制性能。文獻[2]為了衰減在真實應用中不需要的抖動可能對機械系統造成影響,采用飽和功能替換符號功能,有效地衰減抖動。文獻[3]采用模糊PI控制方法,對永磁同步電機位置伺服系統進行位置跟蹤,有效減少了超調,同時也抑制了振蕩。文獻[4]針對參數變化,將自適應與模糊反演控制算法相結合,保證了位置誤差在一個比較小的范圍內波動。文獻[5]采用模塊化的神經動態表面控制方法,改善了永磁同步電機位置跟蹤瞬態性能。文獻[6]提出了一種自組織模糊滑模控制器,提高了永磁同步電機位置伺服系統的性能和魯棒性。文獻[7]設計了一種具有快速滑動表面和連續達到律的滑模控制器,提高了永磁同步電機的控制性能,實現了位置控制的快速響應。
本文作者針對永磁同步電機位置伺服系統中存在的外部負載干擾和系統內部參數攝動,設計一種基于干擾觀測器的終端滑模控制方法(Terminal Sliding Mode Control,TSMC)。設計終端滑模干擾觀測器,對干擾進行估計,并將估計值引入滑模控制中進行補償,提高系統的抗干擾能力。采用終端滑模控制方法對滑模位置進行跟蹤,保證系統在有限時間內達到穩定狀態并且收斂,提高系統響應速度和位置跟蹤精度。
1 永磁同步電機的數學模型
考慮到永磁同步電機是一個強耦合、復雜的非線性系統,為簡化分析,作如下假設:(1)不計渦流和磁帶損耗;(2)氣息磁場呈正弦分布;(3)忽略鐵心的飽和效應。
以表貼式永磁同步電機為例(==),在d-q坐標系下,可得如下數學模型:
電壓方程為

(1)
其中:=+;=。
電機機械運動方程為

(2)

=3/2[-(-)]
(3)
又因為==,則PMSM的電磁轉矩可以重新寫成:
=3/2=
(4)
式中:=3/2,=作為控制的輸入。
考慮到非線性摩擦,給出如下非線性摩擦模型:

(5)
式中:為庫侖摩擦力矩;為最大靜摩擦力矩;為黏性摩擦力矩比例系數;?為一個比較小的正數。

然后,考慮到參數不確定性,模型[式(2)]可以寫為

(6)


(7)

假設1:由參數不確定性和未知的外部負載引起集成的不確定擾動是有界的,即||<,是已知的。
2 有限時間收斂的干擾觀測器設計
引理1:假設存在滿足以下不等式的連續正定函數():

(8)
那么()收斂到平衡點的有限時間為
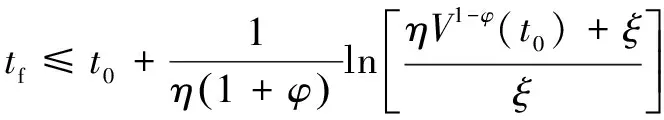
(9)
其中:、>0;0<<1;為關于的初始時間。
為設計具有有限時間收斂的滑模干擾觀察器,引入以下輔助變量:
=-
(10)
為保證有限時間收斂,定義滿足以下形式:

(11)
式中:和為正的奇數,并且<;、、為正數。
那么終端滑動模式干擾估計為

(12)
引理2:考慮公式(11)和公式(7),在假設1的前提下,如果||<,那么干擾觀測器能夠確保在有限時間內收斂。
證明:
考慮以下Lyapunov函數:
=12
(13)
對式(13)求導可得:


sign()-(+)-≤--||-(+)+
||||≤--(+)≤--()(+)(2)≤
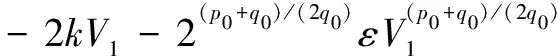
(14)
根據引理1,輔助變量能夠在有限時間內收斂到平衡點。另外,可得觀測誤差為


(15)

3 終端滑模控制器設計
定義1:對于考慮任意高階的單輸入單輸出非線性系統:

(16)
其中:=[…,]為系統可測量的狀態;()和()為域內的光滑函數;∈為系統的輸入;為系統干擾。
那么可以得到一種具有遞歸結構的終端滑動模態為

(17)
式中:(=1,2,…,)為次終端滑模面;>0、>0;和為正奇數(=1,2,…,-1)。
考慮系統的位置控制,定義位置誤差為
=-
(18)
則的二階導數為

(19)
為實現PMSM的有限時間位置跟蹤,滑動模式表面設計如下:
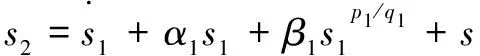
(20)
其中:==-。
由式(20)可得的導數為
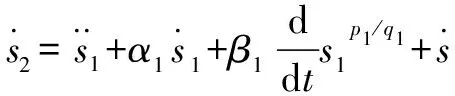
(21)
考慮式(7)(19),可得:

那么,基于干擾觀測器的終端滑動模式跟蹤控制可設計為

(22)
其中:、>0。
考慮到非線性系統[式(7)]和終端滑動模式干擾觀察器[式(10)—(12)],在終端滑動模式跟蹤控制[式(22)]下,閉環系統的所有信號都在有限時間內收斂。
證明:
把式(22)代入式(21),可得:

(23)
又根據式(15)可得:

(24)
考慮Lyapunov函數:
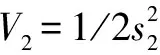
(25)
由式(14)(24)可得:


(26)
根據定理1,可以知道滑動模態變量是有限時間收斂的;從公式(20)可得是和的函數;根據引理2,可以得到是有限時間收斂的,所以可以得到是有限時間收斂的,因此閉環系統的所有信號都會在有限時間收斂到平衡點。
綜上所述,永磁同步電機終端滑模控制方案的框圖如圖1所示。

圖1 永磁同步電機終端滑模控制框圖
4 仿真和討論
基于MATLAB/Simulink平臺對該控制算法進行仿真驗證,仿真時所使用的永磁同步電機的部分參數如表1所示。

表1 PMSM的參數
干擾觀測器參數:=2 500,=30,=01,=5,=9。摩擦參數:=1 N·m;=0.8 N·m;?=2,=0.000 3 N·m·s/rad。控制器參數:=30,=60,=5,=7,=30,=50,=5,=7。為進行比較,證明終端滑動模式控制的有效性,PID控制、傳統的反演法控制(Traditional Backstepping Control,TBC)也被應用于PMSM。
(1)PID控制

其中:=1 500,=0.5,=0.05。
(2)傳統的反演法控制(TBC)
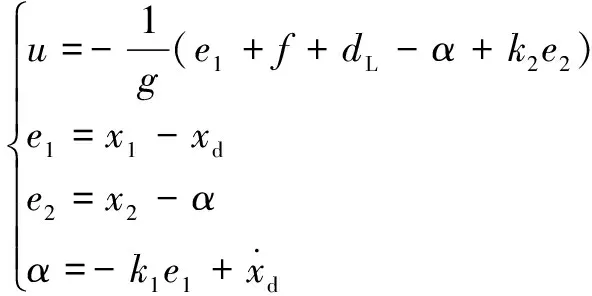
其中:為的參考值;=60;=60。
2種位置參考給定為


2種不確定干擾給定為
=2sin(2π)=3+sin(π)
由圖2—圖5可知:在2種不同位置參考下,3種控制器都可以保證位置跟蹤。由圖3可知:當給定外部干擾為、位置參考為時,TBC穩態時產生了1.4%的最大跟蹤誤差,PID更是達到了1.6%,而TSMC的跟蹤誤差幾乎為0。由圖5可知:當給定外部干擾為、位置參考為時,TBC穩態時最大跟蹤誤差為1.5%,PID跟蹤效果最差,誤差達到2.3%,而TSMC穩態時的跟蹤誤差幾乎為0。通過對比2種不同位置參考下3種控制器的跟蹤結果,可以得到TSMC無論是控制精度還是響應速度都優于TBC和PID,驗證了終端滑動模式控制的有效性。

圖2 施加干擾dL1,位置參考為y1時,3種控制器的位置跟蹤曲線

圖3 施加干擾dL1,位置參考為y1時,3種控制器的跟蹤誤差

圖4 施加干擾dL2,位置參考為y2時,3種控制器的位置跟蹤

圖5 施加干擾dL2,位置參考為y2時,3種控制器的跟蹤誤差
5 結論
本文作者基于PMSM位置控制回路的嚴格反饋非線性模型,提出終端滑模控制策略。對于不確定擾動,設計一種新的干擾觀測器對干擾進行估計并補償。結果表明:所提出的控制策略具有更快的響應速度和更好的跟蹤性能。

